Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-23T01:23:43.978Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed ƒ-divergence for Multiple Pairs of Measures

Published online by Cambridge University Press:  20 November 2018

Elisabeth Werner  and
Deping Ye
Elisabeth Werner
Affiliation:
Department of Mathematics, Case Western Reserve University, Cleveland, Ohio 100, USA e-mail: [email protected]
Deping Ye
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St. John's, Newfoundland A1C SS7 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, the concept of the classical 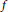$f$-divergence for a pair of measures is extended to the mixed 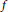$f$-divergence formultiple pairs ofmeasures. The mixed 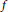$f$-divergence provides a way to measure the difference between multiple pairs of (probability) measures. Properties for the mixed 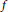$f$-divergence are established, such as permutation invariance and symmetry in distributions. An Alexandrov–Fenchel type inequality and an isoperimetric inequality for the mixed 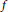$f$-divergence are proved.

Keywords

28-XX52-XX60-XXAlexandrov–Fenchel inequalityƒ-dissimilarityƒ-divergenceisoperimetric inequality
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 3 , 01 September 2017 , pp. 641 - 654
Copyright
Copyright © Canadian Mathematical Society 2017

References

[1] Aleksandrov, A. D., On the theory of mixed volumes of convex bodies. II. New inequalities between mixed volumes and their applications. (Russian) Mat. Sb. (N. S.) 2(1937), 1205–1238. Google Scholar
[2] Ali, S. M. and Silvey, D., A general class of coefficients of divergence of one distribution from another. J. Roy. Statist. Soc. Ser. B 28(1966), 131–142. Google Scholar
[3] Barron, A. R., L. Gyorfi, and van der Meulen, E. C., Distribution estimates consistent in total variation and two types of information divergence. IEEE Trans. Inform. Theory 38(1990), 1437–1454. Google Scholar
[4] Basseville, M., Divergence measures for statistical data processing. Technical Report PI 1961, IRISA, November 2010. http://hal.inria.fr/inria-OO542337/fr/ Google Scholar
[5] Bhattacharyya, A., On some analogues to the amount of information and their uses in statistical estimation. Sankhya 8(1946), 1–14. Google Scholar
[6] Busemann, H., Convex surfaces. Interscience Tracts in Pure and Applied Mathematics, 6, Interscience, London, 1958.Google Scholar
[7] Cover, T. and Thomas, J., Elements of information theory, second ed., Wiley-Interscience, (John Wiley and Sons), Hoboken, NJ, 2006. Google Scholar
[8] Csiszar, I., Eine informationstheoretische Ungleichung und ihre Anwendung aufden Beweis der Ergodizitat von Markoffschen Ketten. Magyar Tud. Akad. Mat. Kutato Int. Kozl. 8(1963), 85–108. Google Scholar
[9] Gardner, R. J., The Brunn-Minkowski Inequality. Bull. Amer. Math. Soc. 39(2002), no. 3, 355–405 . http://dx.doi.Org/10.1090/S0273-0979-02-00941-2 Google Scholar
[10] Guleryuz, O. G., Lutwak, E., Yang, D., and Zhang, G., Information theoretic inequalities for contoured probability distributions. IEEE Trans. Inform. Theory 48(2002), 2377–2383. http://dx.doi.Org/10.1109/TIT.2002.800496 Google Scholar
[11] Gyorfi, L. and Nemetz, T., f-dissimilarity: A general class of separation measures of several probability measures. In: Topics in information theory, Colloquia Mathematica Societatis Janos Bolyai, 16, North-Holland, 1975, pp. 309–321.Google Scholar
[12] Gyorfi, L. and Nemetz, T., f-dissimilarity: A generalization of the affinity of several distributions. Ann. Inst. Statist. Math. 30(1978), 105–113. http://dx.doi.Org/10.1007/BF02480206 Google Scholar
[13] Hardy, G. H., Littlewood, J. E., and Polya, G., Inequalities, second ed., Cambridge University Press, Cambridge, 1952. Google Scholar
[14] Harremoes, P. and Topsoe, F., Inequalities between entropy and the index of coincidence derived from information diagrams. IEEE Trans. Inform. Theory 47(2001), no. 7, 2944–2960. http://dx.doi.Org/10.1109/18.9592 72 Google Scholar
[15] Jenkinson, J. and Werner, E., Relative entropies for convex bodies. Trans. Amer. Math. Soc. 366(2014), no. 6, 2889–2906. http://dx.doi.Org/10.1090/S0002-9947-2014-05788-7 Google Scholar
[16] Kullback, S. and Leibler, R. A., On information and sufficiency. Ann. Math. Statistics 22(1951), 79–86. http://dx.doi.Org/10.1214/aoms/117772 9694 Google Scholar
[17] Liese, F. and Vajda, I., On divergences and information in statistics and information theory. IEEE Trans. Inform. Theory 52(2006), 4394–4412. http://dx.doi.Org/10.1109/TIT.2006.881731 Google Scholar
[18] Ludwig, M., General affine surface areas. Adv. Math. 224(2010), no. 6, 2346–2360. http://dx.doi.Org/10.1016/j.aim.2O10.02.004 Google Scholar
[19] Ludwig, M. and Reitzner, M., A characterization of affine surface area. Adv. Math. 147(1999), no. 1, 138–172. http://dx.doi.Org/10.1 006/aima.1 999.1 832 Google Scholar
[20] Ludwig, M. and Reitzner, M., A classification ofSL(n) invariant valuations. Annals of Math. 172(2010), no. 2, 1223–1271. http://dx.doi.Org/10.4007/annals.201 0.1 72.1 223 Google Scholar
[21] Lutwak, E., Mixed affine surface area. J. Math. Anal. Appl. 125(1987), no. 2, 351–360. http://dx.doi.Org/1 0.101 6/0022-247X(87)90097-7 Google Scholar
[22] Lutwak, E., The Brunn-Minkowski-Firey theory. II. affine and geominimal surface areas. Adv. Math. 118(1996), no. 2, 244–294. http://dx.doi.Org/10.1006/aima.1996.0022 Google Scholar
[23] Lutwak, E., Yang, D., and Zhang, G., The Cramer-Rao inequality for star bodies. Duke Math. J. 112(2002), 59–81. http://dx.doi.Org/10.1215/S0012-9074-02-11212-5 Google Scholar
[24] Lutwak, E., Yang, D., and Zhang, G., Moment-entropy inequalities. Ann. Probab. 32(2004), 757–774. http://dx.doi.Org/10.1214/aop/1079021463 Google Scholar
[25] Lutwak, E., Yang, D., and Zhang, G., Cramer-Rao and moment-entropy inequalities for Renyi entropy and generalized Fisher information. IEEE Trans. Inform. Theory 51(2005), 473–478. http://dx.doi.Org/1 0.1109/TIT.2004.840871 Google Scholar
[26] Matusita, K., On the notion of affinity of several distributions and some of its applications. Ann. Inst. Statist. Math. 19(1967), 181–192. http://dx.doi.Org/10.1007/BF02911 675 Google Scholar
[27] Matusita, K., Some properties of affinity and applications. Ann. Inst. Statist. Math. 23(1971), 137–155. http://dx.doi.Org/10.1007/BF02479219 Google Scholar
[28] Menendez, M. L., Pardo, J. A., Pardo, L., and Zografos, K., A preliminary test in classification and probabilities of misclassification. Statistics 39(2005), 183–205. http://dx.doi.Org/10.1080/02331880500097986 Google Scholar
[29] Morales, D., Pardo, L., and Zografos, K., Informational distances and related statistics in mixed continuous and categorical variables. J. Statist. Plann. Inference 75(1998), 47–63. http://dx.doi.Org/1 0.101 6/S0378-3758(98)00120-7 Google Scholar
[30] Morimoto, T., Markov processes and the H-theorem. J. Phys. Soc. Jap. 18(1963), 328–331. http://dx.doi.Org/10.1143/JPSJ.18.328 Google Scholar
[31] Osterreicher, F. and Vajda, I., A new class of metric divergences on probability spaces and its applicability in statistics. Ann. Inst. Statist. Math. 55(2003), 639–653. http://dx.doi.Org/10.1007/BF02517812 Google Scholar
[32] Paouris, G. and Werner, E., Relative entropy of cone measures and Lp centroid bodies. Proc. London Math. Soc. 104(2012), 253–286. http://dx.doi.Org/!0.1112/plms/pdrO3O Google Scholar
[33] Schneider, R., Convex bodies: the Brunn-Minkowski theory. Cambridge University Press, Cambridge, 1993. http://dx.doi.Org/10.1017/CBO9780511526282 Google Scholar
[34] Schiitt, C. and Werner, E., Surface bodies andp-affme surface area. Adv. Math. 187(2004), no. 1, 98–145. http://dx.doi.Org/10.1016/j.aim.2003.07.018 Google Scholar
[35] Sgarro, A., Informational divergence and the dissimilarity of probability distributions. Calcolo 18(1981), 293–302. http://dx.doi.Org/10.1007/BF02576360 Google Scholar
[36] Sibson, R., Information radius. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 14(1969), 149–160. http://dx.doi.Org/10.1007/BF00537520 Google Scholar
[37] Toussaint, G. T., Some properties of Matusita's measure of affinity of several distributions. Ann. Inst. Statist. Math. 26(1974), 389–394. http://dx.doi.Org/10.1007/BF02479834 Google Scholar
[38] Werner, E., Renyi Divergence and Lp-affine surface area for convex bodies. Adv. Math. 230(2012), 1040–1059. http://dx.doi.Org/10.101 6/j.aim.2O12.03.01 5 Google Scholar
[39] Werner, E., f-Divergence for convex bodies. Proceedings of the “Asymptotic Geometric Analysis“ workshop, Fields Inst. Commun, Springer, New York, 2012, pp. 381–395. http://dx.doi.Org/10.1007/978-1-4614-6406-8J8 Google Scholar
[40] Werner, E. and Ye, D., Inequalities for mixed p-affine surface area. Math. Ann. 347(2010), 703–737. http://dx.doi.Org/1 0.1007/S00208-009-0453-2 Google Scholar
[41] Ye, D., Inequalities for general mixed affine surface areas. J. London Math. Soc. 85(2012), 101–120. http://dx.doi.Org/1 0.1112/jlms/jdrO43 Google Scholar
[42] Zografos, K., f-dissimilarity of several distributions in testing statistical hypotheses. Ann. Inst. Statist. Math. 50(1998), 295–310. http://dx.doi.Org/10.1023/A:1003443215838 Google Scholar