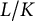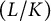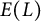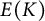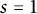1 Introduction
Let E be an elliptic curve defined over a number field K, and let
![]() $L/K$
be a finite Galois extension with Galois group
$L/K$
be a finite Galois extension with Galois group
![]() $G=$
Gal
$G=$
Gal
![]() $(L/K)$
. The famous Mordell–Weil Theorem tells us that,
$(L/K)$
. The famous Mordell–Weil Theorem tells us that,
![]() $E(L)$
, the group of L-rational points of E, is finitely generated. Throughout this paper, we will focus on the “free part” of the Mordell–Weil group, that is,
$E(L)$
, the group of L-rational points of E, is finitely generated. Throughout this paper, we will focus on the “free part” of the Mordell–Weil group, that is,
![]() $E(L)$
modulo the torsion subgroup
$E(L)$
modulo the torsion subgroup
![]() $E(L)_{\text {tors}}$
and denote the rank of this quotient by
$E(L)_{\text {tors}}$
and denote the rank of this quotient by
![]() ${\mathbf {rk}} E(L)$
. The question of studying this free part of
${\mathbf {rk}} E(L)$
. The question of studying this free part of
![]() $E(L)$
as a
$E(L)$
as a
![]() ${\mathbb Z}[G]$
-module is an appealing one and was raised in the works of Mazur and Swinnerton-Dyer [Reference Mazur and Swinnerton-Dyer19], Coates and Wiles [Reference Coates and Wiles4], and others. Toward this study, Akbary and Murty in [Reference Akbary and Kumar Murty1] introduced the idea of a minimal subfield:
${\mathbb Z}[G]$
-module is an appealing one and was raised in the works of Mazur and Swinnerton-Dyer [Reference Mazur and Swinnerton-Dyer19], Coates and Wiles [Reference Coates and Wiles4], and others. Toward this study, Akbary and Murty in [Reference Akbary and Kumar Murty1] introduced the idea of a minimal subfield:
![]() $M \subseteq L$
, minimal, such that
$M \subseteq L$
, minimal, such that
![]() $ {\mathbf {rk}} E(M) = {\mathbf {rk}} E(L)$
and produced explicit examples. They gave a description of the possibilities for Gal
$ {\mathbf {rk}} E(M) = {\mathbf {rk}} E(L)$
and produced explicit examples. They gave a description of the possibilities for Gal
![]() $(M/K)$
when the rank
$(M/K)$
when the rank
![]() $E(L)$
is small (e.g., 1, 2, and 3). In the first part of this paper, we generalize their results from small rank to small increase in rank. We show that similar descriptions of Gal
$E(L)$
is small (e.g., 1, 2, and 3). In the first part of this paper, we generalize their results from small rank to small increase in rank. We show that similar descriptions of Gal
![]() $(M/K)$
holds when
$(M/K)$
holds when
![]() ${\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
for
${\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
for
![]() $t=1,2,$
and
$t=1,2,$
and
![]() $3$
. We prove the following theorem.
$3$
. We prove the following theorem.
Theorem 1.1 Let
![]() $L/K$
be a Galois extension of number fields, and let
$L/K$
be a Galois extension of number fields, and let
![]() $E/K$
be an elliptic curve such that
$E/K$
be an elliptic curve such that
![]() $\; {\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
. Let M be the minimal subfield.
$\; {\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
. Let M be the minimal subfield.
-
(1) If
 $t=1$
, then M is a quadratic extension of K.
$t=1$
, then M is a quadratic extension of K. -
(2) If
 $t=2$
, then M is either a cyclic extension of K with
$t=2$
, then M is either a cyclic extension of K with
 $[M:K] = 2,3,4,6$
or a dihedral extension of K with
$[M:K] = 2,3,4,6$
or a dihedral extension of K with
 $[M:K] = 4,6,8,12$
.
$[M:K] = 4,6,8,12$
. -
(3) If
 $t=3$
, then
$t=3$
, then
 ${\mathrm{Gal}}(M/K)$
is isomorphic to one of the following:
${\mathrm{Gal}}(M/K)$
is isomorphic to one of the following:-
 $C_n \times C_m, $
where
$C_n \times C_m, $
where
 $ n=2,3,4 $
and
$ n=2,3,4 $
and
 $ m=1,2,$
$ m=1,2,$
-
 $D_{2p} \times C_m,$
where
$D_{2p} \times C_m,$
where
 $ p=2, 3, 4, 6 $
and
$ p=2, 3, 4, 6 $
and
 $ m=1,2,$
$ m=1,2,$
-
 $ A_4 \times C_m, \;\;$
or
$ A_4 \times C_m, \;\;$
or
 $ \;S_4 \times C_m $
where
$ \;S_4 \times C_m $
where
 $m=1,2.$
$m=1,2.$
-
Section 2 is largely devoted to proving the above theorem starting with a precise definition of the minimal subfield.
We then venture on a more analytic side of things. The famous Birch and Swinnerton-Dyer conjecture connects the rank of an elliptic curve to the order of vanishing of its L-function at
![]() $s=1$
. In this regard, Akbary and Murty introduced the analytic notion of the minimal subfield in [Reference Akbary and Kumar Murty1]. Its existence is dependent on the holomorphy of
$s=1$
. In this regard, Akbary and Murty introduced the analytic notion of the minimal subfield in [Reference Akbary and Kumar Murty1]. Its existence is dependent on the holomorphy of
![]() $L(E/K \otimes \chi , s)$
for irreducible characters
$L(E/K \otimes \chi , s)$
for irreducible characters
![]() $\chi $
of the Galois group. For number fields, classical theorems of Foote–Murty and Foote–Wales, shows holomorphy of Artin L-functions when the Dedekind zeta function has a zero of small order. In Sections 4 and 5, we develop elliptic analogues of these theorems. For example, we show the following.
$\chi $
of the Galois group. For number fields, classical theorems of Foote–Murty and Foote–Wales, shows holomorphy of Artin L-functions when the Dedekind zeta function has a zero of small order. In Sections 4 and 5, we develop elliptic analogues of these theorems. For example, we show the following.
Theorem 1.2 Let
![]() $E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
$E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
![]() $G=\mathrm{Gal}(F/K)$
. Let
$G=\mathrm{Gal}(F/K)$
. Let
![]() $\chi $
be an irreducible character of G. Then
$\chi $
be an irreducible character of G. Then
![]() $L(E/K \otimes \chi , s)$
is holomorphic at
$L(E/K \otimes \chi , s)$
is holomorphic at
![]() $s = \omega $
, if
$s = \omega $
, if
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F, s)$
of order
$L(E/F, s)$
of order
![]() $r \leq p_2 - 2$
, where
$r \leq p_2 - 2$
, where
![]() $p_2$
is the second smallest prime factor of
$p_2$
is the second smallest prime factor of
![]() $|G|$
.
$|G|$
.
We also prove that Theorem 1.2 holds for
![]() $r=2$
. These results establish existence of the analytic minimal subfield when the L-function of E over the top field has a zero of small order. Also note that these results are unconditional if we assume
$r=2$
. These results establish existence of the analytic minimal subfield when the L-function of E over the top field has a zero of small order. Also note that these results are unconditional if we assume
![]() $K = {\mathbb Q}$
as modularity is known. In Section 6, similar to the algebraic case, we investigate the possibilities of the Galois group for the analytic minimal subfield, when the order of vanishing at
$K = {\mathbb Q}$
as modularity is known. In Section 6, similar to the algebraic case, we investigate the possibilities of the Galois group for the analytic minimal subfield, when the order of vanishing at
![]() $s=1$
of
$s=1$
of
![]() $L(E/F, s)$
is 2. As an application, we show the following slight generalization of a theorem of Kolyvagin.
$L(E/F, s)$
is 2. As an application, we show the following slight generalization of a theorem of Kolyvagin.
Theorem 1.3 Let
![]() $E/{\mathbb Q}$
be an elliptic curve, and let
$E/{\mathbb Q}$
be an elliptic curve, and let
![]() $K/{\mathbb Q}$
be a solvable Galois extension.
$K/{\mathbb Q}$
be a solvable Galois extension.
-
(i) If
 ${\mathbf {rk}} E(K)$
=
${\mathbf {rk}} E(K)$
=
 ${\mathbf {rk}} E({\mathbb Q}) + 1$
, then ord
${\mathbf {rk}} E({\mathbb Q}) + 1$
, then ord
 $_{s=1} \; L(E/K,s) \geq $
ord
$_{s=1} \; L(E/K,s) \geq $
ord
 $_{s=1} \; L(E/{\mathbb Q},s) + 1$
.
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
. -
(ii) If
 $L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
$L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
 $s=1$
, for every irreducible character
$s=1$
, for every irreducible character
 $\chi $
of
$\chi $
of
 $\mathrm{Gal}(K/{\mathbb Q})$
and ord
$\mathrm{Gal}(K/{\mathbb Q})$
and ord
 $_{s=1} \; L(E/K,s) = $
ord
$_{s=1} \; L(E/K,s) = $
ord
 $_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
 ${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
In both cases, equality holds if the algebraic and the analytic minimal subfields are equal.
We also show that the holomorphy condition in Theorem 1.3(ii) can be dropped if E has CM.
1.1 Notation and terminology
We will be using a fair bit of group theory and representation theory of finite groups. In this subsection, we briefly introduce the notations and terminologies we have used.
Throughout the paper,
![]() $C_n$
is the cyclic group of order n,
$C_n$
is the cyclic group of order n,
![]() $D_{2n}$
is the dihedral group of order
$D_{2n}$
is the dihedral group of order
![]() $2n$
,
$2n$
,
![]() $Q_8$
is the quaternion group of order
$Q_8$
is the quaternion group of order
![]() $8$
, whereas,
$8$
, whereas,
![]() $S_n$
and
$S_n$
and
![]() $A_n$
are, respectively, the symmetric and the alternating group of n symbols. If V is a vector space, then by
$A_n$
are, respectively, the symmetric and the alternating group of n symbols. If V is a vector space, then by
![]() $\operatorname {\mathrm {GL}}(V)$
, we denote the group of automorphisms of V. By
$\operatorname {\mathrm {GL}}(V)$
, we denote the group of automorphisms of V. By
![]() $\operatorname {\mathrm {GL}}_n(K)$
(resp.
$\operatorname {\mathrm {GL}}_n(K)$
(resp.
![]() $\operatorname {\mathrm {SL}}_n(K)$
), we denote the group of
$\operatorname {\mathrm {SL}}_n(K)$
), we denote the group of
![]() $n \times n$
invertible matrices (resp. matrices with determinant
$n \times n$
invertible matrices (resp. matrices with determinant
![]() $1$
) with entries in K. When
$1$
) with entries in K. When
![]() $K = \mathbb {F}_q$
, a finite field with q elements, we have simply written it as
$K = \mathbb {F}_q$
, a finite field with q elements, we have simply written it as
![]() $\operatorname {\mathrm {GL}}_n(q)$
(resp.
$\operatorname {\mathrm {GL}}_n(q)$
(resp.
![]() $\operatorname {\mathrm {SL}}_n(q)$
). We have used PGL
$\operatorname {\mathrm {SL}}_n(q)$
). We have used PGL
![]() $_n(K)$
for the projective general linear group, defined as
$_n(K)$
for the projective general linear group, defined as
![]() $\operatorname {\mathrm {GL}}_n(K) / Z(\operatorname {\mathrm {GL}}_n(K))$
. Note that, for any group G, by
$\operatorname {\mathrm {GL}}_n(K) / Z(\operatorname {\mathrm {GL}}_n(K))$
. Note that, for any group G, by
![]() $Z(G),$
we denote the center of the group. We define
$Z(G),$
we denote the center of the group. We define
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
to be any nontrivial semidirect product of
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
to be any nontrivial semidirect product of
![]() $Q_8$
by a cyclic 3-group.
$Q_8$
by a cyclic 3-group.
For a finite group G, we denote the set of all irreducible characters of G by Irr
![]() $(G)$
. If H is a subgroup of G and
$(G)$
. If H is a subgroup of G and
![]() $\chi $
is a character of G, then
$\chi $
is a character of G, then
![]() $\chi |_H$
denotes the restriction of
$\chi |_H$
denotes the restriction of
![]() $\chi $
to H. Whereas, if
$\chi $
to H. Whereas, if
![]() $\psi $
is a character of H, by Ind
$\psi $
is a character of H, by Ind
![]() $_H^G \psi $
, we denote the induced character defined as
$_H^G \psi $
, we denote the induced character defined as
We denote the usual inner product on the space of complex class functions on G by
![]() $\langle \_, \_ \rangle $
. It is given by
$\langle \_, \_ \rangle $
. It is given by
 $$ \begin{align*}\langle \alpha, \beta \rangle = \frac{1}{|G|} \sum_{g \in G} \alpha(g) \overline{\beta(g)}.\end{align*} $$
$$ \begin{align*}\langle \alpha, \beta \rangle = \frac{1}{|G|} \sum_{g \in G} \alpha(g) \overline{\beta(g)}.\end{align*} $$
Frobenius reciprocity theorem tells us that for any
![]() $\chi $
and
$\chi $
and
![]() $\psi $
as above, we have
$\psi $
as above, we have
![]() $\langle \text {Ind}_H^G \psi , \chi \rangle = \langle \psi , \chi |_H \rangle _H$
, where
$\langle \text {Ind}_H^G \psi , \chi \rangle = \langle \psi , \chi |_H \rangle _H$
, where
![]() $\langle \_, \_ \rangle _H$
is the usual inner product on the space of complex class functions on the subgroup H. We denote the regular character of G by “reg.” Note that
$\langle \_, \_ \rangle _H$
is the usual inner product on the space of complex class functions on the subgroup H. We denote the regular character of G by “reg.” Note that
In general, by a virtual character of G, we mean a class function
![]() $\sum _{\chi \in \text {Irr}(G)} a_{\chi } \chi $
, where
$\sum _{\chi \in \text {Irr}(G)} a_{\chi } \chi $
, where
![]() $a_{\chi } \in \mathbb {Z}$
. In particular,
$a_{\chi } \in \mathbb {Z}$
. In particular,
![]() $a_{\chi }$
can be negative.
$a_{\chi }$
can be negative.
We have written
![]() $E/K$
to denote an elliptic curve E defined over the field K. We denote the L-series of E over K by
$E/K$
to denote an elliptic curve E defined over the field K. We denote the L-series of E over K by
![]() $L(E/K,s)$
. If
$L(E/K,s)$
. If
![]() $F/K$
is a Galois extension and
$F/K$
is a Galois extension and
![]() $\chi $
is a character of
$\chi $
is a character of
![]() ${\text {Gal}}(F/K),$
then the twisted L-series of E over K by
${\text {Gal}}(F/K),$
then the twisted L-series of E over K by
![]() $\chi $
is denoted by
$\chi $
is denoted by
![]() $L(E/K \otimes \chi , s)$
, whereas,
$L(E/K \otimes \chi , s)$
, whereas,
![]() $L(s,\chi )$
has been used to denote the Artin L-function corresponding to
$L(s,\chi )$
has been used to denote the Artin L-function corresponding to
![]() $\chi $
of
$\chi $
of
![]() ${\text {Gal}}(F/K)$
.
${\text {Gal}}(F/K)$
.
2 Algebraic minimal subfield
Definition 2.1 Let
![]() $E/K$
be an elliptic curve, and let
$E/K$
be an elliptic curve, and let
![]() $L/K$
be a finite extension (not necessarily Galois) of number fields. Suppose that
$L/K$
be a finite extension (not necessarily Galois) of number fields. Suppose that
![]() ${\mathbf {rk}} E(L) = r$
. The algebraic minimal subfield M is a subfield with
${\mathbf {rk}} E(L) = r$
. The algebraic minimal subfield M is a subfield with
![]() $K \subseteq M \subseteq L$
satisfying:
$K \subseteq M \subseteq L$
satisfying:
-
(i)
 ${\mathbf {rk}} E(M) = r$
, and
${\mathbf {rk}} E(M) = r$
, and -
(ii) if
 $K \subseteq F \subseteq L$
with
$K \subseteq F \subseteq L$
with
 ${\mathbf {rk}} E(F) = r $
, then
${\mathbf {rk}} E(F) = r $
, then
 $M \subseteq F$
.
$M \subseteq F$
.
Akbary and Murty showed that for any finite extension
![]() $L/K$
and elliptic curve
$L/K$
and elliptic curve
![]() $E/ K$
, the minimal subfield M exists and is unique. Also, if
$E/ K$
, the minimal subfield M exists and is unique. Also, if
![]() $L/K$
is Galois, then
$L/K$
is Galois, then
![]() $M/K$
is Galois (see [Reference Akbary and Kumar Murty1, Proposition 1]). For any finite Galois extension
$M/K$
is Galois (see [Reference Akbary and Kumar Murty1, Proposition 1]). For any finite Galois extension
![]() $L/K$
, the Galois group
$L/K$
, the Galois group
![]() ${\text {Gal}}(L/K)$
acts on
${\text {Gal}}(L/K)$
acts on
![]() $E(L) \otimes {\mathbb Q}$
giving us a representation (writing
$E(L) \otimes {\mathbb Q}$
giving us a representation (writing
![]() $r = {\mathbf {rk}} E(L)$
)
$r = {\mathbf {rk}} E(L)$
)
Proposition 2.1 Let
![]() $L/K$
be a finite Galois extension with
$L/K$
be a finite Galois extension with
![]() ${\mathbf {rk}} E(L) = r$
, and let M be the minimal subfield. Then
${\mathbf {rk}} E(L) = r$
, and let M be the minimal subfield. Then
is faithful. Moreover, Im
![]() $(\rho )$
is conjugate to a finite subgroup of
$(\rho )$
is conjugate to a finite subgroup of
![]() $\operatorname {\mathrm {GL}}_r({\mathbb Z}).$
$\operatorname {\mathrm {GL}}_r({\mathbb Z}).$
For a detailed proof, see [Reference Akbary and Kumar Murty1, Proposition 2]. But the essential idea is that M is constructed as the fixed field of
![]() $\ker \rho _L$
.
$\ker \rho _L$
.
2.1 Working with the quotient space
We will write
![]() $V_F = E(F) \otimes {\mathbb Q}$
for any number field F. We will work with the quotient space
$V_F = E(F) \otimes {\mathbb Q}$
for any number field F. We will work with the quotient space
![]() $V_L / V_K $
instead of
$V_L / V_K $
instead of
![]() $V_L$
and use elementary linear algebra to prove a similar version of the above proposition. Note that dimension of this quotient space is precisely the increase in rank, i.e.,
$V_L$
and use elementary linear algebra to prove a similar version of the above proposition. Note that dimension of this quotient space is precisely the increase in rank, i.e.,
We can then consider the quotient representation coming from the Galois action. For the algebraic minimal subfield, this representation also turns out to be faithful.
Proposition 2.2 Let
![]() $L/K$
be a finite Galois extension with
$L/K$
be a finite Galois extension with
![]() ${\mathbf {rk}} E(L) = r$
, and let M be the algebraic minimal subfield. If
${\mathbf {rk}} E(L) = r$
, and let M be the algebraic minimal subfield. If
![]() $ {\mathbf {rk}} E(L) - {\mathbf {rk}} E(K) = t$
, then there exists a faithful representation
$ {\mathbf {rk}} E(L) - {\mathbf {rk}} E(K) = t$
, then there exists a faithful representation
Moreover, Im
![]() $(\tilde {\rho })$
is conjugate to a finite subgroup of
$(\tilde {\rho })$
is conjugate to a finite subgroup of
![]() $\operatorname {\mathrm {GL}}_t({\mathbb Z})$
.
$\operatorname {\mathrm {GL}}_t({\mathbb Z})$
.
Proof By Proposition 2.1, we know there is a faithful representation
![]() $\rho : {\text {Gal}}(M / K) \kern1.2pt{\rightarrow} \operatorname {\mathrm {GL}}(V_{M})$
. We can then consider the quotient representation
$\rho : {\text {Gal}}(M / K) \kern1.2pt{\rightarrow} \operatorname {\mathrm {GL}}(V_{M})$
. We can then consider the quotient representation
![]() $\tilde {\rho } : {\text {Gal}}(M / K) \rightarrow \operatorname {\mathrm {GL}}(V_{M}/V_K)$
, where
$\tilde {\rho } : {\text {Gal}}(M / K) \rightarrow \operatorname {\mathrm {GL}}(V_{M}/V_K)$
, where
![]() $\tilde {\rho }(g) \cdot \left (v + V_K\right ) = \rho (g)\cdot v + V_K$
.
$\tilde {\rho }(g) \cdot \left (v + V_K\right ) = \rho (g)\cdot v + V_K$
.
Now, let us compute
![]() $\ker \tilde {\rho }$
:
$\ker \tilde {\rho }$
:
 $$ \begin{align*} & \tilde{\rho}(g) (v + V_K) = \tilde{\rho}(1) (v + V_K) \\ &\Rightarrow \rho(g) v - v \in V_K \\ & \Rightarrow \rho(g) \left(\rho(g) v - v \right)= \rho(g)v - v \;\;\;\;\; \text{[Since } g \text{ acts trivially on } V_K]\\ & \Rightarrow (\rho(g)^2 - 2 \rho(g) + I_t)v = 0 \;\;\; \text{ for all } v \in V_{M}. \end{align*} $$
$$ \begin{align*} & \tilde{\rho}(g) (v + V_K) = \tilde{\rho}(1) (v + V_K) \\ &\Rightarrow \rho(g) v - v \in V_K \\ & \Rightarrow \rho(g) \left(\rho(g) v - v \right)= \rho(g)v - v \;\;\;\;\; \text{[Since } g \text{ acts trivially on } V_K]\\ & \Rightarrow (\rho(g)^2 - 2 \rho(g) + I_t)v = 0 \;\;\; \text{ for all } v \in V_{M}. \end{align*} $$
Thus, the minimal polynomial of
![]() $\rho (g)$
divides the polynomial
$\rho (g)$
divides the polynomial
![]() $x^2 - 2x + 1 = (x-1)^2$
. Since
$x^2 - 2x + 1 = (x-1)^2$
. Since
![]() ${\text {Gal}}(M/K)$
is finite, the minimal polynomial will also divide
${\text {Gal}}(M/K)$
is finite, the minimal polynomial will also divide
![]() $x^n - 1$
, where
$x^n - 1$
, where
![]() ${n = |{\text {Gal}}(M/K)|}$
. Thus, the minimal polynomial must be
${n = |{\text {Gal}}(M/K)|}$
. Thus, the minimal polynomial must be
![]() $x-1$
, and hence we have
$x-1$
, and hence we have
![]() $\rho (g) = I_t = \rho (1)$
. Since
$\rho (g) = I_t = \rho (1)$
. Since
![]() $\rho $
is faithful, this implies
$\rho $
is faithful, this implies
![]() $g=1$
. Thus
$g=1$
. Thus
![]() $\tilde {\rho }$
is also faithful.
$\tilde {\rho }$
is also faithful.
The fixed assertion is true more generally, any finite subgroup of
![]() $\operatorname {\mathrm {GL}}_n({\mathbb Q})$
has a conjugate in
$\operatorname {\mathrm {GL}}_n({\mathbb Q})$
has a conjugate in
![]() $\operatorname {\mathrm {GL}}_n({\mathbb Z})$
. For a proof, see [Reference Serre23, Theorem 1 and Appendix 3, p. 124].
$\operatorname {\mathrm {GL}}_n({\mathbb Z})$
. For a proof, see [Reference Serre23, Theorem 1 and Appendix 3, p. 124].
In the next subsection, we present a number of elementary results from group theory as lemmas. These together with Proposition 2.2 will help us to prove Theorem 1.1.
2.2 Results from group theory
Lemma 2.3 Let
![]() $\rho : G \rightarrow \operatorname {\mathrm {GL}}_2({\mathbb Z})$
be a faithful representation.
$\rho : G \rightarrow \operatorname {\mathrm {GL}}_2({\mathbb Z})$
be a faithful representation.
-
(1) If
 $\rho $
is reducible, then
$\rho $
is reducible, then
 $G \cong C_n$
or,
$G \cong C_n$
or,
 $\; {\mathbb Z}/2{\mathbb Z} \oplus {\mathbb Z}/2{\mathbb Z}$
, where
$\; {\mathbb Z}/2{\mathbb Z} \oplus {\mathbb Z}/2{\mathbb Z}$
, where
 $n=1,2,3,4,6$
.
$n=1,2,3,4,6$
. -
(2) If
 $\rho $
is irreducible, then
$\rho $
is irreducible, then
 $G \cong D_{2n}$
, where
$G \cong D_{2n}$
, where
 $n=3,4,6$
.
$n=3,4,6$
.
Lemma 2.4 Let
![]() $\rho : G \rightarrow \operatorname {\mathrm {GL}}_3({\mathbb Z})$
be a faithful representation. Then G is isomorphic to one of the following:
$\rho : G \rightarrow \operatorname {\mathrm {GL}}_3({\mathbb Z})$
be a faithful representation. Then G is isomorphic to one of the following:
-
 $C_n \times C_m, $
where
$C_n \times C_m, $
where
 $ n=1,2,3,4 $
and
$ n=1,2,3,4 $
and
 $ m=1,2,$
$ m=1,2,$
-
 $D_{2p} \times C_m,$
where
$D_{2p} \times C_m,$
where
 $ p=2, 3, 4, 6 $
and
$ p=2, 3, 4, 6 $
and
 $ m=1,2,$
$ m=1,2,$
-
 $ A_4 \times C_m,$
where
$ A_4 \times C_m,$
where
 $m=1,2,$
or
$m=1,2,$
or -
 $S_4 \times C_m, $
where
$S_4 \times C_m, $
where
 $m=1,2$
.
$m=1,2$
.
For proofs, see [Reference Akbary and Kumar Murty1, Section 3].
2.3 Proof of Theorem 1.1
Proof For the
![]() $t=1$
case, by Proposition 2.2, the Galois group
$t=1$
case, by Proposition 2.2, the Galois group
![]() ${\text {Gal}}(M/K)$
is isomorphic to a subgroup of
${\text {Gal}}(M/K)$
is isomorphic to a subgroup of
![]() $\operatorname {\mathrm {GL}}_1({\mathbb Z}) = \{ \pm 1 \}$
. Since the rank has increased,
$\operatorname {\mathrm {GL}}_1({\mathbb Z}) = \{ \pm 1 \}$
. Since the rank has increased,
![]() $M \neq K$
, so we must have
$M \neq K$
, so we must have
![]() $[M:K] = 2$
. Applying Proposition 2.2 and the above Lemmas 2.3 and 2.4, we directly get the
$[M:K] = 2$
. Applying Proposition 2.2 and the above Lemmas 2.3 and 2.4, we directly get the
![]() $t=2$
and
$t=2$
and
![]() $t=3$
case.
$t=3$
case.
Theorem 1.1(1) is particularly interesting as it implies the following.
Corollary 2.5 In any extension of odd degree, particularly in a cubic extension, the rank can not increase by
![]() $1$
. It either remains the same or jumps by at least
$1$
. It either remains the same or jumps by at least
![]() $2$
.
$2$
.
Remark 2.6 Note that generalization to larger values of t becomes heavily reliant on the knowledge of classification of finite subgroups of
![]() $\operatorname {\mathrm {GL}}_n({\mathbb Z})$
. However, we present here the following easily observed result. We haven’t included it as a theorem as the author is unsure of whether or not it is vacuous.
$\operatorname {\mathrm {GL}}_n({\mathbb Z})$
. However, we present here the following easily observed result. We haven’t included it as a theorem as the author is unsure of whether or not it is vacuous.
Let
![]() $L/K$
be a solvable Galois extension of degree n such that
$L/K$
be a solvable Galois extension of degree n such that
![]() ${\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
, where t is odd. Let M be its minimal subfield. If the quotient representation
${\mathbf {rk}} E(L) = {\mathbf {rk}} E(K) + t$
, where t is odd. Let M be its minimal subfield. If the quotient representation
![]() $\tilde {\rho } : {\text {Gal}}(M /K) \rightarrow \operatorname {\mathrm {GL}}_t({\mathbb Q})$
is irreducible, then
$\tilde {\rho } : {\text {Gal}}(M /K) \rightarrow \operatorname {\mathrm {GL}}_t({\mathbb Q})$
is irreducible, then
![]() $t \; | \; n$
. The proof follows from the two results stated below.
$t \; | \; n$
. The proof follows from the two results stated below.
-
(a) Let G be a finite group. The degree of every irreducible representation of G over an algebraically closed field
 $\mathbf {k}$
of characteristic 0, divides the order of G.
$\mathbf {k}$
of characteristic 0, divides the order of G.For a proof, see [Reference Serre25, Section 6.5].
-
(b) Theorem (Dixon) Let G be a finite solvable irreducible subgroup of
 $\operatorname {\mathrm {GL}}_n( K),$
where K is a real field and n is an odd integer. Then G is absolutely irreducible.
$\operatorname {\mathrm {GL}}_n( K),$
where K is a real field and n is an odd integer. Then G is absolutely irreducible.For a proof, see [Reference Dixon6, Theorem 1] and [Reference Dixon7].
Note that by absolutely irreducible, we mean that G is irreducible over the algebraic closure
![]() $\overline {K}$
of K. If in fact,
$\overline {K}$
of K. If in fact,
![]() $t=p$
is prime, then the above mentioned papers of Dixon will provide a nice description of the Galois Group. But we think that requiring
$t=p$
is prime, then the above mentioned papers of Dixon will provide a nice description of the Galois Group. But we think that requiring
![]() $\tilde {\rho }$
to be irreducible for larger ranks, might be asking too much!
$\tilde {\rho }$
to be irreducible for larger ranks, might be asking too much!
3 Analytic minimal subfield
In this section, we focus on the analytic counterpart of the algebraic minimal subfield.
Definition 3.1 Let
![]() $E/K$
be an elliptic curve, and let F be any finite extension of K. For each zero
$E/K$
be an elliptic curve, and let F be any finite extension of K. For each zero
![]() $\omega $
of
$\omega $
of
![]() $L(E/F,s)$
, the analytic minimal subfield
$L(E/F,s)$
, the analytic minimal subfield
![]() $F_{\omega }$
is a subfield of F with
$F_{\omega }$
is a subfield of F with
![]() $K \subseteq F_{\omega } \subseteq F$
such that:
$K \subseteq F_{\omega } \subseteq F$
such that:
(i) ord
![]() $_{s=\omega } \; L(E/F_{\omega },s) =$
ord
$_{s=\omega } \; L(E/F_{\omega },s) =$
ord
![]() $_{s= \omega } \;L(E/F, s)$
, and
$_{s= \omega } \;L(E/F, s)$
, and
(ii) if
![]() $K \subseteq M \subseteq F$
and ord
$K \subseteq M \subseteq F$
and ord
![]() $_{s=\omega } \; L(E/M,s) =$
ord
$_{s=\omega } \; L(E/M,s) =$
ord
![]() $_{s= \omega } \;L(E/F, s)$
, then
$_{s= \omega } \;L(E/F, s)$
, then
![]() $F_{\omega } \subseteq M$
.
$F_{\omega } \subseteq M$
.
Proposition 3.1 If
![]() $F/K$
is Galois with Galois group G and
$F/K$
is Galois with Galois group G and
![]() $L(E/K \otimes \chi , s)$
is holomorphic at
$L(E/K \otimes \chi , s)$
is holomorphic at
![]() $s=\omega $
for any irreducible character
$s=\omega $
for any irreducible character
![]() $\chi $
of G, then
$\chi $
of G, then
![]() $F_{\omega } $
exists and is Galois over K.
$F_{\omega } $
exists and is Galois over K.
For a detailed proof, see [Reference Akbary and Kumar Murty1, Proposition 6]. We briefly mention the construction here, as we will be using this in Section 6. The idea is to consider those characters for which the twisted L-function vanishes at
![]() $\omega $
, i.e.,
$\omega $
, i.e.,
Then define
The minimal subfield
![]() $F_\omega $
is then the fixed field,
$F_\omega $
is then the fixed field,
![]() $K^{H_{\omega }}$
of
$K^{H_{\omega }}$
of
![]() $H_{\omega }$
in F.
$H_{\omega }$
in F.
Therefore from Proposition 3.1, in order to work with
![]() $F_{\omega }$
, we first need to investigate holomorphy of
$F_{\omega }$
, we first need to investigate holomorphy of
![]() $L(E/K \otimes \chi , s)$
at
$L(E/K \otimes \chi , s)$
at
![]() $s= \omega $
. We recall some classical theorems on Artin’s holomorphy conjecture. Let
$s= \omega $
. We recall some classical theorems on Artin’s holomorphy conjecture. Let
![]() $F/K$
be a Galois extension.
$F/K$
be a Galois extension.
Theorem 3.2
(Stark) If
![]() $s_0$
is a simple zero of the Dedekind zeta function
$s_0$
is a simple zero of the Dedekind zeta function
![]() $\zeta _{F}(s)$
, then
$\zeta _{F}(s)$
, then
![]() $L(s,\chi )$
is analytic at
$L(s,\chi )$
is analytic at
![]() $s=s_0$
for every irreducible character
$s=s_0$
for every irreducible character
![]() $\chi $
of
$\chi $
of
![]() $\mathrm{Gal}(F/K)$
.
$\mathrm{Gal}(F/K)$
.
For a proof, see [Reference Stark26, Theorem 3, p. 144].
Definition 3.2 We say E satisfies the generalized Taniyama conjecture over a number field K if the L-function
![]() $L(E/K, s)$
is the L-function
$L(E/K, s)$
is the L-function
![]() $L(\pi , s)$
of a cuspidal automorphic representation
$L(\pi , s)$
of a cuspidal automorphic representation
![]() $\pi $
of
$\pi $
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_K )$
, where
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_K )$
, where
![]() $\mathbb {A}_K$
is the adèle ring of K.
$\mathbb {A}_K$
is the adèle ring of K.
Note that for
![]() $K={\mathbb Q}$
, the above conjecture is known and is called The Modularity Theorem. The name derives from the fact that if
$K={\mathbb Q}$
, the above conjecture is known and is called The Modularity Theorem. The name derives from the fact that if
![]() $E/{\mathbb Q}$
is an elliptic curve, then its L-function
$E/{\mathbb Q}$
is an elliptic curve, then its L-function
![]() $L(E/{\mathbb Q},s)$
is the L-function of a modular form. In 1995, Wiles and Taylor first proved the conjecture for semi-stable elliptic curves defined over
$L(E/{\mathbb Q},s)$
is the L-function of a modular form. In 1995, Wiles and Taylor first proved the conjecture for semi-stable elliptic curves defined over
![]() ${\mathbb Q}$
and in 2001, B. Conrad, F. Diamond, Richard Taylor, and C. Breuil, proved modularity for all elliptic curves defined over
${\mathbb Q}$
and in 2001, B. Conrad, F. Diamond, Richard Taylor, and C. Breuil, proved modularity for all elliptic curves defined over
![]() $\mathbb {Q}$
. From works of Taylor, Kisin, Wintenberger, and others, the following result on “potential modularity” is also known: If
$\mathbb {Q}$
. From works of Taylor, Kisin, Wintenberger, and others, the following result on “potential modularity” is also known: If
![]() $E/K$
is an elliptic curve, where K is a totally real field, then there is a totally real extension
$E/K$
is an elliptic curve, where K is a totally real field, then there is a totally real extension
![]() $L/K$
such that
$L/K$
such that
![]() $E/L$
is modular (see, for example, [Reference Breuil, Conrad, Diamond and Taylor3, Reference Kisin16, Reference Taylor and Wiles27, Reference Wiles29]).
$E/L$
is modular (see, for example, [Reference Breuil, Conrad, Diamond and Taylor3, Reference Kisin16, Reference Taylor and Wiles27, Reference Wiles29]).
The following elliptic analogue of Stark’s theorem is due to Akbary and Murty (see [Reference Akbary and Kumar Murty1, Proposition 7]).
Theorem 3.3
(Akbary–Murty) Let
![]() $E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a solvable extension of K, and let
$E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a solvable extension of K, and let
![]() $\chi $
be an irreducible character of
$\chi $
be an irreducible character of
![]() $G =\mathrm{Gal}(F/K)$
. Then,
$G =\mathrm{Gal}(F/K)$
. Then,
![]() $L(E/K \otimes \chi , s)$
is holomorphic at
$L(E/K \otimes \chi , s)$
is holomorphic at
![]() $s = \omega $
, if
$s = \omega $
, if
![]() $\omega $
is a simple zero of
$\omega $
is a simple zero of
![]() $L(E/F, s)$
.
$L(E/F, s)$
.
Using this, they showed, under the same assumptions of the theorem, the analytic minimal subfield
![]() $F_{\omega }$
exists. Moreover,
$F_{\omega }$
exists. Moreover,
![]() $F_{\omega }$
is a cyclic extension of K and if
$F_{\omega }$
is a cyclic extension of K and if
![]() $\omega $
is real, then
$\omega $
is real, then
![]() $[F_{\omega } :K]\leq 2$
. Regarding Artin’s holomorphy conjecture, some generalizations of Theorem 3.2 of Stark, are known. These results, as stated below, are due to Foote, Murty, and Wales. They ease the condition on
$[F_{\omega } :K]\leq 2$
. Regarding Artin’s holomorphy conjecture, some generalizations of Theorem 3.2 of Stark, are known. These results, as stated below, are due to Foote, Murty, and Wales. They ease the condition on
![]() $\omega $
, from being a simple zero to a zero of small order. In the next section, we will prove the elliptic analogue of such theorems.
$\omega $
, from being a simple zero to a zero of small order. In the next section, we will prove the elliptic analogue of such theorems.
Theorem 3.4
(Foote–Wales) Let
![]() $F/K$
be a Galois extension of number fields with solvable Galois group G. If the Dedekind zeta function of F,
$F/K$
be a Galois extension of number fields with solvable Galois group G. If the Dedekind zeta function of F,
![]() $\zeta _F(s)$
, has a zero at
$\zeta _F(s)$
, has a zero at
![]() $s=s_0$
of order less than or equal to
$s=s_0$
of order less than or equal to
![]() $2$
, then all Artin L-series
$2$
, then all Artin L-series
![]() $L(s, \chi )$
are analytic at
$L(s, \chi )$
are analytic at
![]() $s=s_0$
for every irreducible character
$s=s_0$
for every irreducible character
![]() $\chi $
of G.
$\chi $
of G.
For a proof, see the corollary of [Reference Foote and Wales10, Theorem II].
Theorem 3.5
(Foote–Murty) Let
![]() $F/K$
be a Galois extension of number fields with solvable Galois group G, and let
$F/K$
be a Galois extension of number fields with solvable Galois group G, and let
![]() $p_2$
be the second smallest prime number dividing
$p_2$
be the second smallest prime number dividing
![]() $|G|$
. If
$|G|$
. If
![]() $\zeta _F(s)$
has a zero of order r at
$\zeta _F(s)$
has a zero of order r at
![]() $s=s_0$
, where
$s=s_0$
, where
![]() $r \leq p_2-2$
, then
$r \leq p_2-2$
, then
![]() $L(s,\chi )$
is analytic at
$L(s,\chi )$
is analytic at
![]() $s_0$
for all irreducible characters
$s_0$
for all irreducible characters
![]() $\chi $
of G.
$\chi $
of G.
For a proof, see [Reference Foote and Kumar Murty9, p. Reference Feit8]. Also note that, in case
![]() $|G|$
has only one prime factor, i.e.,
$|G|$
has only one prime factor, i.e.,
![]() $|G|$
is a prime power, then G is nilpotent and
$|G|$
is a prime power, then G is nilpotent and
![]() $L(s,\chi )$
is known to be analytic in such cases. The key idea behind both of the above two results, was an attempt in finding minimal counterexamples to Artin’s holomorphy conjecture.
$L(s,\chi )$
is known to be analytic in such cases. The key idea behind both of the above two results, was an attempt in finding minimal counterexamples to Artin’s holomorphy conjecture.
3.1 Automorphic representations and nilpotent Galois groups
Assuming the generalized Taniyama Conjecture for K, M. Ram Murty and V. Kumar Murty in [Reference Murty and Kumar Murty21] proved that if
![]() $F/K$
is contained in a finite solvable Galois extension of K, then
$F/K$
is contained in a finite solvable Galois extension of K, then
![]() $L(E/F,s)$
is holomorphic. Their result is predicted by a more general conjecture in Langlands program which states that if
$L(E/F,s)$
is holomorphic. Their result is predicted by a more general conjecture in Langlands program which states that if
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
are cuspidal automorphic representations of
$\pi _2$
are cuspidal automorphic representations of
![]() $\operatorname {\mathrm {GL}}_n(\mathbb {A}_K)$
and
$\operatorname {\mathrm {GL}}_n(\mathbb {A}_K)$
and
![]() $\operatorname {\mathrm {GL}}_m(\mathbb {A}_K)$
, respectively, then
$\operatorname {\mathrm {GL}}_m(\mathbb {A}_K)$
, respectively, then
![]() $\pi _1 \otimes \pi _2$
is an automorphic representation of
$\pi _1 \otimes \pi _2$
is an automorphic representation of
![]() $\operatorname {\mathrm {GL}}_{nm}(\mathbb {A}_K)$
. This is known for
$\operatorname {\mathrm {GL}}_{nm}(\mathbb {A}_K)$
. This is known for
![]() $m=1$
, as abelian twists are automorphic. The
$m=1$
, as abelian twists are automorphic. The
![]() $\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(2)$
case was proved by Ramakrishnan in [Reference Ramakrishnan22] and the
$\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(2)$
case was proved by Ramakrishnan in [Reference Ramakrishnan22] and the
![]() $\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(3)$
by Kim and Shahidi in [Reference Kim and Shahidi15]. In [Reference Arthur and Clozel2], Arthur and Clozel proved that the Langlands reciprocity is valid for all nilpotent Galois extensions using their theory of automorphic induction. Therefore, assuming the generalized Taniyama conjecture for
$\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(3)$
by Kim and Shahidi in [Reference Kim and Shahidi15]. In [Reference Arthur and Clozel2], Arthur and Clozel proved that the Langlands reciprocity is valid for all nilpotent Galois extensions using their theory of automorphic induction. Therefore, assuming the generalized Taniyama conjecture for
![]() $E/K$
, and for an extension
$E/K$
, and for an extension
![]() $F/K$
with nilpotent Gal
$F/K$
with nilpotent Gal
![]() $(F/K)$
, we see that
$(F/K)$
, we see that
![]() $L (E/K \otimes \chi , s)$
is automorphic for any irreducible character
$L (E/K \otimes \chi , s)$
is automorphic for any irreducible character
![]() $\chi $
of Gal
$\chi $
of Gal
![]() $(F/K)$
.
$(F/K)$
.
Recently Wong [Reference Wong30] have generalized the above result to certain cases of “nearly nilpotent” and “abelian-by-nilpotent” Galois extensions. In a subsequent section, while proving the elliptic analogue of Foote–Wales’s theorem, we will use similar ideas to eliminate one of the possibilities.
4 Elliptic analogue of Foote and Murty’s Theorem
Theorem 4.1 Let
![]() $E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
$E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
![]() $G=$
$G=$
![]() $\mathrm{Gal}(F/K)$
. Let
$\mathrm{Gal}(F/K)$
. Let
![]() $\chi $
be an irreducible character of G. Then,
$\chi $
be an irreducible character of G. Then,
![]() $L(E/K \otimes \chi , s)$
is holomorphic at
$L(E/K \otimes \chi , s)$
is holomorphic at
![]() $s = \omega $
if
$s = \omega $
if
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F, s)$
of order
$L(E/F, s)$
of order
![]() $r \leq p_2 - 2$
, where
$r \leq p_2 - 2$
, where
![]() $p_2$
is the second smallest prime factor of
$p_2$
is the second smallest prime factor of
![]() $|G|$
.
$|G|$
.
Remark 4.2 Note that if
![]() $|G|$
has only one prime factor, then G is nilpotent. Hence from the above discussion,
$|G|$
has only one prime factor, then G is nilpotent. Hence from the above discussion,
![]() $L(E/K \otimes \chi , s)$
is known to be automorphic.
$L(E/K \otimes \chi , s)$
is known to be automorphic.
As an immediate corollary we get the following.
Corollary 4.3 Under the same conditions of the above theorem, the minimal subfield
![]() $F_{\omega }$
exists if
$F_{\omega }$
exists if
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F, s)$
of order
$L(E/F, s)$
of order
![]() $r \leq p_2 - 2$
, where
$r \leq p_2 - 2$
, where
![]() $p_2$
is the second smallest prime factor of
$p_2$
is the second smallest prime factor of
![]() $|G|$
.
$|G|$
.
4.1 Ingredients for the proof of Theorem 4.1
The following Aramata–Brauer-type theorem was proved in [Reference Murty and Kumar Murty21, Theorem 2].
Theorem 4.4 Let
![]() $E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. If F is a solvable Galois extension of K, then
$E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. If F is a solvable Galois extension of K, then
![]() $L(E/F,s)$
extends to an entire function and
$L(E/F,s)$
extends to an entire function and
![]() $ {L(E/F,s)}/{ L(E/K,s)} $
is entire. In particular,
$ {L(E/F,s)}/{ L(E/K,s)} $
is entire. In particular,
We now list some results on finite groups and virtual Heilbronn characters that will be used to prove Theorem 4.1.
Let
![]() $F/K$
be a finite Galois extension with Galois group G. Let H be a subgroup of G. Let
$F/K$
be a finite Galois extension with Galois group G. Let H be a subgroup of G. Let
![]() $\chi $
and
$\chi $
and
![]() $\psi $
denote the irreducible characters of G and H, respectively. Consider the virtual Heilbronn characters
$\psi $
denote the irreducible characters of G and H, respectively. Consider the virtual Heilbronn characters
where
![]() $n_{\chi }$
denotes the order of zero of
$n_{\chi }$
denotes the order of zero of
![]() $L(E/K\otimes \chi , s)$
at
$L(E/K\otimes \chi , s)$
at
![]() $s=\omega $
and
$s=\omega $
and
![]() $n_{\psi }$
denotes the order of zero of
$n_{\psi }$
denotes the order of zero of
![]() $L(E/F^H \otimes \psi , s)$
at
$L(E/F^H \otimes \psi , s)$
at
![]() $s = \omega $
(
$s = \omega $
(
![]() $F^H$
being the fixed field of H).
$F^H$
being the fixed field of H).
Proposition 4.5
![]() $\theta _{G} |_{H} = \theta _{H}$
.
$\theta _{G} |_{H} = \theta _{H}$
.
For a proof, see [Reference Murty and Kumar Murty21, Proposition 1].
Theorem 4.6 (Blichfeldt)
Let G be a finite group admitting a faithful, irreducible complex representation
![]() $\rho $
. If G possesses a noncentral abelian normal subgroup, then
$\rho $
. If G possesses a noncentral abelian normal subgroup, then
![]() $\rho $
is induced from a proper subgroup of G.
$\rho $
is induced from a proper subgroup of G.
For a proof, see [Reference Curtis and Reiner5, Corollary 50.7, p. 348].
Theorem 4.7
(Ito) Let G be a solvable group, and let p be a prime such that G has a faithful character of degree
![]() $< p-1$
. Then G admits an abelian normal Sylow p-subgroup.
$< p-1$
. Then G admits an abelian normal Sylow p-subgroup.
For a proof, see [Reference Feit8, Theorem 24.6, p. 128].
Proposition 4.8 Any solvable non-abelian group G has a normal subgroup N of prime index such that N contains
![]() $Z(G)$
.
$Z(G)$
.
Proof Since G is non-abelian,
![]() $G_1 = G/Z(G)$
is a nontrivial solvable group. Let H be a maximal normal subgroup of
$G_1 = G/Z(G)$
is a nontrivial solvable group. Let H be a maximal normal subgroup of
![]() $G_1$
. Then
$G_1$
. Then
![]() $G_1/H$
is solvable and simple and hence is cyclic of prime order. Thus, the index of H in
$G_1/H$
is solvable and simple and hence is cyclic of prime order. Thus, the index of H in
![]() $G_1$
is prime. Taking N to be the pre-image of
$G_1$
is prime. Taking N to be the pre-image of
![]() $H_1$
proves the proposition.
$H_1$
proves the proposition.
We also recall the following result from Clifford’s theory (see [Reference Feit8, pp. 53–54]).
Proposition 4.9 Let N be a normal subgroup of G with
![]() $[G : N] = p$
, a prime. Then for any irreducible character
$[G : N] = p$
, a prime. Then for any irreducible character
![]() $\chi $
of G, either
$\chi $
of G, either
![]() $\chi |_N$
is irreducible, or
$\chi |_N$
is irreducible, or
![]() $\chi |_N = \sum _{i=1}^p \psi _i$
, where
$\chi |_N = \sum _{i=1}^p \psi _i$
, where
![]() $\psi _i$
are distinct and irreducible characters of N. Moreover,
$\psi _i$
are distinct and irreducible characters of N. Moreover,
![]() $\chi = $
Ind
$\chi = $
Ind
![]() $_H^G \psi _i$
.
$_H^G \psi _i$
.
4.2 Proof of Theorem 4.1
The proof is based on the idea of minimal counterexamples as that of its classical counterpart. Assume the theorem is false and suppose F and K are chosen to form a counterexample with
![]() $[F:K]$
minimal. Thus there exists an irreducible character
$[F:K]$
minimal. Thus there exists an irreducible character
![]() $\chi $
of G and a point
$\chi $
of G and a point
![]() $s= \omega $
such that
$s= \omega $
such that
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F,s)$
of order satisfying the conditions in the theorem but
$L(E/F,s)$
of order satisfying the conditions in the theorem but
![]() $L(E/K \otimes \chi , s)$
has a pole at
$L(E/K \otimes \chi , s)$
has a pole at
![]() $s=\omega $
, i.e.,
$s=\omega $
, i.e.,
![]() $n_{\chi }<0$
in the virtual Heilbronn character
$n_{\chi }<0$
in the virtual Heilbronn character
![]() $\theta _G$
at
$\theta _G$
at
![]() $s=\omega $
.
$s=\omega $
.
Note that G can not be cyclic, since
![]() $L(E/K \otimes \chi , s)$
is known to be analytic for cyclic extensions
$L(E/K \otimes \chi , s)$
is known to be analytic for cyclic extensions
![]() $F/K$
for every irreducible character
$F/K$
for every irreducible character
![]() $\chi $
of G (see, for example, the proof of [Reference Murty and Kumar Murty21, Theorem 2, p. 492]).
$\chi $
of G (see, for example, the proof of [Reference Murty and Kumar Murty21, Theorem 2, p. 492]).
-
Step 1 : Every irreducible character
 $\chi $
of G with
$\chi $
of G with
 $n_{\chi } < 0$
is faithful.
$n_{\chi } < 0$
is faithful.Note that by Theorem 4.4, for every field D with
 $K \subseteq D \subseteq F$
, we have ord
$K \subseteq D \subseteq F$
, we have ord
 $_{s=\omega } \; L(E/D,s) \leq $
ord
$_{s=\omega } \; L(E/D,s) \leq $
ord
 $_{s=\omega } \; L(E/F,s)$
. Thus, for any character
$_{s=\omega } \; L(E/F,s)$
. Thus, for any character
 $\chi $
with a pole at
$\chi $
with a pole at
 $s=\omega $
, one can consider
$s=\omega $
, one can consider
 $D=F^{\ker \chi }$
, the fixed field of
$D=F^{\ker \chi }$
, the fixed field of
 $\ker \chi $
. Thus, the conditions of the hypothesis for the counterexample carries over to
$\ker \chi $
. Thus, the conditions of the hypothesis for the counterexample carries over to
 $D , \; G / \ker \chi $
and
$D , \; G / \ker \chi $
and
 $ K$
. By minimality of
$ K$
. By minimality of
 $|G|$
, we must have
$|G|$
, we must have
 $\ker \chi $
=
$\ker \chi $
=
 $\{1\}$
.
$\{1\}$
. -
Step 2 : For all proper subgroups H of G,
 $\theta _{H}$
is a character of H.
$\theta _{H}$
is a character of H.We have the factorization
 $$ \begin{align*}L(E/F, s) = \prod \limits_{\chi \; \in \; \text{Irr}(G)} L(E/K \otimes \chi, s)^{\chi(1)}.\end{align*} $$
$$ \begin{align*}L(E/F, s) = \prod \limits_{\chi \; \in \; \text{Irr}(G)} L(E/K \otimes \chi, s)^{\chi(1)}.\end{align*} $$
Thus ord
 $_{s=\omega } L(E/F, s) = r = \sum _{\chi \; \in \; \text {Irr}(G)} n_{\chi } \chi (1) = \theta _G(1)$
. Suppose
$_{s=\omega } L(E/F, s) = r = \sum _{\chi \; \in \; \text {Irr}(G)} n_{\chi } \chi (1) = \theta _G(1)$
. Suppose
 $\psi $
is an irreducible character of H. Consider the L-series
$\psi $
is an irreducible character of H. Consider the L-series
 $L(E/F^H \otimes \psi , s)$
. By Proposition 4.5, we have
$L(E/F^H \otimes \psi , s)$
. By Proposition 4.5, we have
 $\theta _G |_H = \theta _{H}$
and so
$\theta _G |_H = \theta _{H}$
and so
 $\theta _{H}(1)= \theta _{G}|_H(1)=r$
. Thus, if
$\theta _{H}(1)= \theta _{G}|_H(1)=r$
. Thus, if
 $\omega $
is a pole, the triple
$\omega $
is a pole, the triple
 $F, \; H, \; F^H $
forms a counterexample contradicting minimality. Thus, for every irreducible character
$F, \; H, \; F^H $
forms a counterexample contradicting minimality. Thus, for every irreducible character
 $\psi $
of H,
$\psi $
of H,
 $L(E/F^H \otimes \psi , s)$
is analytic at
$L(E/F^H \otimes \psi , s)$
is analytic at
 $s=\omega $
, in particular,
$s=\omega $
, in particular,
 $n_{\psi } \geq 0$
which implies
$n_{\psi } \geq 0$
which implies
 $\theta _{H}$
is a character. Note that, by assumption,
$\theta _{H}$
is a character. Note that, by assumption,
 $\theta _{G}$
is not a character.
$\theta _{G}$
is not a character. -
Step 3 : Any irreducible
 $\chi $
of G with
$\chi $
of G with
 $n_{\chi } <0$
, is not induced from any proper subgroup of G.
$n_{\chi } <0$
, is not induced from any proper subgroup of G.Suppose
 $\chi = $
Ind
$\chi = $
Ind
 $_H^G \psi $
for a character
$_H^G \psi $
for a character
 $\psi $
of a proper subgroup H of G. Then
$\psi $
of a proper subgroup H of G. Then  $$ \begin{align*}L(E/K \otimes \chi,s) = L(E/F^H \otimes \psi, s) = \prod_{\phi} L(E/F^H \otimes \phi, s)^{a_{\phi}},\end{align*} $$
$$ \begin{align*}L(E/K \otimes \chi,s) = L(E/F^H \otimes \psi, s) = \prod_{\phi} L(E/F^H \otimes \phi, s)^{a_{\phi}},\end{align*} $$
where characters
 $\phi $
are the irreducible constituents of
$\phi $
are the irreducible constituents of
 $\psi $
with coefficient
$\psi $
with coefficient
 $a_{\phi }$
. By the previous step, since H is a proper subgroup, the factors are analytic at
$a_{\phi }$
. By the previous step, since H is a proper subgroup, the factors are analytic at
 $s=\omega $
, in particular,
$s=\omega $
, in particular,
 $ L(E/F^H \otimes \psi , s)$
is analytic at
$ L(E/F^H \otimes \psi , s)$
is analytic at
 $s=\omega $
contradicting
$s=\omega $
contradicting
 $n_{\chi } < 0$
.
$n_{\chi } < 0$
. -
Step 4 : There are no faithful characters of G of degree
 $\leq p_2-2$
. In particular, if
$\leq p_2-2$
. In particular, if
 $\chi $
is an irreducible character of G with
$\chi $
is an irreducible character of G with
 $n_{\chi }<0$
, then
$n_{\chi }<0$
, then
 $\chi (1)> p_2 - 2$
.
$\chi (1)> p_2 - 2$
.If G has a faithful character of degree
 $\leq p_2-2$
, then by Ito’s Theorem 4.7, G will have normal abelian Sylow
$\leq p_2-2$
, then by Ito’s Theorem 4.7, G will have normal abelian Sylow
 $p_i$
-subgroups for all prime factors
$p_i$
-subgroups for all prime factors
 $p_i, \; i \geq 2$
, of G. Also, all of them will be central and hence index of
$p_i, \; i \geq 2$
, of G. Also, all of them will be central and hence index of
 $Z(G)$
in G will be a power of
$Z(G)$
in G will be a power of
 $p_1$
. In particular,
$p_1$
. In particular,
 $G/Z(G)$
will be nilpotent and hence G will be nilpotent contradicting the existence of
$G/Z(G)$
will be nilpotent and hence G will be nilpotent contradicting the existence of
 $\chi $
.
$\chi $
.Note that, this in particular implies G must be non-abelian.
-
Step 5 : We now decompose
 $\theta _G$
into three constituents
$\theta _G$
into three constituents
 $\theta _{nf}, \; \theta _{+}$
, and
$\theta _{nf}, \; \theta _{+}$
, and
 $\theta _{-}$
as follows:
$\theta _{-}$
as follows:-
•
 $\theta _{nf}$
is the sum of all constituents
$\theta _{nf}$
is the sum of all constituents
 $n_{\lambda } \lambda $
of
$n_{\lambda } \lambda $
of
 $\theta _G$
such that
$\theta _G$
such that
 $\lambda $
is an irreducible character of G that is not faithful (hence the “
$\lambda $
is an irreducible character of G that is not faithful (hence the “
 $nf$
” ).
$nf$
” ). -
•
 $\theta _+$
is the sum of all constituents
$\theta _+$
is the sum of all constituents
 $n_{\psi } \psi $
of
$n_{\psi } \psi $
of
 $\theta _G$
such that
$\theta _G$
such that
 $\psi $
is an irreducible character of G that is faithful and
$\psi $
is an irreducible character of G that is faithful and
 $n_{\psi }>0$
.
$n_{\psi }>0$
. -
•
 $\theta _- = \sum (- n_{\chi }) \chi $
, where
$\theta _- = \sum (- n_{\chi }) \chi $
, where
 $n_{\chi } \chi $
are all those constituents of
$n_{\chi } \chi $
are all those constituents of
 $\theta _G$
such that
$\theta _G$
such that
 $\chi $
is an irreducible character of G that is faithful and
$\chi $
is an irreducible character of G that is faithful and
 $n_{\chi }<0$
.
$n_{\chi }<0$
.
From Step 1, all the coefficients of
 $\theta _{nf}$
are nonnegative. Thus
$\theta _{nf}$
are nonnegative. Thus
 $\theta _{nf}$
is either a character or 0. By construction
$\theta _{nf}$
is either a character or 0. By construction
 $\theta _{-}$
is a character (since there is at least one irreducible character
$\theta _{-}$
is a character (since there is at least one irreducible character
 $\chi $
with
$\chi $
with
 $n_{\chi } <0$
) and
$n_{\chi } <0$
) and
 $\theta _{+}$
is either a character or 0. Also note that, by construction,
$\theta _{+}$
is either a character or 0. Also note that, by construction,
 $ \langle \theta _{nf}, \theta _{-} \rangle = 0$
, as well as
$ \langle \theta _{nf}, \theta _{-} \rangle = 0$
, as well as
 $\langle \theta _{+}, \theta _{-} \rangle = 0$
and
$\langle \theta _{+}, \theta _{-} \rangle = 0$
and
 $\langle \theta _{+}, \theta _{nf} \rangle = 0$
and
$\langle \theta _{+}, \theta _{nf} \rangle = 0$
and  $$ \begin{align*}\theta_{G} = \theta_{nf} - \theta_{-} + \theta_{+}.\end{align*} $$
$$ \begin{align*}\theta_{G} = \theta_{nf} - \theta_{-} + \theta_{+}.\end{align*} $$
The final contradiction will come from showing
 $\theta _{+} = \theta _{-}$
.
$\theta _{+} = \theta _{-}$
. -
-
Step 6 : In any finite group X, every normal subgroup appears as one of the subgroups in a chief series
 $X=X_1 \geq X_2 \geq \cdots \geq X_{n-1} \geq X_n=\{1\}$
, where each
$X=X_1 \geq X_2 \geq \cdots \geq X_{n-1} \geq X_n=\{1\}$
, where each
 $X_i \trianglelefteq G$
. In particular, for our solvable G the chief factors
$X_i \trianglelefteq G$
. In particular, for our solvable G the chief factors
 $G_i/G_{i+1}$
are elementary abelian p-groups (see [Reference Isaacs Martin14, Corollary 8.7, p. 102]). In particular, the last chief factor
$G_i/G_{i+1}$
are elementary abelian p-groups (see [Reference Isaacs Martin14, Corollary 8.7, p. 102]). In particular, the last chief factor
 $G_{n-1}/\{1\}$
is a nontrivial abelian group. That is, every normal subgroup of G contains a nontrivial abelian p-group that is normal in G. We have already seen that every abelian normal subgroup of G is central. Thus for every irreducible character
$G_{n-1}/\{1\}$
is a nontrivial abelian group. That is, every normal subgroup of G contains a nontrivial abelian p-group that is normal in G. We have already seen that every abelian normal subgroup of G is central. Thus for every irreducible character
 $\lambda $
of G that is not faithful,
$\lambda $
of G that is not faithful,
 $\ker \lambda \cap Z(G) \neq 1$
. By Proposition 4.8, G has a normal subgroup
$\ker \lambda \cap Z(G) \neq 1$
. By Proposition 4.8, G has a normal subgroup
 $N\supseteq Z(G)$
of prime index, say p.
$N\supseteq Z(G)$
of prime index, say p. -
Step 7 :
 $\;\; \langle \theta _{-}|_N, \theta _{nf}|_N \rangle _N = 0 $
$\;\; \langle \theta _{-}|_N, \theta _{nf}|_N \rangle _N = 0 $
First, we note that
 $\chi |_N$
is irreducible for every irreducible constituent
$\chi |_N$
is irreducible for every irreducible constituent
 $\chi $
of
$\chi $
of
 $\theta _-$
. Since, if not, then from Proposition 4.9, we have
$\theta _-$
. Since, if not, then from Proposition 4.9, we have
 $\chi |_N = \psi _1 + \cdots + \psi _p$
for some irreducible characters
$\chi |_N = \psi _1 + \cdots + \psi _p$
for some irreducible characters
 $\psi _i$
of N and
$\psi _i$
of N and
 $\chi = $
Ind
$\chi = $
Ind
 $_H^G \psi _1$
, contradicting Step 3. Now for any irreducible constituent
$_H^G \psi _1$
, contradicting Step 3. Now for any irreducible constituent
 $\lambda $
of
$\lambda $
of
 $\theta _{nf}$
, we have seen
$\theta _{nf}$
, we have seen
 $\ker \lambda \cap Z(G) \neq \{1\} $
, i.e.,
$\ker \lambda \cap Z(G) \neq \{1\} $
, i.e.,
 $\lambda |_N$
is not faithful as
$\lambda |_N$
is not faithful as
 $N \supseteq Z(G)$
. Again by Proposition 4.9, either
$N \supseteq Z(G)$
. Again by Proposition 4.9, either
 $\lambda |_N$
is irreducible, or is induced from irreducible constituents, thus they are also not faithful. Hence
$\lambda |_N$
is irreducible, or is induced from irreducible constituents, thus they are also not faithful. Hence
 $ \langle \theta _{-}|_N, \theta _{nf}|_N \rangle _N = 0 .$
$ \langle \theta _{-}|_N, \theta _{nf}|_N \rangle _N = 0 .$
-
Step 8 :
 $\theta _{+}|_N = \theta _{-}|_N $
$\theta _{+}|_N = \theta _{-}|_N $
By Step 2,
 $\theta _{N}$
is a character. Also, by Proposition 4.5,
$\theta _{N}$
is a character. Also, by Proposition 4.5,
 $\theta _{N} = \theta _{G}|_N = \theta _{+}|_N - \theta _{-}|_N + \theta _{nf}|_N$
. Therefore, by Step 7, either
$\theta _{N} = \theta _{G}|_N = \theta _{+}|_N - \theta _{-}|_N + \theta _{nf}|_N$
. Therefore, by Step 7, either
 $\theta _{+}|_N = \theta _{-}|_N$
or
$\theta _{+}|_N = \theta _{-}|_N$
or
 $\theta _{+}|_N = \theta _{-}|_N + \phi $
for some character
$\theta _{+}|_N = \theta _{-}|_N + \phi $
for some character
 $\phi $
of N. Assume the latter, then (4.1)Let
$\phi $
of N. Assume the latter, then (4.1)Let $$ \begin{align} r = \theta_{G}(1) = \theta_{G}|_N(1) = \phi(1) + \theta_{nf}(1). \end{align} $$
$$ \begin{align} r = \theta_{G}(1) = \theta_{G}|_N(1) = \phi(1) + \theta_{nf}(1). \end{align} $$
 $\phi _1$
be an irreducible constituent of
$\phi _1$
be an irreducible constituent of
 $\phi $
, and hence of
$\phi $
, and hence of
 $\theta _{+}|_N$
. If
$\theta _{+}|_N$
. If
 $\psi $
is an irreducible constituent of
$\psi $
is an irreducible constituent of
 $\theta _{+}$
such that
$\theta _{+}$
such that
 $\phi _1$
occurs in
$\phi _1$
occurs in
 $\psi |_N$
, we see that
$\psi |_N$
, we see that
 $\psi |_N \neq \phi _1$
. This is because
$\psi |_N \neq \phi _1$
. This is because
 $\phi _1(1) \leq r$
by (4.1), where as
$\phi _1(1) \leq r$
by (4.1), where as
 $\psi $
being faithful,
$\psi $
being faithful,
 $\psi |_N(1)> p_2-1 \geq r$
by Step 4. Applying Proposition 4.9 again,
$\psi |_N(1)> p_2-1 \geq r$
by Step 4. Applying Proposition 4.9 again,
 $\psi _{N} = \phi _1 + \cdots + \phi _p$
. These are distinct G-conjugate irreducible characters of N. Since,
$\psi _{N} = \phi _1 + \cdots + \phi _p$
. These are distinct G-conjugate irreducible characters of N. Since,
 $\phi _1$
is an irreducible constituent of
$\phi _1$
is an irreducible constituent of
 $\phi $
and
$\phi $
and
 $\phi = (\theta _{+} - \theta _{-})|_N$
is a G-stable character of N, each
$\phi = (\theta _{+} - \theta _{-})|_N$
is a G-stable character of N, each
 $\phi _i$
must also appear as a constituent of
$\phi _i$
must also appear as a constituent of
 $\phi $
. Thus, we have
$\phi $
. Thus, we have
 $\psi (1) = \phi _1(1)+ \cdots + \phi _p(1) \leq \phi (1) \leq r.$
This contradicts
$\psi (1) = \phi _1(1)+ \cdots + \phi _p(1) \leq \phi (1) \leq r.$
This contradicts
 $\psi (1) = \psi |_N(1)> r$
computed above, thus
$\psi (1) = \psi |_N(1)> r$
computed above, thus
 $\theta _{+}|_N = \theta _{-}|_N $
.
$\theta _{+}|_N = \theta _{-}|_N $
.
-
Final Step : Let
 $g \in G \setminus N$
, and let H be the subgroup generated by g and
$g \in G \setminus N$
, and let H be the subgroup generated by g and
 $Z(G)$
. Since, H is abelian,
$Z(G)$
. Since, H is abelian,
 $H \neq G$
. Let
$H \neq G$
. Let
 $\lambda $
be a constituent of
$\lambda $
be a constituent of
 $\theta _{nf}$
, then from Step 6, we have
$\theta _{nf}$
, then from Step 6, we have
 $\ker \lambda \cap Z(G)\neq \{1\}$
. Thus, the same holds for Ind
$\ker \lambda \cap Z(G)\neq \{1\}$
. Thus, the same holds for Ind
 $_H^G(\lambda |_H)$
. Let
$_H^G(\lambda |_H)$
. Let
 $\chi $
be an irreducible constituent of
$\chi $
be an irreducible constituent of
 $\theta _{-}$
, hence is faithful and so
$\theta _{-}$
, hence is faithful and so
 $\langle \chi ,$
Ind
$\langle \chi ,$
Ind
 $_H^G(\lambda |_H) \rangle = 0$
. Hence by Frobenius reciprocity,
$_H^G(\lambda |_H) \rangle = 0$
. Hence by Frobenius reciprocity,
 $\langle \chi |_H, \lambda |_H \rangle = 0$
and so, like in Step 7,
$\langle \chi |_H, \lambda |_H \rangle = 0$
and so, like in Step 7,
 $\langle \theta _{-}|_H, \theta _{nf}|_H \rangle _H = 0$
. Now
$\langle \theta _{-}|_H, \theta _{nf}|_H \rangle _H = 0$
. Now
 $\theta _H = \theta _{G}|_H = \theta _{+}|_H - \theta _{-}|_H + \theta _{nf}|_H$
. As before, either
$\theta _H = \theta _{G}|_H = \theta _{+}|_H - \theta _{-}|_H + \theta _{nf}|_H$
. As before, either
 $\theta _{+}|_H - \theta _{-}|_H$
is zero or a character and arguing in the exact same way as Step 8, we get
$\theta _{+}|_H - \theta _{-}|_H$
is zero or a character and arguing in the exact same way as Step 8, we get
 $\theta _{+}|_H = \theta _{-}|_H$
. Hence,
$\theta _{+}|_H = \theta _{-}|_H$
. Hence,
 $\theta _{+}(g) = \theta _{-}(g)$
for all
$\theta _{+}(g) = \theta _{-}(g)$
for all
 $g \in G \setminus N$
. Combining this with Step 8, gives
$g \in G \setminus N$
. Combining this with Step 8, gives
 $\theta _{+} = \theta _{-}$
. This is a contradiction and hence the theorem is proved.
$\theta _{+} = \theta _{-}$
. This is a contradiction and hence the theorem is proved.
5 Elliptic analogue of Foote and Wales’s Theorem
Theorem 5.1 Let
![]() $E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
$E/K$
be an elliptic curve and suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group
![]() $G=$
$G=$
![]() $\mathrm{Gal}(F/K)$
. Let
$\mathrm{Gal}(F/K)$
. Let
![]() $\chi $
be an irreducible character of G. Then,
$\chi $
be an irreducible character of G. Then,
![]() $L(E/K \otimes \chi , s)$
is holomorphic at
$L(E/K \otimes \chi , s)$
is holomorphic at
![]() $s = \omega $
, if
$s = \omega $
, if
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F, s)$
of order
$L(E/F, s)$
of order
![]() $ \leq 2$
.
$ \leq 2$
.
The proof of this theorem follows its counterpart more directly than the previous one, because of the following theorem.
Theorem 5.2
(Foote–Wales) Let G be a finite group with a virtual character
![]() $\theta $
satisfying the following conditions:
$\theta $
satisfying the following conditions:
-
(1)
 $\theta (1) \leq 2$
,
$\theta (1) \leq 2$
, -
(2)
 $\theta $
is not a character of G but
$\theta $
is not a character of G but
 $\theta |_H$
is a character for every proper subgroup H of
$\theta |_H$
is a character for every proper subgroup H of
 $G,$
and
$G,$
and -
(3) if
 $\chi $
is any irreducible constituent of
$\chi $
is any irreducible constituent of
 $\theta $
such that
$\theta $
such that
 $\langle \theta , \chi \rangle < 0$
, then
$\langle \theta , \chi \rangle < 0$
, then
 $\chi $
is faithful, nonlinear and is not induced from any proper subgroup of G.
$\chi $
is faithful, nonlinear and is not induced from any proper subgroup of G.
Then
![]() $\theta (1) = 2$
and
$\theta (1) = 2$
and
![]() $G \cong \operatorname {\mathrm {SL}}_2(p)$
, for some prime
$G \cong \operatorname {\mathrm {SL}}_2(p)$
, for some prime
![]() $p \geq 5$
, or
$p \geq 5$
, or
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
.
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
.
Note that in their notation,
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
denotes any nontrivial semidirect product of
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
denotes any nontrivial semidirect product of
![]() $Q_8$
(the quaternion group of order
$Q_8$
(the quaternion group of order
![]() $8$
) by a cyclic 3-group. For a proof, see [Reference Foote and Wales10, Theorem III].
$8$
) by a cyclic 3-group. For a proof, see [Reference Foote and Wales10, Theorem III].
Additionally, we are assuming that G is solvable and so G cannot be
![]() $\operatorname {\mathrm {SL}}_2(p)$
(
$\operatorname {\mathrm {SL}}_2(p)$
(
![]() $p \geq 5$
). For
$p \geq 5$
). For
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
, Foote and Wales in [Reference Foote and Wales10, p. 229] tackles this possibility by quoting a deep result of Langlands which shows that Artin’s holomorphy conjecture is true in the case when
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
, Foote and Wales in [Reference Foote and Wales10, p. 229] tackles this possibility by quoting a deep result of Langlands which shows that Artin’s holomorphy conjecture is true in the case when
![]() $G/Z(G) \cong A_4$
. We address this in our next proposition. The proof can be seen as consequence of a result of Wong (see [Reference Wong30, Theorem 1.3]). But for the sake of completeness, we present it here.
$G/Z(G) \cong A_4$
. We address this in our next proposition. The proof can be seen as consequence of a result of Wong (see [Reference Wong30, Theorem 1.3]). But for the sake of completeness, we present it here.
Proposition 5.3 Suppose that E satisfies the generalized Taniyama conjecture over K. Let F be a Galois extension of K with solvable Galois group isomorphic to
![]() $ \widehat {\operatorname {\mathrm {SL}}_2}(3)$
. Let
$ \widehat {\operatorname {\mathrm {SL}}_2}(3)$
. Let
![]() $\chi $
be an irreducible character of G. Then,
$\chi $
be an irreducible character of G. Then,
![]() $L(E/K \otimes \chi , s)$
is automorphic and hence entire.
$L(E/K \otimes \chi , s)$
is automorphic and hence entire.
Proof Note that
![]() $Q_8 \unlhd \widehat {\operatorname {\mathrm {SL}}_2}(3)$
and the quotient is a 3-group, in particular, is nilpotent. A result of Horváth (see [Reference Horváth, Campbell, Hurley, Robertson, Tobin and Ward12, Proposition 2.7]) says that this makes
$Q_8 \unlhd \widehat {\operatorname {\mathrm {SL}}_2}(3)$
and the quotient is a 3-group, in particular, is nilpotent. A result of Horváth (see [Reference Horváth, Campbell, Hurley, Robertson, Tobin and Ward12, Proposition 2.7]) says that this makes
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
an “SM-group relative to
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
an “SM-group relative to
![]() $Q_8$
.” What this means in our context, is that, every irreducible character
$Q_8$
.” What this means in our context, is that, every irreducible character
![]() $\chi $
of
$\chi $
of
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
, is induced from an irreducible character
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
, is induced from an irreducible character
![]() $\psi $
of a subnormal subgroup H containing
$\psi $
of a subnormal subgroup H containing
![]() $Q_8$
. Moreover,
$Q_8$
. Moreover,
![]() $\psi |_{Q_8} $
is irreducible and hence
$\psi |_{Q_8} $
is irreducible and hence
![]() ${\psi (1) = \psi |_{Q_8}(1) \leq 2}$
. Further note that, in the degree
${\psi (1) = \psi |_{Q_8}(1) \leq 2}$
. Further note that, in the degree
![]() $2$
case,
$2$
case,
![]() $\psi $
can not be the icosahedral type (recall, this is the case when the image of the degree
$\psi $
can not be the icosahedral type (recall, this is the case when the image of the degree
![]() $2$
representation in PGL
$2$
representation in PGL
![]() $_2(\mathbb {C})$
is isomorphic to
$_2(\mathbb {C})$
is isomorphic to
![]() $A_5$
). This is because, the only prime factors of
$A_5$
). This is because, the only prime factors of
![]() $ \widehat {\operatorname {\mathrm {SL}}_2}(3)$
, and hence of H, are
$ \widehat {\operatorname {\mathrm {SL}}_2}(3)$
, and hence of H, are
![]() $2$
and
$2$
and
![]() $3$
. In particular,
$3$
. In particular,
![]() $5$
is not a prime factor of H.
$5$
is not a prime factor of H.
Now if
![]() $\psi $
is of degree 1, then, from Artin reciprocity,
$\psi $
is of degree 1, then, from Artin reciprocity,
![]() $\psi $
can be seen as an idèle class character. If
$\psi $
can be seen as an idèle class character. If
![]() $\psi $
is of degree 2, from theorems of Langlands and Tunnell (see [Reference Langlands18, Reference Tunnell28]),
$\psi $
is of degree 2, from theorems of Langlands and Tunnell (see [Reference Langlands18, Reference Tunnell28]),
![]() $\psi $
is associated with a cuspidal automorphic representation
$\psi $
is associated with a cuspidal automorphic representation
![]() $\pi _{\psi }$
of
$\pi _{\psi }$
of
![]() $\operatorname {\mathrm {GL}}_2(\mathbb {A}_{K^H} )$
. Since H is subnormal, there exists a subnormal series
$\operatorname {\mathrm {GL}}_2(\mathbb {A}_{K^H} )$
. Since H is subnormal, there exists a subnormal series
Moreover, since we assumed solvability,
![]() $H_{i+1}/H_i$
is of prime degree. Therefore, by repeated application of Arthur and Clozel’s theory of base change for cyclic extensions (see [Reference Arthur and Clozel2, Theorem 4.2]), the base change map
$H_{i+1}/H_i$
is of prime degree. Therefore, by repeated application of Arthur and Clozel’s theory of base change for cyclic extensions (see [Reference Arthur and Clozel2, Theorem 4.2]), the base change map
![]() $B(\pi ) \in \operatorname {\mathrm {GL}}_2(\mathbb {A}_{K^H})$
exists. Recall, we are writing,
$B(\pi ) \in \operatorname {\mathrm {GL}}_2(\mathbb {A}_{K^H})$
exists. Recall, we are writing,
![]() $L(E/K, s) = L(\pi , s)$
. For a short exposition on the base change map, see [Reference Murty and Kumar Murty21, Section 3], we’re following their notation. Now
$L(E/K, s) = L(\pi , s)$
. For a short exposition on the base change map, see [Reference Murty and Kumar Murty21, Section 3], we’re following their notation. Now
Since functoriality is known in cases of
![]() $\operatorname {\mathrm {GL}}(n) \times \operatorname {\mathrm {GL}}(1)$
and
$\operatorname {\mathrm {GL}}(n) \times \operatorname {\mathrm {GL}}(1)$
and
![]() $\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(2)$
, the latter due to Ramakrishnan [Reference Ramakrishnan22], and we saw that either
$\operatorname {\mathrm {GL}}(2) \times \operatorname {\mathrm {GL}}(2)$
, the latter due to Ramakrishnan [Reference Ramakrishnan22], and we saw that either
![]() $\psi $
is an idèle class character or an automorphic representation of
$\psi $
is an idèle class character or an automorphic representation of
![]() $\operatorname {\mathrm {GL}}(2)$
, so
$\operatorname {\mathrm {GL}}(2)$
, so
![]() $L(E/K \otimes \chi , s)$
is automorphic and hence entire.
$L(E/K \otimes \chi , s)$
is automorphic and hence entire.
5.1 Proof of Theorem 5.1
As in Theorem 4.1, assume the statement is false and take a counterexample
![]() $F/K$
with
$F/K$
with
![]() $[F:K]$
minimal. Thus, there exists an irreducible character
$[F:K]$
minimal. Thus, there exists an irreducible character
![]() $\psi $
of
$\psi $
of
![]() $G =$
Gal
$G =$
Gal
![]() $(F/K)$
and a point
$(F/K)$
and a point
![]() $s=\omega $
such that
$s=\omega $
such that
![]() $\omega $
is a zero of
$\omega $
is a zero of
![]() $L(E/F,s)$
of order
$L(E/F,s)$
of order
![]() $\leq 2$
but
$\leq 2$
but
![]() $L(E/K \otimes \psi , s)$
has a pole at
$L(E/K \otimes \psi , s)$
has a pole at
![]() $s=\omega $
.
$s=\omega $
.
Set
![]() $\theta = \theta _G = \sum n_{\chi } \chi $
. Note that
$\theta = \theta _G = \sum n_{\chi } \chi $
. Note that
![]() $n_{\psi } < 0$
. Since we have the factorization
$n_{\psi } < 0$
. Since we have the factorization
so,
![]() $\theta _G(1) = \sum _{\chi \; \in \; \text {Irr}(G)} n_{\chi } \chi (1) =$
ord
$\theta _G(1) = \sum _{\chi \; \in \; \text {Irr}(G)} n_{\chi } \chi (1) =$
ord
![]() $_{s=\omega } L(E/F, s) \leq 2$
. Moreover, we can then carry out Steps 1–4, as it is, in the proof of Theorem 4.1. Hence, all the conditions of Theorem 5.2 are satisfied. But then the solvability assumption eliminates
$_{s=\omega } L(E/F, s) \leq 2$
. Moreover, we can then carry out Steps 1–4, as it is, in the proof of Theorem 4.1. Hence, all the conditions of Theorem 5.2 are satisfied. But then the solvability assumption eliminates
![]() $\operatorname {\mathrm {SL}}_2(p)$
and Proposition 5.3 eliminates
$\operatorname {\mathrm {SL}}_2(p)$
and Proposition 5.3 eliminates
![]() $\widehat {\operatorname {\mathrm {SL}}_2}(3)$
giving us a contradiction.
$\widehat {\operatorname {\mathrm {SL}}_2}(3)$
giving us a contradiction.
6 Applications to minimal subfields
We now look at some applications of our theorems in the context of analytic and algebraic minimal subfields.
Theorem 6.1 Let
![]() $E/K$
be an elliptic curve, and let
$E/K$
be an elliptic curve, and let
![]() $F/K$
be a finite Galois extension with solvable Galois group
$F/K$
be a finite Galois extension with solvable Galois group
![]() $G=$
$G=$
![]() $\mathrm{Gal}(F/K)$
. Suppose that E satisfies the generalized Taniyama conjecture over K and
$\mathrm{Gal}(F/K)$
. Suppose that E satisfies the generalized Taniyama conjecture over K and
![]() $L(E/F,s)$
has a zero at
$L(E/F,s)$
has a zero at
![]() $\omega $
of order two. Then the analytic minimal subfield
$\omega $
of order two. Then the analytic minimal subfield
![]() $F_{\omega }$
exists. Further, if
$F_{\omega }$
exists. Further, if
![]() $\omega $
is real, then
$\omega $
is real, then
![]() $G=$
$G=$
![]() $\mathrm{Gal}(F_{\omega }/K)$
satisfies one of the following:
$\mathrm{Gal}(F_{\omega }/K)$
satisfies one of the following:
-
(i) G is either cyclic or dihedral.
-
(ii)
 $Z(G) \cong {\mathbb Z}/2{\mathbb Z}$
and
$Z(G) \cong {\mathbb Z}/2{\mathbb Z}$
and
 $G/Z(G) \cong D_{2n}, A_4 $
or,
$G/Z(G) \cong D_{2n}, A_4 $
or,
 $S_4$
.
$S_4$
.
Proof By Theorem 5.1,
![]() $L(E/K \otimes \chi , s)$
is holomorphic for every irreducible character
$L(E/K \otimes \chi , s)$
is holomorphic for every irreducible character
![]() $\chi $
of G. Hence, by Proposition 3.1,
$\chi $
of G. Hence, by Proposition 3.1,
![]() $F_{\omega }$
exists.
$F_{\omega }$
exists.
Now suppose
![]() $\omega $
is real. We have the factorization
$\omega $
is real. We have the factorization
Since ord
![]() $_{s=\omega } \; L(E/F,s)=2$
, then there exists
$_{s=\omega } \; L(E/F,s)=2$
, then there exists
![]() $\chi \in $
Irr
$\chi \in $
Irr
![]() $(G)$
such that ord
$(G)$
such that ord
![]() $_{s=\omega } \; L(E/K \otimes \chi , s) \geq 1$
. Since
$_{s=\omega } \; L(E/K \otimes \chi , s) \geq 1$
. Since
![]() $\omega $
is real, we have
$\omega $
is real, we have
Case I :
![]() $\chi \neq \overline {\chi }$
. Hence
$\chi \neq \overline {\chi }$
. Hence
![]() $\chi (1) = 1 = \overline {\chi }(1)$
. Thus,
$\chi (1) = 1 = \overline {\chi }(1)$
. Thus,
![]() $\chi $
is one-dimensional. Then
$\chi $
is one-dimensional. Then
![]() $F_{\omega }$
, being the fixed field of
$F_{\omega }$
, being the fixed field of
![]() $\ker \chi \; \cap \ker \overline {\chi } = \ker \chi $
, is cyclic.
$\ker \chi \; \cap \ker \overline {\chi } = \ker \chi $
, is cyclic.
Case II :
![]() $\chi = \overline {\chi }$
and
$\chi = \overline {\chi }$
and
![]() $\chi (1) = 1$
. Thus,
$\chi (1) = 1$
. Thus,
![]() $\chi $
is a real irreducible linear character. Since the order of vanishing of
$\chi $
is a real irreducible linear character. Since the order of vanishing of
![]() $L(E/F,s)$
at
$L(E/F,s)$
at
![]() $\omega $
is 2, there exists another such character. Hence, Gal
$\omega $
is 2, there exists another such character. Hence, Gal
![]() $(F_{\omega })/K$
is a subgroup of
$(F_{\omega })/K$
is a subgroup of
![]() ${\mathbb Z}_2 \oplus {\mathbb Z}_2$
.
${\mathbb Z}_2 \oplus {\mathbb Z}_2$
.
Case III :
![]() $\chi = \overline {\chi }$
and
$\chi = \overline {\chi }$
and
![]() $\chi (1) = 2$
. Since
$\chi (1) = 2$
. Since
![]() $F_{\omega }$
is the fixed field of
$F_{\omega }$
is the fixed field of
![]() $\ker \chi $
, Gal
$\ker \chi $
, Gal
![]() $(F_{\omega }/K)$
admits a faithful degree 2 irreducible representation coming from the quotient representation corresponding to
$(F_{\omega }/K)$
admits a faithful degree 2 irreducible representation coming from the quotient representation corresponding to
![]() $\chi $
. Let the character of this representation be denoted by
$\chi $
. Let the character of this representation be denoted by
![]() $\tilde {\chi }$
. Therefore, we know that
$\tilde {\chi }$
. Therefore, we know that
![]() $G/Z(G)$
is isomorphic to a finite subgroup of PGL
$G/Z(G)$
is isomorphic to a finite subgroup of PGL
![]() $_2(\mathbb {C})$
and therefore is isomorphic to
$_2(\mathbb {C})$
and therefore is isomorphic to
![]() $C_n, D_{n}, A_4, S_4,$
or
$C_n, D_{n}, A_4, S_4,$
or
![]() $A_5$
(see [Reference Serre24, Proposition 16 and Section 2.5]). By the solvability condition,
$A_5$
(see [Reference Serre24, Proposition 16 and Section 2.5]). By the solvability condition,
![]() $A_5$
can be eliminated. Since
$A_5$
can be eliminated. Since
![]() $\chi = \overline {\chi }$
, we have
$\chi = \overline {\chi }$
, we have
![]() $\tilde {\chi } = \overline {\tilde {\chi }}$
, and so
$\tilde {\chi } = \overline {\tilde {\chi }}$
, and so
![]() $Z(G) = \{1\}$
or
$Z(G) = \{1\}$
or
![]() ${\mathbb Z}/2{\mathbb Z}$
. Now
${\mathbb Z}/2{\mathbb Z}$
. Now
![]() $G/Z(G)$
cannot be cyclic as that will imply G is abelian. Note that when
$G/Z(G)$
cannot be cyclic as that will imply G is abelian. Note that when
![]() $Z(G) = \{1\}$
, then the only possibilities are
$Z(G) = \{1\}$
, then the only possibilities are
![]() $D_{2n}$
and
$D_{2n}$
and
![]() $S_4$
. (This is because
$S_4$
. (This is because
![]() $A_4$
does not have any two-dimensional irreducible representations.) Moreover, if
$A_4$
does not have any two-dimensional irreducible representations.) Moreover, if
![]() $G \cong S_4$
, then, by [Reference Serre25, Proposition 24, p. 61] (take
$G \cong S_4$
, then, by [Reference Serre25, Proposition 24, p. 61] (take
![]() $A=A_4$
), there are two possibilities. We show that both of them lead to contradictions. Suppose
$A=A_4$
), there are two possibilities. We show that both of them lead to contradictions. Suppose
![]() $\tilde {\chi }|_{A_4}$
is isotypic (i.e., it is a direct sum of isomorphic irreducible representations). Since
$\tilde {\chi }|_{A_4}$
is isotypic (i.e., it is a direct sum of isomorphic irreducible representations). Since
![]() $A_4$
does not have any two-dimensional irreducible representation,
$A_4$
does not have any two-dimensional irreducible representation,
![]() $\tilde {\chi }|_{A_4}$
is also reducible and isotypic and so,
$\tilde {\chi }|_{A_4}$
is also reducible and isotypic and so,
![]() $A_4 \subseteq Z(G)$
, a contradiction. Thus, there exists an irreducible representation
$A_4 \subseteq Z(G)$
, a contradiction. Thus, there exists an irreducible representation
![]() $\psi $
of
$\psi $
of
![]() $A_4$
such that
$A_4$
such that
![]() $\tilde {\chi } = $
Ind
$\tilde {\chi } = $
Ind
![]() $_{A_4}^{S_4} \psi $
with
$_{A_4}^{S_4} \psi $
with
![]() $\psi (1) = 1$
. But we also know that every representation of
$\psi (1) = 1$
. But we also know that every representation of
![]() $A_4$
of dimension 1 has
$A_4$
of dimension 1 has
![]() $V_4$
in its kernel, therefore,
$V_4$
in its kernel, therefore,
![]() $V_4 \subseteq \ker \psi $
. Since
$V_4 \subseteq \ker \psi $
. Since
![]() $V_4 \unlhd S_4$
, hence
$V_4 \unlhd S_4$
, hence
![]() $V_4 \subset \ker $
Ind
$V_4 \subset \ker $
Ind
![]() $_{A_4}^{S_4} \psi = \ker \tilde {\chi }$
, contradicting faithfulness of
$_{A_4}^{S_4} \psi = \ker \tilde {\chi }$
, contradicting faithfulness of
![]() $\tilde {\chi }$
.
$\tilde {\chi }$
.
We now look at more applications of our results in relation to the celebrated Birch and Swinnerton-Dyer conjecture. The BSD conjecture predicts that the rank of
![]() $E(K)$
is equal to the order of vanishing of
$E(K)$
is equal to the order of vanishing of
![]() $L(E/K,s)$
at
$L(E/K,s)$
at
![]() $s=1$
. Due to work of Gross and Zagier [Reference Gross and Zagier11] and Kolyvagin [Reference Kolyvagin17], this is known for
$s=1$
. Due to work of Gross and Zagier [Reference Gross and Zagier11] and Kolyvagin [Reference Kolyvagin17], this is known for
![]() $K= \mathbb {{\mathbb Q}}$
and ord
$K= \mathbb {{\mathbb Q}}$
and ord
![]() $_{s=1} L(E/ {\mathbb Q}, s) \leq 1$
. In the next theorem, we prove a slight generalization to this result, namely, we look at the case when rank increases by
$_{s=1} L(E/ {\mathbb Q}, s) \leq 1$
. In the next theorem, we prove a slight generalization to this result, namely, we look at the case when rank increases by
![]() $1$
in a solvable extension.
$1$
in a solvable extension.
Theorem 6.2 Let
![]() $E/ {\mathbb Q}$
be an elliptic curve, and let
$E/ {\mathbb Q}$
be an elliptic curve, and let
![]() $K/{\mathbb Q}$
be a solvable Galois extension.
$K/{\mathbb Q}$
be a solvable Galois extension.
-
(i) If
 ${\mathbf {rk}} E(K) = {\mathbf {rk}} E({\mathbb Q}) + 1$
, then ord
${\mathbf {rk}} E(K) = {\mathbf {rk}} E({\mathbb Q}) + 1$
, then ord
 $_{s=1} \; L(E/K,s) \geq $
ord
$_{s=1} \; L(E/K,s) \geq $
ord
 $_{s=1} \; L(E/{\mathbb Q},s) + 1$
.
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
. -
(ii) If
 $L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
$L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
 $s=1$
for every irreducible character
$s=1$
for every irreducible character
 $\chi $
of
$\chi $
of
 $\mathrm{Gal}(K/{\mathbb Q})$
, and ord
$\mathrm{Gal}(K/{\mathbb Q})$
, and ord
 $_{s=1} \; L(E/K,s) = $
ord
$_{s=1} \; L(E/K,s) = $
ord
 $_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
 $ {\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
$ {\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
In both cases, equality holds if the algebraic and the analytic minimal subfields are equal.
Proof (i) Let M be the algebraic minimal subfield. By Theorem 1.1, M is a quadratic extension of
![]() ${\mathbb Q}$
, say of discriminant D. Consider the twisted elliptic curve
${\mathbb Q}$
, say of discriminant D. Consider the twisted elliptic curve
![]() $E_D$
. Then we have
$E_D$
. Then we have
(see, e.g., [Reference Ireland and Rosen13, Proposition 20.5.4, p. 357]). Thus,
![]() ${\mathbf {rk}} E_D({\mathbb Q}) = 1 =$
ord
${\mathbf {rk}} E_D({\mathbb Q}) = 1 =$
ord
![]() $_{s=1} L(E_D/ {\mathbb Q},s)$
. We also have
$_{s=1} L(E_D/ {\mathbb Q},s)$
. We also have
![]() $L(E/M,s) = L(E/{\mathbb Q},s) \cdot L(E_D/ {\mathbb Q},s)$
. Thus,
$L(E/M,s) = L(E/{\mathbb Q},s) \cdot L(E_D/ {\mathbb Q},s)$
. Thus,
where the first inequality follows directly from Theorem 4.4. Note that equality holds if
![]() $M=F_{1}$
(the analytic minimal subfield at
$M=F_{1}$
(the analytic minimal subfield at
![]() $s=1$
).
$s=1$
).
(ii) The holomorphy condition ensures that the analytic minimal subfield exists. We have the factorization
Since the order of zero increases by 1, we see that there is a nontrivial character
![]() $\chi $
of degree 1 such that
$\chi $
of degree 1 such that
![]() $L(E/ {\mathbb Q} \otimes \chi , 1) = 0$
. Since the analytic minimal subfield
$L(E/ {\mathbb Q} \otimes \chi , 1) = 0$
. Since the analytic minimal subfield
![]() $F_{1}$
is the fixed field of
$F_{1}$
is the fixed field of
![]() $\ker \chi $
, thus it is cyclic. Moreover, as ord
$\ker \chi $
, thus it is cyclic. Moreover, as ord
![]() $_{s=1} L(E/ {\mathbb Q} \otimes \chi , s)$
= ord
$_{s=1} L(E/ {\mathbb Q} \otimes \chi , s)$
= ord
![]() $_{s=1} L(E/ {\mathbb Q} \otimes \overline {\chi }, s)$
, we have
$_{s=1} L(E/ {\mathbb Q} \otimes \overline {\chi }, s)$
, we have
![]() $ \chi = \overline {\chi }$
, and so
$ \chi = \overline {\chi }$
, and so
![]() $ [F_1 : {\mathbb Q}]=2$
. Suppose
$ [F_1 : {\mathbb Q}]=2$
. Suppose
![]() $F_1$
is of discriminant D. Since,
$F_1$
is of discriminant D. Since,
![]() $L(E/F_1,s) = L(E/ {\mathbb Q}, s) \cdot L(E_D/{\mathbb Q}, s)$
, we have ord
$L(E/F_1,s) = L(E/ {\mathbb Q}, s) \cdot L(E_D/{\mathbb Q}, s)$
, we have ord
![]() $_{s=1} L(E_D/{\mathbb Q}, s) = 1 $
, and therefore
$_{s=1} L(E_D/{\mathbb Q}, s) = 1 $
, and therefore
![]() ${\mathbf {rk}} E_D({\mathbb Q}) = 1$
. Thus
${\mathbf {rk}} E_D({\mathbb Q}) = 1$
. Thus
![]() ${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E(F_1) = {\mathbf {rk}} E({\mathbb Q}) +1$
.
${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E(F_1) = {\mathbf {rk}} E({\mathbb Q}) +1$
.
Corollary 6.3 If ord
![]() $_{s=1} \; L(E/{\mathbb Q},s) = {\mathbf {rk}} E({\mathbb Q})$
and
$_{s=1} \; L(E/{\mathbb Q},s) = {\mathbf {rk}} E({\mathbb Q})$
and
![]() $K/ {\mathbb Q}$
is a quadratic extension, then
$K/ {\mathbb Q}$
is a quadratic extension, then
The corollary follows from the fact that in this case both of the minimal subfields are equal to K. Also note that it is unconditional, as holomorphy of
![]() $L(E/{\mathbb Q} \otimes \chi , s)$
is known in cyclic case.
$L(E/{\mathbb Q} \otimes \chi , s)$
is known in cyclic case.
The holomorphy condition of
![]() $L(E/ {\mathbb Q} \otimes \chi )$
in Theorem 6.2(ii) can be relaxed if E has complex multiplication. We discuss this next.
$L(E/ {\mathbb Q} \otimes \chi )$
in Theorem 6.2(ii) can be relaxed if E has complex multiplication. We discuss this next.
Let G be a finite group and
![]() $H \leq G$
be any subgroup. For every complex character
$H \leq G$
be any subgroup. For every complex character
![]() $\psi $
of H, we attach a complex number
$\psi $
of H, we attach a complex number
![]() $n(H, \psi )$
satisfying:
$n(H, \psi )$
satisfying:
-
(i)
 $n(H, \psi + \psi ') = n(H, \psi ) + n(H, \psi ')$
, and
$n(H, \psi + \psi ') = n(H, \psi ) + n(H, \psi ')$
, and -
(ii)
 $n(G, $
Ind
$n(G, $
Ind
 $_H^G \psi ) = n(H, \psi )$
.
$_H^G \psi ) = n(H, \psi )$
.
Define
![]() $\theta _H = \sum _{\psi \in \text {Irr}(G)} n(H, \psi ) \psi $
. Then we have,
$\theta _H = \sum _{\psi \in \text {Irr}(G)} n(H, \psi ) \psi $
. Then we have,
![]() $\theta _G|_H = \theta _H$
(see [Reference Murty and Kumar Murty21, Proposition 1, p. 484]). The following is proved in [Reference Murty20, Theorem 14].
$\theta _G|_H = \theta _H$
(see [Reference Murty and Kumar Murty21, Proposition 1, p. 484]). The following is proved in [Reference Murty20, Theorem 14].
Theorem 6.4
(M. Ram Murty) Suppose
![]() $n(H, 1) \geq n(G, 1)$
for every cyclic subgroup H of G. Then
$n(H, 1) \geq n(G, 1)$
for every cyclic subgroup H of G. Then
where “reg” denotes the regular character of G.
We also note the following theorem from [Reference Murty and Kumar Murty21, Theorem 1].
Theorem 6.5
(M. Ram Murty and V. Kumar Murty) Let E be an elliptic curve defined over K. Suppose that E has complex multiplication (CM) and F is a finite extension of K. If F is contained in a solvable extension of K, then
![]() $L(E/F,s) / L(E/K,s)$
is entire.
$L(E/F,s) / L(E/K,s)$
is entire.
Combining the above two theorems, we get the following.
Theorem 6.6 Let
![]() $E/{\mathbb Q}$
be an elliptic curve, and let
$E/{\mathbb Q}$
be an elliptic curve, and let
![]() $K/{\mathbb Q}$
be a solvable Galois extension with Galois group G. Suppose E has complex multiplication. If ord
$K/{\mathbb Q}$
be a solvable Galois extension with Galois group G. Suppose E has complex multiplication. If ord
![]() $_{s=1} \; L(E/K,s) = $
ord
$_{s=1} \; L(E/K,s) = $
ord
![]() $_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
, then
![]() ${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
.
Proof Let
![]() $n(H, \psi )$
= ord
$n(H, \psi )$
= ord
![]() $_{s=1} L(E/K^H \otimes \psi , s)$
. For any cyclic subgroup H of G,
$_{s=1} L(E/K^H \otimes \psi , s)$
. For any cyclic subgroup H of G,
![]() $L(E/K^H \otimes \psi , s)$
is entire, moreover by Theorem 6.5,
$L(E/K^H \otimes \psi , s)$
is entire, moreover by Theorem 6.5,
![]() $L(E/K^H,s)/L(E/{\mathbb Q},s)$
is entire and so conditions of Theorem 6.4 are satisfied. In particular,
$L(E/K^H,s)/L(E/{\mathbb Q},s)$
is entire and so conditions of Theorem 6.4 are satisfied. In particular,
Thus, it must be that, there exists a linear character
![]() $\chi _1$
, such that
$\chi _1$
, such that
![]() $n(G, \chi _1) = 1$
and
$n(G, \chi _1) = 1$
and
![]() $n(G, \chi ) = 0$
for all
$n(G, \chi ) = 0$
for all
![]() $\chi \neq 1, \chi _1$
. That is,
$\chi \neq 1, \chi _1$
. That is,
![]() $L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
$L(E/{\mathbb Q} \otimes \chi , s)$
is holomorphic at
![]() $s=1$
for all irreducible characters
$s=1$
for all irreducible characters
![]() $\chi $
of G. Thus, the condition of Theorem 6.2(ii) is satisfied and we have
$\chi $
of G. Thus, the condition of Theorem 6.2(ii) is satisfied and we have
![]() ${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
if ord
${\mathbf {rk}} E(K) \geq {\mathbf {rk}} E({\mathbb Q}) + 1 $
if ord
![]() $_{s=1} \; L(E/K,s) = $
ord
$_{s=1} \; L(E/K,s) = $
ord
![]() $_{s=1} \; L(E/{\mathbb Q},s) + 1$
.
$_{s=1} \; L(E/{\mathbb Q},s) + 1$
.
Acknowledgments
I would like to thank Prof. V. Kumar Murty for several valuable suggestions and encouragement. I also thank all past and present members of the GANITA Lab for patiently listening to the talks I gave while preparing the draft of this article and for providing their helpful inputs.