Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T17:48:00.365Z Has data issue: false hasContentIssue false
  • English
  • Français

Merge Decompositions, Two-sided Krohn–Rhodes, and Aperiodic Pointlikes

Part of: Theory of computing Semigroups

Published online by Cambridge University Press:  07 January 2019

Samuel J. van Gool  and
Benjamin Steinberg
Samuel J. van Gool
Affiliation:
Department of Mathematics, City College of New York, New York, New York 10031, USA Email: [email protected]@ccny.cuny.edu
Benjamin Steinberg
Affiliation:
Department of Mathematics, City College of New York, New York, New York 10031, USA Email: [email protected]@ccny.cuny.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper provides short proofs of two fundamental theorems of finite semigroup theory whose previous proofs were significantly longer, namely the two-sided Krohn-Rhodes decomposition theorem and Henckell’s aperiodic pointlike theorem. We use a new algebraic technique that we call the merge decomposition. A prototypical application of this technique decomposes a semigroup 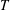$T$ into a two-sided semidirect product whose components are built from two subsemigroups 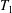$T_{1}$, 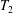$T_{2}$, which together generate 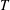$T$, and the subsemigroup generated by their setwise product 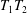$T_{1}T_{2}$. In this sense we decompose 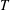$T$ by merging the subsemigroups 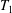$T_{1}$ and 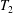$T_{2}$. More generally, our technique merges semigroup homomorphisms from free semigroups.

Keywords

Krohn-Rhodes theoremaperiodic pointlikes

MSC classification

Primary: 20M07: Varieties and pseudovarieties of semigroups
Secondary: 20M35: Semigroups in automata theory, linguistics, etc. 68Q70: Algebraic theory of languages and automata
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 199 - 208
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author S. J. v. G. was supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant #655941. Author B. S. was supported by United States–Israel Binational Science Foundation #2012080 and NSA MSP #H98230-16-1-0047.

References

Almeida, J., Some algorithmic problems for pseudovarieties . Publ. Math. Debrecen 54(1999), no. suppl., 531–552.Google Scholar
Auinger, K. and Steinberg, B., On the extension problem for partial permutations . Proc. Amer. Math. Soc. 131(2003), no. 9, 2693–2703. https://doi.org/10.1090/S0002-9939-03-06860-6.Google Scholar
Eilenberg, S., Automata, languages, and machines. Vol. B. Pure and Applied Mathematics, 59, Academic Press, New York, 1976.Google Scholar
Gool, S. J. v. and Steinberg, B., Pointlike sets for varieties determined by groups. 2018. arxiv:1801.04638.Google Scholar
Henckell, K., Pointlike sets: the finest aperiodic cover of a finite semigroup . J. Pure Appl. Algebra 55(1988), 85–126. https://doi.org/10.1016/0022-4049(88)90042-4.Google Scholar
Henckell, K., Lazarus, S., and Rhodes, J., Prime decomposition theorem for arbitrary semigroups: general holonomy decomposition and synthesis theorem . J. Pure Appl. Algebra 55(1988), no. 1–2, 127–172. https://doi.org/10.1016/0022-4049(88)90043-6.Google Scholar
Henckell, K., Rhodes, J., and Steinberg, B., Aperiodic pointlikes and beyond . Internat. J. Algebra Comput. 20(2010), no. 2, 287–305. https://doi.org/10.1142/S0218196710005662.Google Scholar
Krohn, K. and Rhodes, J., Algebraic theory of machines. I. Prime decomposition theorem for finite semigroups and machines . Trans. Amer. Math. Soc. 116(1965), 450–464. https://doi.org/10.2307/1994127.Google Scholar
Krohn, K., Rhodes, J., and Tilson, B., Algebraic theory of machines, languages, and semigroups. Academic Press, New York, 1968.Google Scholar
Lee, E. W. H., Rhodes, J., and Steinberg, B., Join irreducible semigroups. 2017. arxiv:1702.03753.Google Scholar
Place, T. and Zeitoun, M., Separating regular languages with first-order logic . Log. Methods Comput. Sci. 12(2016), Paper no. 5. https://doi.org/10.2168/LMCS-12(1:5)2016.Google Scholar
Rhodes, J. and Steinberg, B., Pointlike sets, hyperdecidability and the identity problem for finite semigroups . Internat. J. Algebra Comput. 9(1999), no. 3–4, 475–481. https://doi.org/10.1142/S021819679900028X.Google Scholar
Rhodes, J. and Steinberg, B., The q-theory of finite semigroups. Springer Monographs in Mathematics, Springer, New York, 2009.Google Scholar
Steinberg, B., A strange two-variable recursion. MathOverflow question, answered by M. Fischler. https://mathoverflow.net/q/278517.Google Scholar
Steinberg, B., On pointlike sets and joins of pseudovarieties . Internat. J. Algebra Comput. 8(1998), no. 2, 203–234. https://doi.org/10.1142/S0218196798000119.Google Scholar
Straubing, H., Finite automata, formal logic, and circuit complexity. Progress in Theoretical Computer Science, Birkhäuser Boston Inc., Boston, MA, 1994. https://doi.org/10.1007/978-1-4612-0289-9.Google Scholar
Wilke, T., Classifying discrete temporal properties . In: STACS’99, Lecture Notes. in Computer Science, 1563, Springer, 1999, pp. 32–46. https://doi.org/10.1007/3-540-49116-3_3.Google Scholar