Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T10:21:30.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Measures with Fourier Transforms in L2 of a Half-space

Published online by Cambridge University Press:  20 November 2018

Bassam Shayya
Bassam Shayya*
Affiliation:
Department of Mathematics, American University of Beirut, Beirut, Lebanone-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if the Fourier transform of a compactly supported measure is in 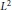${{L}^{2}}$ of a half-space, then the measure is absolutely continuous to Lebesgue measure. We then show how this result can be used to translate information about the dimensionality of a measure and the decay of its Fourier transform into geometric information about its support.

Keywords

42B1028A75
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 172 - 179
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Erdogan, M. B., A bilinear Fourier extension theorem and applications to the distance set problem. Int. Math. Res. Not. 2005, no. 23, 1411–1425.Google Scholar
[2] Forelli, F., Analytic and quasi-invariant measures. Acta Math. 118(1967), 33–59. doi:10.1007/BF02392475Google Scholar
[3] Forelli, F., The theorem of F. and M. Riesz for unbounded measures. In: The Madison symposium on complex analysis (Madison, WI, 1991), Contemp. Math., 137, American Mathematical Society, Providence, RI, 1992, pp. 221–234.Google Scholar
[4] Herz, C. S., Fourier transforms related to convex sets. Ann. of Math. 75(1962), 81–92. doi:10.2307/1970421Google Scholar
[5] Hofmann, S. and Iosevich, A., Circular averages and Falconer/Erdös distance conjecture in the plane for random metrics. Proc. Amer. Math. Soc. 133(2005), no. 1, 133–143. doi:10.1090/S0002-9939-04-07603-8Google Scholar
[6] Mattila, P., Spherical averages of Fourier transforms of measures with finite energy; dimension of intersections and distance sets. Mathematika 34(1987), no. 2, 207–228. doi:10.1112/S0025579300013462Google Scholar
[7] Wolff, T. H., Lectures on harmonic analysis. University Lecture Series, 29, American Mathematical Society, Providence, RI, 2003.Google Scholar