Fix an irreducible (finite) root system $R$ and a choice of positive roots. For any algebraically closed field $k$ consider the almost simple, simply connected algebraic group 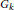${{G}_{k}}$ over $k$ with root system $k$. One associates with any dominant weight $\lambda $ for $R$ two 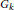${{G}_{k}}$-modules with highest weight $\lambda $, the Weyl module 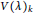$V{{(\lambda )}_{k}}$ and its simple quotient 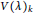$V{{(\lambda )}_{k}}$. Let $\lambda $ and $\mu $ be dominant weights with 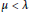$\mu <\lambda $ such that $\mu $ is maximal with this property. Garibaldi, Guralnick, and Nakano have asked under which condition there exists $k$ such that 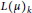$L{{(\mu )}_{k}}$ is a composition factor of 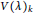$V{{(\lambda )}_{k}}$, and they exhibit an example in type 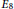${{E}_{8}}$ where this is not the case. The purpose of this paper is to to show that their example is the only one. It contains two proofs for this fact: one that uses a classiffication of the possible pairs 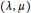$(\lambda ,\mu )$, and another that relies only on the classiûcation of root systems.