Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T16:18:35.020Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal Subbundles of Rank 2 Vector Bundles on Projective Curves

Published online by Cambridge University Press:  20 November 2018

E. Ballico
E. Ballico*
Affiliation:
Department of Mathematics Università di Trento 38050 Povo (TN) Italy, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 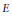$E$ be a stable rank 2 vector bundle on a smooth projective curve 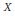$X$ and 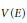$V\,\left( E \right)$ be the set of all rank 1 subbundles of 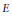$E$ with maximal degree. Here we study the varieties (non-emptyness, irreducibility and dimension) of all rank 2 stable vector bundles, 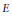$E$, on 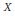$X$ with fixed 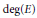$\deg \left( E \right)$ and 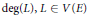$\deg \left( L \right),\,L\,\in \,V\left( E \right)$ and such that 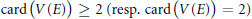$\text{card}\,\left( V(E) \right)\,\ge \,2\,(\text{resp}\text{. card}\left( V(E) \right)\,=\,2)$.

Keywords

14H60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 2 , 01 June 2000 , pp. 129 - 137
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Accola, R. D. M., Topics in the Theory of Riemann Surfaces. Lecture Notes in Math. 1595, Springer-Verlag, 1994.Google Scholar
[2] Arbarello, E. and Cornalba, M., Footnotes to a paper by Beniamino Segre. Math. Ann. 256(1981), 341–362.Google Scholar
[3] Arbarello, E., Cornalba, M., Griffiths, Ph. and Harris, J., Geometry of Algebraic Curves. Vol. I, Grundlehren Math.Wiss. 267, Springer-Verlag, 1985.Google Scholar
[4] Butler, D. C., Families of maximal subbundles of rank two bundles on a curve. Math. Ann. 307(1997), 29–39.Google Scholar
[5] Fulton, W. and Lazarsfeld, R., On the connectedness of degeneracy loci and special divisors. Acta Math. 146(1981), 271–283.Google Scholar
[6] Ghione, F., Quelques résultats de Corrado Segre sur les surfaces réglées. Math. Ann. 255(1981), 77–95.Google Scholar
[7] Gieseker, D., Stable curves and special divisors. Invent.Math. 66(1982), 251–275.Google Scholar
[8] Gunning, R. C., Lectures on Riemann Surfaces: Jacobi varieties. Mathematical Notes 12, Princeton University Press, 1972.Google Scholar
[9] Hirschowitz, A., Rank techniques and jump stratifications. In: Vector bundles on Algebraic Varieties, Proc. Bombay 1984, Oxford University Press, 1987, 159–205.Google Scholar
[10] Lange, H., Higher secant varieties on curves and the theorem of Nagata on ruled surfaces. Manuscripta Math. 47(1984), 263–269.Google Scholar
[11] Lange, H., Höhere Sekantenvarietäten und Vektorbündel auf Kurven. Manuscripta Math. 52(1985), 63–80.Google Scholar
[12] Lange, H. and Narasimhan, M. S., Maximal subbundles of rank two vector bundles on curves. Math. Ann. 266(1983), 55–72.Google Scholar