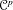Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Binyamini, Gal
and
Novikov, Dmitry
2021.
The Yomdin–Gromov Algebraic Lemma Revisited.
Arnold Mathematical Journal,
Vol. 7,
Issue. 3,
p.
419.
Pawłucki, Wiesław
2024.
Strict $${\mathcal {C}}^p$$-triangulations of sets locally definable in o-minimal structures with an application to a $$\mathcal C^p$$-approximation problem.
Revista Matemática Complutense,
Vol. 37,
Issue. 3,
p.
713.