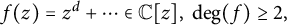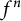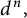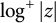1 Main results
For an arbitrary polynomial
![]() $P(z)=c_n\prod _{k=1}^{n}(z-z_k)\in {\mathbb C}[z]$
with
$P(z)=c_n\prod _{k=1}^{n}(z-z_k)\in {\mathbb C}[z]$
with
![]() $c_n\neq 0,$
the Mahler measure is given by
$c_n\neq 0,$
the Mahler measure is given by
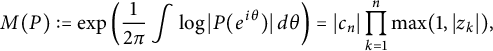 $$ \begin{align} M(P) := \exp\left(\frac{1}{2\pi}\int \log|P(e^{i\theta})|\,d\theta\right) = |c_n| \prod_{k=1}^{n} \max(1,|z_k|), \end{align} $$
$$ \begin{align} M(P) := \exp\left(\frac{1}{2\pi}\int \log|P(e^{i\theta})|\,d\theta\right) = |c_n| \prod_{k=1}^{n} \max(1,|z_k|), \end{align} $$
where the second equality is a well-known consequence of Jensen’s formula (see [Reference Borwein2, Reference Everest and Ward7, Reference McKee and Smyth11] for background and applications).
Let
![]() $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
and consider the n-fold iterates for f denoted by
$f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
and consider the n-fold iterates for f denoted by
![]() $f^n$
, which are monic polynomials of degree
$f^n$
, which are monic polynomials of degree
![]() $d^n,\ n\in {\mathbb N}.$
At a recent conference [Reference Granville9], Granville asked interesting questions on the behavior of the Mahler measure under composition of polynomials. In particular, how the Mahler measure of the polynomial iterates
$d^n,\ n\in {\mathbb N}.$
At a recent conference [Reference Granville9], Granville asked interesting questions on the behavior of the Mahler measure under composition of polynomials. In particular, how the Mahler measure of the polynomial iterates
![]() $f^n$
behaves as
$f^n$
behaves as
![]() $n\to \infty .$
Our primary goal is to show that the Mahler measure of
$n\to \infty .$
Our primary goal is to show that the Mahler measure of
![]() $f^n$
grows geometrically fast with the degree
$f^n$
grows geometrically fast with the degree
![]() $d^n$
. In order to state a precise result, we need to introduce the Julia set of f denoted by J, which is a completely invariant compact set under iteration of f (see, e.g., [Reference Carleson and Gamelin4] for details). It is also known that there is a unique unit Borel measure
$d^n$
. In order to state a precise result, we need to introduce the Julia set of f denoted by J, which is a completely invariant compact set under iteration of f (see, e.g., [Reference Carleson and Gamelin4] for details). It is also known that there is a unique unit Borel measure
![]() $\mu _J$
supported on J that is invariant under f. In fact,
$\mu _J$
supported on J that is invariant under f. In fact,
![]() $\mu _J$
is the equilibrium measure of J in the sense of logarithmic potential theory (see [Reference Carleson and Gamelin4, Reference Ransford13]), and it expresses the steady-state distribution of charge if J is viewed as conductor.
$\mu _J$
is the equilibrium measure of J in the sense of logarithmic potential theory (see [Reference Carleson and Gamelin4, Reference Ransford13]), and it expresses the steady-state distribution of charge if J is viewed as conductor.
Theorem 1.1 If
![]() $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is different from the monomial
$f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is different from the monomial
![]() $z^d$
, then we have
$z^d$
, then we have
where
![]() $\mu _J$
is the invariant (equilibrium) measure of the Julia set J for f.
$\mu _J$
is the invariant (equilibrium) measure of the Julia set J for f.
Remark 1.2 If
![]() $f(z)=z^d$
, then
$f(z)=z^d$
, then
![]() $f^n(z)=z^{d^n},\ n\in {\mathbb N},$
and
$f^n(z)=z^{d^n},\ n\in {\mathbb N},$
and
![]() $M(f^n) = 1,\ n\in {\mathbb N},$
by (1.1). Also note that the smallest value of
$M(f^n) = 1,\ n\in {\mathbb N},$
by (1.1). Also note that the smallest value of
![]() $\int \log ^+|z| d\mu _J(z)$
is 0 that is attained for
$\int \log ^+|z| d\mu _J(z)$
is 0 that is attained for
![]() $f(z)=z^d$
with
$f(z)=z^d$
with
![]() $J={\mathbb T}:=\{|z|=1\}$
and
$J={\mathbb T}:=\{|z|=1\}$
and
![]() $d\mu _{\mathbb T}(e^{it})=dt/(2\pi ),\ t\in [0,2\pi ).$
$d\mu _{\mathbb T}(e^{it})=dt/(2\pi ),\ t\in [0,2\pi ).$
In light of (1.2), we arrive at the question: How large can
![]() $\int \log ^+|z| d\mu _J(z)$
be? Since the location of the Julia set J varies with f in such a way that J can be essentially anywhere in the complex plane, the value of this integral can be arbitrarily large with the values of
$\int \log ^+|z| d\mu _J(z)$
be? Since the location of the Julia set J varies with f in such a way that J can be essentially anywhere in the complex plane, the value of this integral can be arbitrarily large with the values of
![]() $\log ^+|z|.$
Indeed, if
$\log ^+|z|.$
Indeed, if
![]() $J\subset \{z:|z|>R\}$
, then
$J\subset \{z:|z|>R\}$
, then
![]() $\int \log ^+|z| d\mu _J(z) \ge \log {R}$
because
$\int \log ^+|z| d\mu _J(z) \ge \log {R}$
because
![]() $\mu _J$
is the unit measure, where
$\mu _J$
is the unit measure, where
![]() $R>1$
can be arbitrarily large. However, if we make proper normalization assumptions, then we obtain some precise upper bounds stated below.
$R>1$
can be arbitrarily large. However, if we make proper normalization assumptions, then we obtain some precise upper bounds stated below.
Let K be the filled-in Julia set that consists of the Julia set J and the union of the bounded components of its complement
![]() ${\mathbb C}\,{\backslash}\, J$
(see [Reference Carleson and Gamelin4, p. 65]). It is clear that
${\mathbb C}\,{\backslash}\, J$
(see [Reference Carleson and Gamelin4, p. 65]). It is clear that
![]() $J=\partial K$
, so that K is connected if and only if J is connected, which is known to hold if and only if all the critical points of f are contained in K (see [Reference Carleson and Gamelin4, p. 66]). Moreover, J and K share the same equilibrium measure
$J=\partial K$
, so that K is connected if and only if J is connected, which is known to hold if and only if all the critical points of f are contained in K (see [Reference Carleson and Gamelin4, p. 66]). Moreover, J and K share the same equilibrium measure
![]() $\mu _J=\mu _K$
(cf. [Reference Brolin3, Reference Ransford13]).
$\mu _J=\mu _K$
(cf. [Reference Brolin3, Reference Ransford13]).
Theorem 1.3 If
![]() $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2$
, J is connected, and
$f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2$
, J is connected, and
![]() $0\in K$
, then
$0\in K$
, then
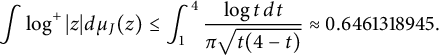 $$ \begin{align} \int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi \sqrt{t(4-t)}} \approx 0.6461318945. \end{align} $$
$$ \begin{align} \int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi \sqrt{t(4-t)}} \approx 0.6461318945. \end{align} $$
Equality holds above for
![]() $J=K=[0,4]$
and
$J=K=[0,4]$
and
![]() $f(z)=2\, T_d(z/2-1)$
, where
$f(z)=2\, T_d(z/2-1)$
, where
![]() $T_d(z)=\cos (d\arccos {z})$
is the classical Chebyshev polynomial.
$T_d(z)=\cos (d\arccos {z})$
is the classical Chebyshev polynomial.
Symmetry assumptions also produce interesting results such as the one below.
Theorem 1.4 If
![]() $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is either an odd or an even function, and J is connected, then
$f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is either an odd or an even function, and J is connected, then
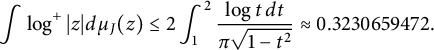 $$ \begin{align} \int \log^+|z| d\mu_J(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi \sqrt{1-t^2}} \approx 0.3230659472. \end{align} $$
$$ \begin{align} \int \log^+|z| d\mu_J(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi \sqrt{1-t^2}} \approx 0.3230659472. \end{align} $$
Equality holds above for
![]() $J=[-2,2]$
and
$J=[-2,2]$
and
![]() $f(z)=2\, T_d(z/2)$
, where
$f(z)=2\, T_d(z/2)$
, where
![]() $T_d(z)=\cos (d\arccos {z})$
.
$T_d(z)=\cos (d\arccos {z})$
.
A classical example that satisfies the assumptions of Theorem 1.4 is given by the family of quadratic polynomials
![]() $f(z)=z^2+c$
with c from the Mandelbrot set (see Chapter VIII of [Reference Carleson and Gamelin4]).
$f(z)=z^2+c$
with c from the Mandelbrot set (see Chapter VIII of [Reference Carleson and Gamelin4]).
We remark that the growth of the Mahler measure for the iterates exhibited here is essentially due to the intrinsic connection of the Mahler measure to the unit circle. A more suitable version of the Mahler measure for the dynamical setting is known (see the recent papers [Reference Carter, Lalín, Manes and Miller5, Reference Carter, Lalín, Manes, Miller and Mocz6], where the first one surveys many developments in the area). Another related notion is dynamical (or canonical) height (see [Reference Silverman14] for a comprehensive exposition). There are many other connections of the Mahler measure and its generalizations with polynomial dynamics. Thus, the integral of (1.2) can be interpreted as the Arakelov–Zhang pairing of f and
![]() $z^2$
that arises as a limit of average Weil heights in [Reference Petsche, Szpiro and Tucker12]. It is practically impossible to discuss all these interesting relations in detail in this short note.
$z^2$
that arises as a limit of average Weil heights in [Reference Petsche, Szpiro and Tucker12]. It is practically impossible to discuss all these interesting relations in detail in this short note.
For the proofs of Theorems 1.1, 1.3, and 1.4, we need the well-known result of Brolin [Reference Brolin3, Theorem 16.1] on the equidistribution of preimages for the iterates
![]() $f^n$
:
$f^n$
:
Brolin’s Theorem. Let
![]() $w\in {\mathbb C}$
be any point with one possible exception. Consider the preimages of w under
$w\in {\mathbb C}$
be any point with one possible exception. Consider the preimages of w under
![]() $f^n$
denoted by
$f^n$
denoted by
![]() $\{z_{k,n}\}_{k=1}^{d^n},$
i.e., all solutions of the equation
$\{z_{k,n}\}_{k=1}^{d^n},$
i.e., all solutions of the equation
![]() $f^n(z)=w$
listed according to multiplicities. Define the normalized counting measures in those preimages by
$f^n(z)=w$
listed according to multiplicities. Define the normalized counting measures in those preimages by
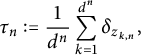 $$ \begin{align} \tau_n := \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}}, \end{align} $$
$$ \begin{align} \tau_n := \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}}, \end{align} $$
where
![]() $\delta _z$
denotes a unit point mass at
$\delta _z$
denotes a unit point mass at
![]() $z.$
Then we have the following weak* convergence:
$z.$
Then we have the following weak* convergence:
Brolin’s result has the following implication, which is crucial for our purposes.
Corollary 1.5. If
![]() $f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is not the monomial
$f(z)=z^d+\cdots \in {\mathbb C}[z],\ \deg (f)\ge 2,$
is not the monomial
![]() $z^d$
, then we have for the zeros of
$z^d$
, then we have for the zeros of
![]() $f^n$
denoted by
$f^n$
denoted by
![]() $\{z_{k,n}\}_{k=1}^{d^n}$
that
$\{z_{k,n}\}_{k=1}^{d^n}$
that
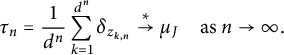 $$ \begin{align} \tau_n = \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}} \stackrel{*}{\rightarrow} \mu_J \quad\mbox{as }n\to\infty. \end{align} $$
$$ \begin{align} \tau_n = \frac{1}{d^n} \sum_{k=1}^{d^n} \delta_{z_{k,n}} \stackrel{*}{\rightarrow} \mu_J \quad\mbox{as }n\to\infty. \end{align} $$
Proof The exceptional points in Brolin’s Theorem arise as values omitted by the family of iterates
![]() $\{f^n\}_{n=1}^\infty $
in a neighborhood of any point
$\{f^n\}_{n=1}^\infty $
in a neighborhood of any point
![]() $\zeta \in J$
. It follows that there are at most two such omitted values by Montel’s theorem on normal families, for otherwise the family
$\zeta \in J$
. It follows that there are at most two such omitted values by Montel’s theorem on normal families, for otherwise the family
![]() $\{f^n\}_{n=1}^\infty $
would be normal in that neighborhood, which contradicts the definition of the Julia set J for f. Moreover, Lemma 2.2 of [Reference Brolin3] states that the exceptional values are the same for all points
$\{f^n\}_{n=1}^\infty $
would be normal in that neighborhood, which contradicts the definition of the Julia set J for f. Moreover, Lemma 2.2 of [Reference Brolin3] states that the exceptional values are the same for all points
![]() $\zeta \in J.$
Since f is a polynomial in our settings, it certainly omits the value
$\zeta \in J.$
Since f is a polynomial in our settings, it certainly omits the value
![]() $\infty $
in every disk
$\infty $
in every disk
![]() $\{z:|z-\zeta |<r\},$
where
$\{z:|z-\zeta |<r\},$
where
![]() $r>0,\ \zeta \in J,$
so that at most one exceptional value can occur in this case. For example, if
$r>0,\ \zeta \in J,$
so that at most one exceptional value can occur in this case. For example, if
![]() $f(z)=z^d$
, then this exceptional value is
$f(z)=z^d$
, then this exceptional value is
![]() $0$
in every disk
$0$
in every disk
![]() $\{z:|z-\zeta |<1\},$
where
$\{z:|z-\zeta |<1\},$
where
![]() $\zeta \in J={\mathbb T}$
the unit circumference. However,
$\zeta \in J={\mathbb T}$
the unit circumference. However,
![]() $0$
cannot be an exceptional value for any polynomial in Theorem 1.1. Indeed, since
$0$
cannot be an exceptional value for any polynomial in Theorem 1.1. Indeed, since
![]() $\deg (f)\ge 2$
and f is not the monomial
$\deg (f)\ge 2$
and f is not the monomial
![]() $z^d,$
there is a root
$z^d,$
there is a root
![]() $w_0\neq 0$
of f. If we assume that
$w_0\neq 0$
of f. If we assume that
![]() $0$
is an exceptional point for Brolin’s Theorem, equivalently an omitted value for the family
$0$
is an exceptional point for Brolin’s Theorem, equivalently an omitted value for the family
![]() $\{f^n\}_{n=1}^\infty $
in a neighborhood V of a point
$\{f^n\}_{n=1}^\infty $
in a neighborhood V of a point
![]() $\zeta \in J,$
then the same must be true for
$\zeta \in J,$
then the same must be true for
![]() $w_0$
because
$w_0$
because
![]() $f^n(z_0)=w_0$
for a point
$f^n(z_0)=w_0$
for a point
![]() $z_0\in V$
implies
$z_0\in V$
implies
![]() $f^{n+1}(z_0)=0$
. But two finite omitted values
$f^{n+1}(z_0)=0$
. But two finite omitted values
![]() $0,w_0$
mean that the family
$0,w_0$
mean that the family
![]() $\{f^n\}_{n=1}^\infty $
must be normal in V, contradicting the definition of the Julia set
$\{f^n\}_{n=1}^\infty $
must be normal in V, contradicting the definition of the Julia set
![]() $J.$
Thus,
$J.$
Thus,
![]() $0$
is not an exceptional point, and Corollary 1.5 is an immediate consequence of Brolin’s Theorem.
$0$
is not an exceptional point, and Corollary 1.5 is an immediate consequence of Brolin’s Theorem.
2 Proofs of the main results
We continue with the same notations as before.
Proof of Theorem 1.1
It is clear from (1.1) that
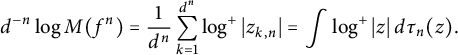 $$\begin{align*}d^{-n} \log M(f^n) = \frac{1}{d^n} \sum_{k=1}^{d^n} \log^+|z_{k,n}| = \int \log^+|z|\,d\tau_n(z). \end{align*}$$
$$\begin{align*}d^{-n} \log M(f^n) = \frac{1}{d^n} \sum_{k=1}^{d^n} \log^+|z_{k,n}| = \int \log^+|z|\,d\tau_n(z). \end{align*}$$
Since
![]() $\log ^+|z|$
is a continuous function in
$\log ^+|z|$
is a continuous function in
![]() ${\mathbb C}$
, the limit relation in (1.2) follows from the weak* convergence of (1.7). One only needs to observe here that the sets
${\mathbb C}$
, the limit relation in (1.2) follows from the weak* convergence of (1.7). One only needs to observe here that the sets
![]() $\{z_{k,n}\}_{k=1}^{d^n}$
are uniformly bounded for all
$\{z_{k,n}\}_{k=1}^{d^n}$
are uniformly bounded for all
![]() $n\in {\mathbb N},$
say belong to a fixed disk
$n\in {\mathbb N},$
say belong to a fixed disk
![]() $D_R=\{z:|z|\le R\},$
so that
$D_R=\{z:|z|\le R\},$
so that
![]() $\log ^+|z|$
can be extended from
$\log ^+|z|$
can be extended from
![]() $D_R$
to
$D_R$
to
![]() ${\mathbb C}\,{\backslash}\, D_R$
as a continuous function with compact support in
${\mathbb C}\,{\backslash}\, D_R$
as a continuous function with compact support in
![]() ${\mathbb C}.$
${\mathbb C}.$
The inequality in (1.2) follows from the work of Fernández [Reference Fernández8], who showed that the Julia set J of f different from
![]() $z^d$
must have points in the domain
$z^d$
must have points in the domain
![]() $\Delta =\{z:|z|>1\}.$
It is well known that supp
$\Delta =\{z:|z|>1\}.$
It is well known that supp
![]() $\,\mu _J = J$
(see [Reference Brolin3, Lemma 15.2] and [Reference Ransford13, pp. 195–197]). Thus,
$\,\mu _J = J$
(see [Reference Brolin3, Lemma 15.2] and [Reference Ransford13, pp. 195–197]). Thus,
Proof of Theorem 1.3
Recall that the logarithmic capacity of the Julia set for a monic polynomial is equal to 1 (see Lemma 15.1 of [Reference Brolin3] and Theorem 6.5.1 of [Reference Ransford13] for a detailed proof). The book [Reference Ransford13] contains a complete account on logarithmic potential theory, and on capacity in particular. Since
![]() $J=\partial K$
, the equilibrium measure of K is
$J=\partial K$
, the equilibrium measure of K is
![]() $\mu _K=\mu _J$
, and the capacity of K is 1 (cf. [Reference Ransford13]). Clearly, K is a connected set because J is so. The conditions that the capacity of K is 1,
$\mu _K=\mu _J$
, and the capacity of K is 1 (cf. [Reference Ransford13]). Clearly, K is a connected set because J is so. The conditions that the capacity of K is 1,
![]() $0\in K$
and K is connected introduce restrictions on the size of K and, consequently, on the size of the integral
$0\in K$
and K is connected introduce restrictions on the size of K and, consequently, on the size of the integral
![]() $\int \log ^+|z| d\mu _J(z)$
in (1.2). Theorem 6.2 of [Reference Baernstein, Laugesen and Pritsker1] (see also Corollary 6 of [Reference Laugesen10]) gives that the largest value of this integral is attained when
$\int \log ^+|z| d\mu _J(z)$
in (1.2). Theorem 6.2 of [Reference Baernstein, Laugesen and Pritsker1] (see also Corollary 6 of [Reference Laugesen10]) gives that the largest value of this integral is attained when
![]() $K=[0,4]=J$
, in which case it is well known [Reference Ransford13] that
$K=[0,4]=J$
, in which case it is well known [Reference Ransford13] that
 $$\begin{align*}d\mu_K(x) = d\mu_J(x) = \frac{dx}{\pi\sqrt{x(4-x)}}, \quad x\in(0,4). \end{align*}$$
$$\begin{align*}d\mu_K(x) = d\mu_J(x) = \frac{dx}{\pi\sqrt{x(4-x)}}, \quad x\in(0,4). \end{align*}$$
To apply Theorem 6.2 of [Reference Baernstein, Laugesen and Pritsker1], we also need to note that
![]() $\log ^+|z| = \max (0,\log |z|)$
is clearly a convex function of
$\log ^+|z| = \max (0,\log |z|)$
is clearly a convex function of
![]() $\log |z|.$
Thus, we have the upper bound (1.3)
$\log |z|.$
Thus, we have the upper bound (1.3)
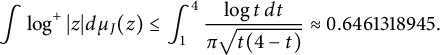 $$\begin{align*}\int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi\sqrt{t(4-t)}} \approx 0.6461318945. \end{align*}$$
$$\begin{align*}\int \log^+|z| d\mu_J(z) \le \int_{1}^{4}\frac{\log{t}\,dt}{\pi\sqrt{t(4-t)}} \approx 0.6461318945. \end{align*}$$
The case of equality for
![]() $J=[0,4]$
is attained by the polynomial
$J=[0,4]$
is attained by the polynomial
![]() $f(z)=2\, T_d(z/2-1)$
, where
$f(z)=2\, T_d(z/2-1)$
, where
![]() $T_d(z)=\cos (d\arccos {z})$
is the classical Chebyshev polynomial of the first kind (see Sections 1.6.2 and 6.2 of [Reference Silverman14] for details).
$T_d(z)=\cos (d\arccos {z})$
is the classical Chebyshev polynomial of the first kind (see Sections 1.6.2 and 6.2 of [Reference Silverman14] for details).
Proof of Theorem 1.4
We proceed with a proof similar to the previous one, but use Corollary 6.3 of [Reference Baernstein, Laugesen and Pritsker1] instead of Theorem 6.2 of [Reference Baernstein, Laugesen and Pritsker1]. We have that capacity of J is 1 by Theorem 6.5.1 of [Reference Ransford13], and J is connected by our assumption. Corollary 6.3 of [Reference Baernstein, Laugesen and Pritsker1] is applied to the filled-in Julia set K, so that
![]() $J=\partial K$
, where the equilibrium measure of K is
$J=\partial K$
, where the equilibrium measure of K is
![]() $\mu _K=\mu _J$
, and the capacity of K is 1. Again, K is connected because J is so. Moreover, both J and K are symmetric with respect to the origin because f is even or odd. If f is odd, then 0 is a fixed point of f, implying that
$\mu _K=\mu _J$
, and the capacity of K is 1. Again, K is connected because J is so. Moreover, both J and K are symmetric with respect to the origin because f is even or odd. If f is odd, then 0 is a fixed point of f, implying that
![]() $0\in K.$
If f is even, then 0 is a critical point of f; hence,
$0\in K.$
If f is even, then 0 is a critical point of f; hence,
![]() $0\in K$
because we assume that J is connected (cf. [Reference Carleson and Gamelin4, p. 66]). Thus,
$0\in K$
because we assume that J is connected (cf. [Reference Carleson and Gamelin4, p. 66]). Thus,
![]() $0\in K$
under our assumptions, and we obtain from Corollary 6.3 of [Reference Baernstein, Laugesen and Pritsker1] that the largest value of the integral in (1.4) is attained for
$0\in K$
under our assumptions, and we obtain from Corollary 6.3 of [Reference Baernstein, Laugesen and Pritsker1] that the largest value of the integral in (1.4) is attained for
![]() $J=K=[-2,2] :$
$J=K=[-2,2] :$
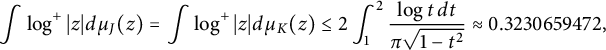 $$\begin{align*}\int \log^+|z| d\mu_J(z) = \int \log^+|z| d\mu_K(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi\sqrt{1-t^2}} \approx 0.3230659472, \end{align*}$$
$$\begin{align*}\int \log^+|z| d\mu_J(z) = \int \log^+|z| d\mu_K(z) \le 2 \int_{1}^{2}\frac{\log{t}\,dt}{\pi\sqrt{1-t^2}} \approx 0.3230659472, \end{align*}$$
where we used that the equilibrium measure for
![]() $J=K=[-2,2]$
is the Chebyshev distribution [Reference Ransford13]
$J=K=[-2,2]$
is the Chebyshev distribution [Reference Ransford13]
It is well known that
![]() $J=[-2,2]$
for
$J=[-2,2]$
for
![]() $f(z)=2\, T_d(z/2)$
, where
$f(z)=2\, T_d(z/2)$
, where
![]() $T_d(z)=\cos (d\arccos {z})$
(see Sections 1.6.2 and 6.2 of [Reference Silverman14]).
$T_d(z)=\cos (d\arccos {z})$
(see Sections 1.6.2 and 6.2 of [Reference Silverman14]).
Acknowledgment
This paper was initiated at the conference “Equidistribution and Arithmetic Dynamics” held at Oklahoma State University during June 20–24, 2022.