Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T17:37:10.635Z Has data issue: false hasContentIssue false
  • English
  • Français

LS-catégorie algébrique et attachement de cellules

Published online by Cambridge University Press:  20 November 2018

Thomas Kahl
Thomas Kahl*
Affiliation:
UMR CNRS 8524 U.F.R. de Mathématiques Université des Sciences et Technologies de Lille 59655 Villeneuve d’Ascq Cedex France, courriel: [email protected]
Rights & Permissions [Opens in a new window]

Résumé

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Nous montrons que la 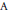$\text{A}$-catégorie d’un espace simplement connexe de type fini est inférieure ou égale à 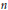$n$ si et seulement si son modèle d’Adams-Hilton est un rétracte homotopique d’une algèbre différentielle à 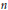$n$ étages. Nous en déduisons que l’invariant Acat augmente au plus de 1 lors de l’attachement d’une cellule à un espace.

Abstract

Abstract

We show that the 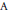$\text{A}$-category of a simply connected space of finite type is less than or equal to 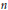$n$ if and only if its Adams-Hilton model is a homotopy retract of an 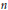$n$-stage differential algebra. We deduce from this that the invariant Acat increases by at most 1 when a cell is attached to a space.

Keywords

55M3018G55LS-categorystrong categoryAdams-Hilton modelscell attachments
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 4 , 01 December 2001 , pp. 459 - 468
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Adams, J. F. and Hilton, P. J., On the chain algebra of a loop space. Comment.Math. Helv. 30 (1955), 305–330.Google Scholar
[2] Baues, H. J., Algebraic Homotopy. Cambridge Univ. Press, Cambridge, 1989.Google Scholar
[3] Cornea, O., Strong LS category equals Cone-length. Topology (2) 34 (1995), 377–381.Google Scholar
[4] Félix, Y., Halperin, S. et Thomas, J.-C., Adams’ cobar equivalence. Trans. Amer.Math. Soc. 329 (1992), 531–549.Google Scholar
[5] Félix, Y., Halperin, S. et Thomas, J.-C., Differential graded algebras in topology. Handbook of Algebraic Topology (ed. I. M. James), North-Holland, 1995.Google Scholar
[6] Ganea, T., Lusternik-Schnirelmann category and strong category. Illinois J. Math. 11 (1967), 417–427.Google Scholar
[7] Halperin, S. et Lemaire, J.-M., Notions of category in differential algebra. Algebraic Topology—Rational Homotopy, Lecture Notes in Math. 1318, Springer-Verlag, 1988, 138–154.Google Scholar
[8] Lemaire, J.-M. et Sigrist, F., Sur les invariants d’homotopie rationnelle liés à la L.S. catégorie. Comment.Math. Helv. 56 (1981), 103–122.Google Scholar
[9] Munkholm, H., DGA algebras as a Quillen model category. J. Pure Appl. Alg. 13 (1978), 221–232.Google Scholar
[10] Quillen, D., Homotopical Algebra. Lecture Notes in Math. 43, Springer-Verlag, 1967.Google Scholar
[11] Scheerer, H. et Tanré, D., Lusternik-Schnirelmann category and algebraic R-local homotopy theory. Canad. J. Math. (4) 50 (1998), 845–862.Google Scholar
[12] Toomer, G. H., Lusternik-Schnirelmann category and the Moore spectral sequence. Math. Z. 138 (1974), pp. 123–143.Google Scholar