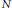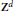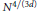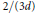Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nachmias, Asaf
and
Peres, Yuval
2012.
Non-amenable Cayley graphs of high girth have $p_c < p_u$ and
mean-field exponents.
Electronic Communications in Probability,
Vol. 17,
Issue. none,
Duminil-Copin, Hugo
Glazman, Alexander
Hammond, Alan
and
Manolescu, Ioan
2016.
On the probability that self-avoiding walk ends at a given point.
The Annals of Probability,
Vol. 44,
Issue. 2,
Bauerschmidt, Roland
Brydges, David C.
and
Slade, Gordon
2019.
Introduction to a Renormalisation Group Method.
Vol. 2242,
Issue. ,
p.
183.
Slade, Gordon
2019.
Self-avoiding walk, spin systems and renormalization.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 475,
Issue. 2221,
p.
20180549.
Hammond, Alan
2019.
On self-avoiding polygons and walks: The snake method via pattern fluctuation.
Transactions of the American Mathematical Society,
Vol. 372,
Issue. 4,
p.
2335.
Guttmann, Anthony J
and
Jensen, Iwan
2022.
On the existence of critical exponents for self-avoiding walks.
Journal of Physics A: Mathematical and Theoretical,
Vol. 55,
Issue. 41,
p.
415206.
Hairer, Martin
2023.
A stroll around the critical Potts model.
Bulletin of the American Mathematical Society,
Chen, Le
Kuzgun, Sefika
Mueller, Carl
and
Xia, Panqiu
2024.
On the Radius of Self-Repellent Fractional Brownian Motion.
Journal of Statistical Physics,
Vol. 191,
Issue. 2,