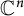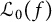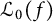1 Introduction
Let
$f (z) = f (z_1, \ldots , z_n) \in \mathbb {C} \{z_1, \ldots , z_n \} = : \mathcal {O}_n$
be a convergent power series defining an isolated singularity at the origin
$0 \in \mathbb {C}^n$
, i.e.,
$f (0) = 0$
and the gradient of f,
$$\begin{align*}\nabla f := \left( \frac{\partial f}{\partial z_1}, \ldots, \frac{\partial f}{\partial z_n} \right) : (\mathbb{C}^n, 0) \rightarrow (\mathbb{C}^n, 0), \end{align*}$$
has an isolated zero at
$0 \in \mathbb {C}^n$
. The Łojasiewicz exponent
$\mathcal {L}_0 (f)$
of f is the smallest
$\theta> 0$
such that there exists a neighborhood U of
$0 \in \mathbb {C}^n$
and a constant
$C> 0$
such that
$$\begin{align*}| \nabla f (z) | \geqslant C | z |^{\theta} \text{ for } z \in U. \end{align*}$$
Remark. One can similarly define the Łojasiewicz exponent
$\mathcal {L}_0 (F)$
of any holomorphic mapping
$F : (\mathbb {C}^n, 0) \rightarrow (\mathbb {C}^p, 0)$
having an isolated zero at
$0 \in \mathbb {C}^n$
.
It is known
$\mathcal {L}_0 (f)$
is a rational positive number, it is an analytic invariant of f, it depends only on the ideal
$(\frac {\partial f}{\partial z_1}, \ldots , \frac {\partial f}{\partial z_n})$
in
$\mathcal {O}_n$
,
$[\mathcal {L}_0 (f)] + 1$
is the degree of
$C^0$
-sufficiency of f and it can be calculated by means of analytic paths, i.e.,
$$ \begin{align} \mathcal{L}_0 (f) = \sup_{\Phi} \frac{\operatorname{ord} (\nabla f \circ \Phi)}{\operatorname{ord} \Phi}, \end{align} $$
where
$0 \neq \Phi = (\varphi _1, \ldots , \varphi _n) \in \mathbb {C} \{t\}^n$
,
$\Phi (0) = 0$
, and
$\operatorname {ord} \Phi := \min _i \operatorname {ord} \varphi _i$
. It is an open and difficult problem if the Łojasiewicz exponent is a topological invariant. There are many explicit formulas and estimations for
$\mathcal {L}_0 (f)$
in various terms and in special classes of singularities (see [Reference Brzostowski, Krasiński and OleksikBrz15, Reference KouchnirenkoKL77, Reference Krasiński, Oleksik and PłoskiKOP09, Reference LichtinLT08, Reference TeissierTei77]).
In the paper, we investigate the problem of determining the Łojasiewicz exponent for nondegenerate (in the Kushnirenko sense) singularities in terms of their Newton polyhedron. This is an answer to V. Arnold’s problem who postulated, “every interesting discrete invariant of a generic singularity with Newton polyhedron
$\Gamma $
is an interesting function of the polyhedron” (Problem 1975–1, see also 1968–2, 1975–21 in [Reference ArnoldArn04]). The most famous example of such an invariant is the Milnor number, which can be calculated using the Kushnirenko formula in the case of nondegenerate singularities (see [Reference Kuo and LuKou76]). Here, we completely solve the above Arnold’s problem for the Łojasiewicz exponent in the class of nondegenerate surface singularities, i.e., for
$n = 3$
. The case
$n = 2$
was solved by Lenarcik in [Reference Lejeune-Jalabert and TeissierLen98]. Other attempts to read off the Łojasiewicz exponent from the Newton polyhedron of a singularity were made by many authors (e.g., Lichtin [Reference LenarcikLic81], Fukui [Reference FukuiFuk91], Bivià-Ausina [Reference Bivià-AusinaBiv03], Abderrahmane [Reference AbderrahmaneAbd05], and Mondal (private communication)). In particular, see the recent paper by Oka [Reference OkaOka18], who, in the n-dimensional case, obtained estimations from above under additional assumptions.
Our formula is that
$\mathcal {L}_0 (f)$
is the maximum of intersections of some explicitly indicated two-dimensional faces of the Newton polyhedron
$\Gamma (f)$
of f with the coordinate axes (we refer to these as proximity faces; see Definition 5.1). The main issue is to find an analytic path
$\Phi $
on which
$\frac {\operatorname {ord} (\nabla f \circ \Phi )}{\operatorname {ord} \Phi }$
is equal to this maximum. It is clear that such a path should be somehow related to the proximity face which realizes the maximum of intersections. Ideally, we would want a path whose order vector is perpendicular to this face and annihilates all the partial derivatives of f except for one. As much as it is simple to find such a path in the two-dimensional case (i.e., for plane curve singularities), doing the same in the three-dimensional case is extremely complicated and, indeed, not always possible. A major part of the proof is devoted to the construction of this type of path whenever it is possible to find one. For this, we need the methods of the combinatorial theory of systems of equations: the classical Bernstein theorem on the number of isolated solutions of a system of polynomial equations (Theorem 3.3), and the Maurer theorem being a generalization of the classical Puiseux theorem (Theorem 3.4). We also need an algebraic result which roughly states that if the weighted initial parts of two formal series
$F,G \in \mathbb {C} [[z_1,\ldots ,z_n]]$
do not generate a monomial, then the ideal
$(F,G)$
does not contain an element whose weighted initial part is a monomial (see Lemma 4.3 for details). In the remaining cases, in which it is impossible to find the analytic path mentioned above, we utilize the special geometric features of proximity faces to indicate another path, one which still is in a close connection with the optimal proximity face and annihilates two of the three partial derivatives of f (Theorem 6.1).
As an application, we have obtained ([Reference BrzostowskiBKO21]) the constancy of the Łojasiewicz exponents in nondegenerate
$\mu $
-constant families of surface singularities.
2 The main theorem
Let
$0 \neq f : (\mathbb {C}^n, 0) \rightarrow (\mathbb {C}, 0)$
be a holomorphic function defined by a convergent power series
$\sum _{\nu \in \mathbb {N}^n} a_{\nu } z^{\nu }$
,
$z = (z_1, \ldots , z_n)$
. Let
$\mathbb {R}_+^n := \{(x_1, \ldots , x_n) \in \mathbb {R}^n : x_i \geqslant 0, i = 1, \ldots , n\}$
. We define
$\operatorname {supp} f := \{\nu \in \mathbb {N}^n : a_{\nu } \neq 0\} \subset \mathbb {R}_+^n$
. In the sequel, we will identify
$\nu = (\nu _1, \ldots , \nu _n) \in \operatorname {supp} f$
with their associated monomials
$z^{\nu } = z_1^{\nu _1} \ldots z_n^{\nu _n}$
. In particular, we will apply the geometric language of the space
$\mathbb {R}_+^n$
to polynomials, e.g., we may say
$z {}^{\nu } \in \operatorname {supp} f$
or that two binomials are parallel (the latter means segments in
$\mathbb {R}_+^n$
associated with these binomials are parallel). We define the Newton polyhedron
$\Gamma _+ (f) \subset \mathbb {R}_+^n$
of f as the convex hull of
$\{\nu +\mathbb {R}_+^n : \nu \in \operatorname {supp} f\}$
. We say f is convenient if
$\Gamma _+ (f)$
has a non-empty intersection with each coordinate axis
$0 x_i \ (i = 1, \ldots , n)$
, and nearly convenient if, for each
$i = 1, \ldots , n$
, in
$\operatorname {supp} f$
there is a monomial of the form
$z_i^m$
or
$z_i^m z_j$
with
$i \neq j$
. Let
$\Gamma (f)$
, the Newton boundary of f, be the set of compact boundary faces of
$\Gamma _+ (f)$
, of any dimension. Denote by
$\Gamma ^k (f)$
the set of all k-dimensional faces of
$\Gamma (f) \ (k = 0, \ldots , n - 1)$
. Then
$\Gamma (f) = \bigcup _k \hspace {0.17em} \Gamma ^k (f)$
. For each (compact) face
$S \in \Gamma (f)$
, we define the quasihomogeneous polynomial
$f_S := \sum _{\nu \in S} a_{\nu } z^{\nu }$
. We say f is
$\mathcal {K}\!$
-nondegenerate on S (i.e., nondegenerate in the Kushnirenko sense on S) if the system of polynomial equations
$\frac {\partial f_S}{\partial z_i} = 0 \ (i = 1, \ldots , n)$
has no solutions in
$(\mathbb {C}^{\ast })^n$
; f is
$\mathcal {K}\!$
-nondegenerate if f is
$\mathcal {K}\!$
-nondegenerate on each face
$S \in \Gamma (f)$
.
For each
$(n - 1)$
-dimensional face
$S \in \Gamma ^{n - 1} (f)$
, there exists a vector
$\mathbf {v}_S = (v_1, \ldots , v_n) \in \mathbb {Q}_{> 0}^n$
with positive rational coordinates, perpendicular to S. It is called a normal vector of S and it is unique up to positive scaling. Then
$S = \{x \in \Gamma _+ (f) : \langle \mathbf {v}_S, x \rangle = l_S \}$
, where
$l_S := \inf \{\langle \mathbf {v}_S, x \rangle : x \in \Gamma _+ (f)\}$
. The unique hyperplane
$\Pi _S$
containing S has the equation
$\langle \mathbf {v}_S, x \rangle = l_S$
and it is a supporting hyperplane of
$\Gamma _+ (f)$
. Since
$\mathbf {v}_S$
has positive coordinates,
$\Pi _S$
intersects each coordinate axis
$0 x_i \ (i = 1, \ldots , n)$
in a point whose distance from
$0$
is equal to
$m (S)_{x_i} := \frac {l_S}{v_i}> 0$
. We define
$$\begin{align*}m (S) := \max_i \{ m (S)_{x_i} \} = \max_i \left\{ \frac{l_S}{v_i} \right\}. \end{align*}$$
On the other hand, if
$\mathbf {v} \in \mathbb {Q}_{> 0}^n$
, we define
$l_{\mathbf {v}} := \inf \{\langle \mathbf {v}, x \rangle : x \in \Gamma _+ (f)\}$
and
$S_{\mathbf {v}} := \{x \in \Gamma _+ (f) : \langle \mathbf {v}, x \rangle = l_{\mathbf {v}} \}$
.
$S_{\mathbf {v}}$
is a face of
$\Gamma (f)$
and
$\Pi _{\mathbf {v}}:=\{x \in \mathbb {R}^n : \langle \mathbf {v}, x \rangle = l_{\mathbf {v}} \}$
is a supporting hyperplane of
$\Gamma _+ (f)$
along
$S_{\mathbf {v}}$
(for short,
$\mathbf {v}$
is called a supporting vector along
$S_{\mathbf {v}}$
).
We say
$S \in \Gamma ^{n - 1} (f)$
is exceptional with respect to the axis
$0 x_i$
if one of the partial derivatives
$\frac {\partial f_S}{\partial z_j}$
,
$j \neq i$
, is a pure power of
$z_i$
. Explicitly,
$f_S=a z_i^k z_j+g(z_1, \ldots , z_{j-1},z_{j+1},\ldots ,z_n)$
, where
$a\neq 0$
,
$k \geqslant 1$
. Geometrically, this means S is an
$(n - 1)$
-dimensional pyramid with the base lying in the
$(n - 1)$
-dimensional coordinate hyperplane
$\{ x_j = 0 \}$
, where
$j \neq i$
, and with its apex lying at distance 1 from the axis
$0 x_i$
in the direction of
$0x_j$
(see Figure 1). A face
$S \in \Gamma ^{n - 1} (f)$
is exceptional if S is exceptional with respect to some axis. Let
$\omega \in \{x,y,z\}$
. We denote the set of exceptional faces of f with respect to
$0\omega $
by
$E_{\omega }(f)$
. We denote the set of all exceptional faces of f by
$E (f)$
.
Figure 1 Exceptional faces with respect to the axis
$0 x_i$
.
The main theorem is the following theorem.
Theorem 2.1 If
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
is a
$\mathcal {K}\!$
-nondegenerate isolated surface singularity possessing non-exceptional faces, i.e.,
$\Gamma ^2 (f) \backslash E (f) \neq \varnothing $
, then
$$ \begin{align} \mathcal{L}_0 (f) = \max_{S \in \Gamma^2 (f) \backslash E (f)} m (S) - 1. \end{align} $$
Comments:
-
(1) For
$n = 3$
, the case
$\Gamma ^2 (f) \backslash E (f) = \varnothing $
was established by the third-named author in [Reference OleksikOle13, Theorem 1.8]. Namely, in this case, if we denote the variables in
$\mathbb {C}^3$
by
$x, y, z$
(and permute them if necessary), there is exactly one segment
$S \in \Gamma ^1 (f)$
joining the monomial
$xy$
with some monomial
$z^k$
, where
$k \geqslant 2$
, and then
$\mathcal {L}_0 (f) = k - 1$
. -
(2) The maximum in formula (2.1) may be calculated over the set of certain distinguished non-exceptional faces (see the section “Concluding Remarks”).
-
(3) Lenarcik in [Reference Lejeune-Jalabert and TeissierLen98] proved an alike formula for
$n = 2$
. Precisely,
$$\begin{align*}\mathcal{L}_0 (f) = \left\{\!\!\! \begin{array}{ll} \max_{S \in \Gamma^1 (f) \backslash E (f)} m (S) - 1, & \text{if } \Gamma^1 (f)\ \backslash\ E (f) \neq \varnothing,\\ 1, & \text{if } \Gamma^1 (f)\ \backslash\ E (f) = \varnothing. \end{array} \right. \! \end{align*}$$
-
(4) Directly from the definitions, exceptional faces are always
$\mathcal {K}\!$
-nondegenerate.
As an immediate consequence of Theorem 2.1, we get the following strengthening of the main result of [Reference Brzostowski and OleksikBrz19] (see Theorem 3.1 in the next section).
Corollary 2.2 Let
$f, g : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
be two
$\mathcal {K}\!$
-nondegenerate isolated surface singularities at
$0\in \mathbb {C}^3$
. Assume that
$\varnothing \neq \Gamma ^2 (f)\backslash E(f)=\Gamma ^2 (g) \backslash E(g)$
. Then
$$\begin{align*}\mathcal{L}_0 (f) =\mathcal{L}_0 (g). \end{align*}$$
3 Preliminaries
A crucial role in the proof of the main theorem is played by the following result proved by the first-named author, which can be intuitively rephrased by saying that, in the nondegenerate case,
$\mathcal {L}_0 (f)$
depends only on the Newton polyhedron of f. This observation considerably simplifies the family of singularities we need to consider.
Theorem 3.1 [Reference Brzostowski and OleksikBrz19]
If
$f, g : (\mathbb {C}^n, 0) \rightarrow (\mathbb {C}, 0)$
are
$\mathcal {K}\!$
-nondegenerate isolated singularities and
$\Gamma (f) = \Gamma (g)$
, then
$\mathcal {L}_0 (f) =\mathcal {L}_0 (g)$
.
This theorem, probably known to experts, follows from general facts proved independently by various authors, to mention Damon and Gaffney [Reference Damon and GaffneyDG83], Yoshinaga [Reference YoshinagaYos89], or Oka [Reference OkaOka97, Theorem 5.3].
In the proof of the main theorem, we will apply the celebrated Bernstein theorem on the number of solutions to systems of polynomial equations under some non-degeneracy conditions (so-called Bernstein non-degeneracy). To formulate this theorem, we need to introduce some notions. Let
$f \neq 0$
be a polynomial in n variables
$z_1, \ldots , z_n$
. For each vector
$0 \neq \mathbf {v} \in \mathbb {Z}^n$
, we denote by
$f_{\mathbf {v}}$
the initial part of f (the part of the least degree) with respect to the weights of variables given by the coordinates of
$\mathbf {v}$
. The Newton polytope
$\mathcal {N} (f)$
of f is defined to be the convex hull of
$\operatorname {supp} f$
. Then, the well-known formula holds:
$\mathcal {N} (fg) =\mathcal {N} (f) +\mathcal {N} (g)$
, where the
$+$
denotes the Minkowski sum of subsets of
$\mathbb {R}^n$
. The mixed volume of a system
$(f_1, \ldots , f_n)$
of nonzero polynomials (or of the Newton polytopes
$\mathcal {N} (f_1), \ldots , \mathcal {N} (f_n)$
) is defined by the formula
$$\begin{align*}\operatorname{MV} (f_1, \ldots, f_n) = \sum_{k = 1}^n (- 1)^{n - k} \sum_{I \subset \{1, \ldots, n\}, |I| = k} \operatorname{vol}_n (\sum_{i \in I} \mathcal{N}(f_i)). \end{align*}$$
It is always a nonnegative number. In the case
$n = 2$
, considered in this paper, the above formula takes the simple form
$$\begin{align*}\operatorname{MV} (f_1, f_2) = \operatorname{vol}_2 (\mathcal{N}(f_1) +\mathcal{N}(f_2)) - \operatorname{vol}_2 (\mathcal{N}(f_1)) - \operatorname{vol}_2 (\mathcal{N}(f_2)). \end{align*}$$
Using this formula, it is easy to characterize the pairs
$(f_1, f_2)$
for which
$\operatorname {MV} (f_1, f_2) = 0$
(a general such result one can find, e.g., in [Reference SchneiderSch93, Theorem 5.1.7]).
Lemma 3.2
$\operatorname {MV} (f_1, f_2) = 0$
if and only if either
$\mathcal {N} (f_1)$
and
$\mathcal {N} (f_2)$
are parallel segments or at least one of
$\mathcal {N} (f_1)$
,
$\mathcal {N} (f_2)$
reduces to a point.
The system
$(f_1, \ldots , f_n)$
of polynomials is
$\mathcal {B}$
-nondegenerate (i.e., is nondegenerate in the Bernstein sense) if for each vector
$0 \neq \mathbf {v} \in \mathbb {Z}^n$
the system of equations
${\{(f_1)_{\mathbf {v}} = 0, \ldots , (f_n)_{\mathbf {v}} = 0\}}$
has no solution in
$(\mathbb {C}^{\ast })^n$
.
Theorem 3.3 [Reference BernsteinBer75]
Let
$f_1, \ldots , f_n \in \mathbb {C} [z_1, \ldots , z_n]$
be polynomials. If the mixed volume
$\operatorname {MV} (f_1, \ldots , f_n)$
is positive and the system
$(f_1, \ldots , f_n)$
is
$\mathcal {B}$
-nondegenerate, then the system of equations
$\{f_1 = 0, \ldots , f_n = 0\}$
has only isolated solutions in
$(\mathbb {C}^{\ast })^n$
and their number, counted with multiplicities, is equal to
$\operatorname {MV} (f_1, \ldots , f_n)$
.
Remark. In the original statement of the Bernstein theorem,
$f_i$
may even be Laurent polynomials, i.e., elements of the ring
$\mathbb {C} [z_1, z_1^{- 1}, \ldots , z_n, z_n^{- 1}]$
.
To prove the existence of appropriate paths in
$(\mathbb {C}^3, 0)$
realizing the Łojasiewicz exponent, we will apply the following Maurer theorem, which is a generalization of the classical Puiseux theorem from the two-dimensional case to the n-dimensional one.
Theorem 3.4 [Reference MaurerMau80]
Let
$f_1, \ldots , f_{n - 1} \in \mathfrak {m}\mathcal {O}_n$
be holomorphic function germs defining an analytic curve in
$(\mathbb {C}^n, 0)$
, i.e.,
$\dim \{f_1 = \cdots = f_{n - 1} = 0\} = 1$
. If
$\mathbf {v} \in \mathbb {N}_+^n$
is a vector with positive integer coordinates for which the initial part
$g_{\mathbf {v}}$
of every
$g \in (f_1, \ldots , f_{n - 1}) \mathcal {O}_n$
is not a monomial, then there exists a parametrization
$0 \neq \Phi = (\varphi _1, \ldots , \varphi _n) \in \mathbb {C} \{t\}^n$
,
$\Phi (0) = 0$
, of a branch of
$\{f_1 = \cdots = f_{n - 1} = 0\}$
such that
$(\operatorname {ord} \varphi _1, \ldots , \operatorname {ord} \varphi _n)$
is an integer multiple of
$\mathbf {v}$
.
Finally, the proof of the main theorem makes use of the following criterion for a singularity to be isolated, proved by the first- and third-named authors.
Proposition 3.5 [Reference Brzostowski, Krasiński and SpodziejaBO16, Theorem 3.1 and Proposition 2.6]
Assume that
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
is holomorphic,
$\mathcal {K}\!$
-nondegenerate, and
$\nabla f (0) = 0$
. Then f has an isolated singularity at
$0$
if, and only if, the following conditions hold:
-
(1) f is nearly convenient,
-
(2)
$\operatorname {supp} f$
has points in each of the coordinate planes
$0 xy$
,
$0 xz$
, and
$0 yz$
.
4 Existence of parametrizations for a face
Here and below, in the context of three variables, we shall denote by
$(x, y, z)$
both the coordinates in
$\mathbb {C}^3$
(the domain of singularities) and coordinates in
$\mathbb {R}^3$
(the space for the Newton polyhedrons). It will always be clear from the context to which space they are referring to. Moreover, we let
$$ \begin{align} \overline{g} (y, z) := g (1, y, z) \in \mathbb{C} [y, z], \end{align} $$
for any polynomial
$g \in \mathbb {C} [x, y, z]$
. Then, obviously,
$\overline {\frac {\partial g}{\partial y}} = \frac {\partial \overline {g}}{\partial y}$
and
$\overline {\frac {\partial g}{\partial z}} = \frac {\partial \overline {g}}{\partial z}$
.
The main result of this section is the following theorem, which assures, under certain non-degeneracy conditions on a two-dimensional face of an isolated surface singularity, that one can find a parametrization of a branch of a polar curve whose initial exponent vector (i.e., its vector of orders) is perpendicular to the aforementioned face. This theorem may also be viewed as a generalization of the Newton–Puiseux theorem from
$2$
to
$3$
indeterminates in the case of polar curves.
Theorem 4.1 Let
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
be an isolated singularity, and let S be a two-dimensional face of
$\Gamma (f)$
with a normal vector
$\mathbf {v} \in \mathbb {Q}^3_{> 0}$
. Assume that
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})> 0$
and the pair
$(\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})$
is
$\mathcal {B}$
-nondegenerate. Assume, moreover, that f is
$\mathcal {K}\!$
-nondegenerate on all the edges of S. Then there exists a parametrization
$0 \neq \Phi = (\varphi _1, \varphi _2, \varphi _3) \in \mathbb {C} \{t\}^3$
,
$\Phi (0) = 0$
, of a branch of the curve
$\{ \frac {\partial f}{\partial y} = 0, \frac {\partial f}{\partial z} = 0\}$
such that
$(\operatorname {ord} \varphi _1, \operatorname {ord} \varphi _2, \operatorname {ord} \varphi _3)$
is proportional to
$\mathbf {v}$
.
To prove this theorem, we need two lemmas. The first one is a generalization of a well-known, two-dimensional criterion of the Kushnirenko non-degeneracy which reads: if
$F \in \mathbb {C} [x, y]\ \backslash\ \mathbb {C}$
is a quasihomogeneous polynomial (with positive rational weights), then F is
$\mathcal {K}\!$
-degenerate if, and only if, its partial derivatives have a common non-monomial factor (equivalently: F has a multiple non-monomial factor).
Lemma 4.2 Let
$F \in \mathbb {C} [x, y, z]\ \backslash\ \mathbb {C}$
be a quasihomogeneous polynomial (with positive rational weights). If at least two its partial derivatives have a common non-monomial factor and
$\dim \mathcal {N} (F) = 2$
, then F is
$\mathcal {K}\!$
-degenerate on an edge of
$\mathcal {N} (F)$
.
In this lemma, as F is quasihomogeneous,
$\Gamma ^2 (F)$
consists of only one two-dimensional face, say S. Thus,
$\Gamma ^2 (F) = \{ S \}$
,
$\mathcal {N} (F) = S$
and
$F = F_S$
. In the course of its proof, we find it convenient to project the face S to the plane
$0 y z$
. It is important to note that, as S has a normal vector with positive coordinates, this projection
$\operatorname {pr}_{y, z}$
, when restricted to S, is a bijection and respects the edges of S: T is an edge of S if, and only if,
$\operatorname {pr}_{y, z} (T)$
is an edge of
$\operatorname {pr}_{y, z} (S)$
.
Proof of Lemma 4.2
As above, we have
$F = F_S$
, where
$S =\mathcal {N} (F)$
. W may choose
$\mathbf {u} = (u_x, u_y, u_z) \in \mathbb {N}_+^3$
perpendicular to S; then F is quasihomogeneous with respect to the weights defined by
$\mathbf {u}$
. Up to renaming of the variables, we can write
$$\begin{align*}\frac{\partial F}{\partial y} = PQ_1,\ \ \frac{\partial F}{\partial z} = PQ_2 \end{align*}$$
in
$\mathbb {C} [x, y, z]$
, where P is not a monomial and
$P, Q_1, Q_2 \in \mathbb {C} [x, y, z]$
are quasihomogeneous with respect to the same vector of weights
$\mathbf {u}$
.
We will show that F can be brought to a special form. First, we may assume F is homogeneous. In fact, if we define
$\tilde {F} (x, y, z) := F (x^{u_x}, y^{u_y}, z^{u_z})$
, then
$\tilde {F}$
is a homogeneous polynomial,
$\dim \mathcal {N} (\tilde {F}) = 2$
, and the
$\mathcal {K}\!$
-non-degeneracies of
$\tilde {F}$
on
$\mathcal {N} (\tilde {F})$
and F on
$\mathcal {N}(F) = S$
(and on their corresponding boundary edges) are equivalent. Moreover,
$\frac {\partial \tilde {F}}{\partial y}$
and
$\frac {\partial \tilde {F}}{\partial z}$
still have a non-monomial factor in common, viz.,
$P (x^{u_x}, y^{u_y}, z^{u_z})$
.
After this simplification, we return to the original notations. Thus, F is homogeneous of a degree
$\alpha> 0$
,
$\frac {\partial F}{\partial y} = P Q_1$
,
$\frac {\partial F}{\partial z} = PQ_2$
in
$\mathbb {C} [x, y, z]$
,
$P, Q_1, Q_2$
are homogeneous, and P is not a monomial. Putting
$x = 1$
, we get
$\frac {\partial \overline {F}}{\partial y} = \overline {P} \, \overline {Q}_1$
and
$\frac {\partial \overline {F}}{\partial z} = \overline {P} \, \overline {Q}_2$
in
$\mathbb {C} [y, z]$
. As P is homogeneous and not a monomial,
$\overline {P}$
is not a monomial, either. Exchanging
$\overline {P}$
for its irreducible, non-monomial factor, we may additionally assume that
$\overline {P}$
itself is irreducible in
$\mathbb {C} [y, z]$
. From the Freudenburg lemma ([Reference FreudenburgFre96] or [Reference van den Essen, Nowicki and TycvdENT03, Corollary 3.2]), then, we infer that
$\overline {F} = \overline {P}^2 R_0 + c$
, where
$R_0 \in \mathbb {C} [y, z]$
and
$c \in \mathbb {C}$
. Hence,
$$\begin{align*}F (x, y, z) = x^{\alpha} \overline{F} (\frac{y}{x}, \frac{z}{x}) = P^2 (x, y, z) R (x, y, z) + cx^{\alpha}, \end{align*}$$
where the homogeneous
$R \in \mathbb {C} [x, y, z]$
satisfies
$\overline {R} = R_0$
.
Passing to the proof of the degeneracy of F, we may assume
$c \neq 0$
; for otherwise, the assertion is clear. Utilizing the form of F, we shall indicate an edge T of S for which
$F_T$
has a double, non-monomial factor; then F will be
$\mathcal {K}\!$
-degenerate on T. More precisely, we shall find an edge
$T_0$
of
$\mathcal {N} (P)$
whose supporting vector
$\mathbf {v}$
defines an edge
$T=T_{\mathbf {v}}$
of S not passing through the point
$x^{\alpha }$
. Then
$F_T = F_{\mathbf {v}} = (P^2 \cdot R)_{\mathbf {v}} = (P_{T_0})^2 \cdot R_{\mathbf {v}}$
and F is
$\mathcal {K}\!$
-degenerate on
$T \in \Gamma ^1 (F)$
. This goal can be achieved by projecting S to the plane
$0 y z$
and finding there an edge
$\tilde {T}_0$
of
$\mathcal {N} (\overline {P})$
whose supporting vector
$\tilde {\mathbf {v}}$
defines an edge
$\tilde {T}$
of
$\overline {S} := \operatorname {pr}_{y, z} (S)$
not passing through the point
$(0, 0)$
. Indeed, having such a
$\tilde {T}$
and
$\tilde {\mathbf {v}}$
, it is enough to set
$T := \operatorname {pr}_{y, z}^{- 1} (\tilde {T}) \cap S$
and
$\mathbf {v} := (0, \tilde {v}_1, \tilde {v}_2)$
, and then the above calculation for
$F_T$
applies.
We have
$\overline {F} := \overline {P}^2 \overline {R} + c$
. As S is a two-dimensional face,
$\overline {S}$
is also two-dimensional. Similarly, as P is not a monomial,
$\mathcal {N} (\overline {P})$
is at least a segment. It is convenient to distinguish two possibilities on the shape of the Newton polytope
$\mathcal {N} (\overline {P})$
of
$\overline {P}$
:
1st case:
$\mathcal {N} (\overline {P})$
is a segment. Let
$\mathbf {{\textbf {w}}} \in \mathbb {Z}^2 \backslash \{ 0 \}$
be a vector perpendicular to
$\overline {P}$
. If
$\operatorname {ord}_{\mathbf {w}} (\overline {P}^2 \overline {R}) < 0$
, then
$\overline {F}_{\mathbf {w}} = (\overline {P}^2 \overline {R})_{\mathbf {w}} = \overline {P}^2 \overline {R}_w$
. Hence, we may set
$\tilde {T}_0 := \mathcal {N} (\overline {P})$
and
$\tilde {\mathbf {v}} := \mathbf {w}$
in this case. If
$\operatorname {ord}_{\mathbf {w}} (\overline {P}^2 \overline {R}) \geqslant 0$
, then we have
$\operatorname {ord}_{- \mathbf {w}} (\overline {P}^2 \overline {R} + c) = - \deg _{\mathbf {w}} (\overline {P}^2 \overline {R} + c) \leqslant - \operatorname {ord}_{\mathbf {w}} (\overline {P}^2 \overline {R} + c) \leqslant 0$
. But then we must have
$\operatorname {ord}_{- \mathbf {w}} (\overline {P}^2 \overline {R}) < 0$
for, otherwise,
$\overline {S}$
would be a segment. Now, as above, we may take
$\tilde {T}_0 := \mathcal {N} (\overline {P})$
and
$\tilde {\mathbf {v}} := - \mathbf {w}$
.
2nd case:
$\mathcal {N} (\overline {P})$
is a two-dimensional polygon. Let
$T_1, \ldots , T_k$
be boundary edges of
$\mathcal {N} (\overline {P})$
and
$\mathbf {v}_1, \ldots , \mathbf {v}_k \in \mathbb {Z}^2 \backslash \{ 0 \}$
, respectively, their (inward-pointing) normal vectors (so that
$\overline {P}_{\mathbf {v}_i} = \overline {P}_{T_i}$
) (see Figure 2a). These vectors also define the corresponding edges of
$\mathcal {N} (\overline {P}^2 \overline {R})$
, namely,
$\tilde {T}_i := \mathcal {N} \left ( (\overline {P}^2 \overline {R})_{\mathbf {v}_i} \right ) \ (i = 1, \ldots , k)$
. Clearly,
$\tilde {T}_1, \ldots , \tilde {T}_k$
are parallel to
$T_1, \ldots , T_k$
, respectively. Since
$\mathbf {v}_1, \ldots , \mathbf {v}_k$
is a collection of normal vectors of all the edges of a two-dimensional convex polygon
$\mathcal {N} (\overline {P})$
and the polygon
$\mathcal {N} (\overline {P}^2 \overline {R})$
is also convex, the edges
$\tilde {T}_1, \ldots , \tilde {T}_k$
of
$\mathcal {N} (\overline {P}^2 \overline {R})$
can be prolonged to form a convex polygon too (see Figure 2b).
Figure 2 (a) The polygon
$\mathcal {N} (\overline {P})$
. (b) The polygon
$\mathcal {N} (\overline {P}^2 \overline {R})$
and prolongations of
$\tilde {T}_i$
.
But
$\overline {S} =\mathcal {N} (\overline {P}^2 \overline {R} + c) = \operatorname {conv} (\mathcal {N}(\overline {P}^2 \overline {R}) \cup \{(0, 0)\})$
, so at least one of the edges
$\tilde {T}_1, \ldots , \tilde {T}_k$
of
$\mathcal {N} (\overline {P}^2 \overline {R})$
is also an edge of
$\overline {S}$
, one not passing through the point
$(0, 0)$
. Say it is
$\tilde {T}_1$
. Then we may set
$\tilde {T} := \tilde {T}_1$
and
$\tilde {\mathbf {v}} := \mathbf {v}_1$
in this case.
Remark. It would be interesting to know if the above lemma holds, mutatis mutandis, in the n-dimensional case.
The second lemma is of algebraic nature.
Lemma 4.3 Let R be a unique factorization domain,
$F, G \in R [[X_1, \ldots , X_n]] \backslash \{ 0 \}$
and
$\mathbf {v} \in \mathbb {N}_+^n$
, where
$n \geqslant 3$
. Assume that
$F_{\mathbf {v}}, G_{\mathbf {v}}$
have no common divisor in
$R [X_1, \ldots , X_n]$
except monomials, and the ideal
$\left ( F_{\mathbf {v}}, G_{\mathbf {v}} \right )$
in
$R [X_1, \ldots , X_n]$
does not contain any monomial. Then the ideal
$(F, G) \subset R [[X_1, \ldots , X_n]]$
does not contain any element H such that
$H_{\mathbf {v}}$
is a monomial.
Remark. Here, just as everywhere else in the paper, we do not demand a monomial to be monic. However, the lemma is still valid, with the same proof, if we do impose this restriction in both the assumptions and in the assertion of the lemma (simultaneously).
Proof of Lemma 4.3
First, let us introduce a piece of notation: let
$\mathfrak {S} := R [[X_1, \ldots , X_n]]$
and, for an ideal
$\mathcal {I} \subset \mathfrak {S}$
, let
$\operatorname {in}_{\mathbf {v}} \mathcal {I} := \left \{ g_{\mathbf {v}} : g \in \mathcal {I} \right \} \mathfrak {S}$
be the
$\mathbf {v}$
-initial ideal of
$\mathcal {I}$
.
To the contrary, say there exists a monomial
$\omega \in \operatorname {in}_{\mathbf {v}} (F, G)$
. Then
$$ \begin{align} AF + BG = \omega + \text{h.o.t.}, \end{align} $$
for some A,
$B \in \mathfrak {S}$
. Here,
$A \neq 0 \neq B$
by the second assumption.
As a first reduction, we may think
$\operatorname {ord}_{\mathbf {v}} F = \operatorname {ord}_{\mathbf {v}} G$
. For this, it is enough to consider
$X^{\alpha } F$
and
$X^{\beta } G$
instead of F and G (respectively), where
$X^{\alpha }$
is a monomial appearing in
$G_{\mathbf {v}}$
and
$X^{\beta }$
is a monomial appearing in
$F_{\mathbf {v}}$
. Then, a relation of type (4.2) still holds with
$\omega $
modified to
$X^{\alpha + \beta } \omega $
.
Secondly, we may assume
$F_{\mathbf {v}}$
and
$G_{\mathbf {v}}$
to be co-prime. Indeed, write
$F = F_{\mathbf {v}} + F'$
,
$G = G_{\mathbf {v}} + G'$
and let
$\varrho := \gcd \left ( F_{\mathbf {v}}, G_{\mathbf {v}} \right )$
be the common monomial divisor. Substituting
$\varrho ^{v_i} X_i$
for
$X_i$
(
$i = 1, \ldots , n$
), where
$\mathbf {v} = (v_1, \ldots , v_n)$
, from (4.2), we get
$\tilde {A} \left ( F_{\mathbf {v}} + \rho \tilde {F}' \right ) + \tilde {B} \left ( G_{\mathbf {v}} + \rho \tilde {G}' \right ) = \varrho ^t \left ( \omega + \text {h.o.t.} \right )$
, where
$t = \deg _{\mathbf {v}} \omega $
and
$\tilde {A}, \tilde {B}, \tilde {F}', \tilde {G}' \in \mathfrak {S}$
. By assumption, there are no monomials in the ideal
$\left ( F_{\mathbf {v}}, G_{\mathbf {v}} \right )$
; thus,
$t> 0$
. Hence,
$\tilde {A} \left ( \frac {F_{\mathbf {v}}}{\varrho } + \tilde {F}' \right ) + \tilde {B} \left ( \frac {G_{\mathbf {v}}}{\varrho } + \tilde {G}' \right ) = \varrho ^{t - 1} \omega + \text {h.o.t.}$
Replacing F by
$\frac {F_{\mathbf {v}}}{\varrho } + \tilde {F}'$
, G by
$\frac {G_{\mathbf {v}}}{\varrho } + \tilde {G}'$
, and
$\omega $
by
$\varrho ^{t - 1} \omega $
, we easily see that, still, all the assumptions of the lemma hold for the changed F, G but now
$\gcd \left ( F_{\mathbf {v}}, G_{\mathbf {v}} \right ) = 1$
; moreover, we still have
$\operatorname {ord}_{\mathbf {v}} F = \operatorname {ord}_{\mathbf {v}} G$
and relation of type (4.2).
Let
$\xi := \operatorname {ord}_{\mathbf {v}} F = \operatorname {ord}_{\mathbf {v}} G$
,
$t := \operatorname {ord}_{\mathbf {v}} \omega $
, and let
$F = \sum _{i \geqslant \xi } F^{(i)}$
,
$G = \sum _{i \geqslant \xi } G^{(i)}$
,
$A = \sum _{i \geqslant \delta } A^{(i)}$
,
$B = \sum _{i \geqslant \eta } B^{(i)}$
be the decompositions of the involved series into their quasihomogeneous components for the gradation defined by the weight vector
$\mathbf {v}$
. Thus,
$F^{(\xi )} = F_{\mathbf {v}}$
and
$G^{(\xi )} = G_{\mathbf {v}}$
. Notice that
$\operatorname {ord}_{\mathbf {v}} A \geqslant \xi $
and
$\operatorname {ord}_{\mathbf {v}} B \geqslant \xi $
, too. Indeed, the (nonzero) components of lowest degree of
$AF$
and
$BG$
are, respectively, equal to
$A^{(\delta )} F^{(\xi )}$
and
$B^{(\eta )} G^{(\xi )}$
; clearly,
$\min (\delta + \xi , \eta + \xi ) \leqslant t$
. This inequality must be strict because of our second assumption. But then, as
$A^{(\delta )} \neq 0 \neq B^{(\eta )}$
, we get
$\delta = \eta $
and
$A^{(\delta )} F^{(\xi )} + B^{(\eta )} G^{(\xi )} = 0$
. Since
$R [X_1, \ldots , X_n]$
is a UFD and
$\gcd (F^{(\xi )}, G^{(\xi )}) = 1$
, we infer that
$F^{(\xi )} \mathrel {|} B^{(\eta )}$
and
$G^{(\xi )} \mathrel {|} A^{(\delta )}$
; hence,
$\xi \leqslant \eta $
,
$\xi \leqslant \delta $
, and
$2 \xi < t$
.
Set
$C^{(2 \xi + n)} := \sum _{0 \leqslant i \leqslant n} (A^{(\xi + i)} F^{(\xi + n - i)} + B^{(\xi + i)} G^{(\xi + n - i)})$
, for
$n \geqslant 0$
. By the above,
$C^{(2 \xi + n)}$
is the component of degree
$(2 \xi + n)$
of the left-hand side of (4.2). We shall construct a sequence
$(P^{(j)})_{0 \leqslant j \leqslant t - 2 \xi - 1}$
of quasihomogeneous polynomials
$P^{(j)} \in R [X_1, \ldots , X_n]$
of
$\mathbf {v}$
-degree j such that
$$ \begin{align} \left\{\!\!\begin{array}{lll} A^{(\xi + n)} = \sum_{0 \leqslant j \leqslant n} P^{(j)} G^{(\xi + n - j)}\\B^{(\xi + n)} = - \sum_{0 \leqslant j \leqslant n} P^{(j)} F^{(\xi + n - j)} \end{array} \right.\!\!\!\!\!, \text{ for } 0 \leqslant n \leqslant t - 2 \xi - 1. \end{align} $$
We have
$2 \xi < t$
so, as above, we get
$0 = C^{(2 \xi )} = A^{(\xi )} F^{(\xi )} + B^{(\xi )} G^{(\xi )}$
. Thus, we may set
$P^{(0)} := A^{(\xi )} / G^{(\xi )} = - B^{(\xi )} / F^{(\xi )} \in R [X_1, \ldots , X_n]$
. Then (4.3) holds with
$n = 0$
.
Say, we have already defined
$(P^{(j)})_{0 \leqslant j \leqslant N - 1}$
for some
$1 \leqslant N \leqslant t - 2 \xi $
. We have
$$ \begin{align*} C^{(2 \xi + N)} &= \sum_{0 \leqslant i \leqslant N} (A^{(\xi + i)} F^{(\xi + N - i)} + B^{(\xi + i)} G^{(\xi + N - i)}) =\\ &= A^{(\xi + N)} F^{(\xi)} + B^{(\xi + N)} G^{(\xi)}+\\ &+ \sum_{0 \leqslant i \leqslant N - 1}\,\, \sum_{0 \leqslant j \leqslant i} (P^{(j)} G^{(\xi + i - j)} F^{(\xi + N - i)} - P^{(j)} F^{(\xi + i - j)} G^{(\xi + N - i)}) =\\ &= A^{(\xi + N)} F^{(\xi)} + B^{(\xi + N)} G^{(\xi)}+\\ &+ \sum_{0 \leqslant j \leqslant N - 1} P^{(j)} \sum_{j \leqslant i \leqslant N - 1} (G^{(\xi + i - j)} F^{(\xi + N - i)} - F^{(\xi + i - j)} G^{(\xi + N - i)}). \end{align*} $$
After interchanging the order of the summands, the inner sum becomes
$$ \begin{align*} \sum_{j \leqslant i \leqslant N - 1} G^{(\xi + i - j)} F^{(\xi + N - i)} - \sum_{j + 1 \leqslant i \leqslant N} F^{(\xi + N - i)} G^{(\xi + i - j)} &=\\ =G^{(\xi)} F^{(\xi + N - j)} &- F^{(\xi)} G^{(\xi + N - j)}. \end{align*} $$
Hence,
$$ \begin{align*} C^{(2 \xi + N)} & = A^{(\xi + N)} F^{(\xi)} + B^{(\xi + N)} G^{(\xi)} +\\ &+ \sum_{0 \leqslant j \leqslant N - 1} P^{(j)} (G^{(\xi)} F^{(\xi + N - j)} - F^{(\xi)} G^{(\xi + N - j)})=\\ & = F^{(\xi)} \left( A^{(\xi + N)} - \sum_{0 \leqslant j \leqslant N - 1} P^{(j)} G^{(\xi + N - j)} \right)+\\ &+{}G^{(\xi)} \left( B^{(\xi + N)} + \sum_{0 \leqslant j \leqslant N - 1} P^{(j)} F^{(\xi + N - j)} \right). \end{align*} $$
If
$N \leqslant t - 2 \xi - 1$
, then
$C^{(2 \xi + N)} = 0$
and, as above, using the fact that
$R [X_1, \ldots , X_n]$
is a UFD and
$\gcd (F^{(\xi )}, G^{(\xi )}) = 1$
, we define
$P^{(N)}$
by
$P^{(N)} G^{(\xi )} = A^{(\xi + N)} - \sum _{0 \leqslant j \leqslant N - 1} P^{(j)} G^{(\xi + N - j)}$
. But then, from the above equality, we get
$$ \begin{align*} 0 = P^{(N)} F^{(\xi)} + B^{(\xi + N)} + \sum_{0 \leqslant j \leqslant N - 1} P^{(j)} F^{(\xi + N - j)}. \end{align*} $$
Hence, (4.3) holds with
$n = N$
. Consequently, the sequence
$(P^{(j)})_{0 \leqslant j \leqslant t - 2 \xi - 1}$
is defined by induction.
If
$N = t - 2 \xi $
, then
$C^{(2 \xi + N)} = \omega $
. This gives
$\omega \in (F^{(\xi )}, G^{(\xi )}) R [X_1, \ldots , X_n]$
; contradiction.
Now, we can give the following.
Proof of Theorem 4.1
Clearly, we may assume that
$\mathbf {v} = (v_x, v_y, v_z) \in \mathbb {N}_+^3$
. We have
$f_S = f_{\mathbf {v}}$
. Since S is a two-dimensional face and
$\mathbf {v}$
has positive coordinates,
$f_S$
depends in an essential way on y and z, i.e.,
$\frac {\partial f_S}{\partial y} \neq 0$
and
$\frac {\partial f_S}{\partial z} \neq 0$
. Hence,
$\frac {\partial f_S}{\partial y} = \frac {\partial f_{\mathbf {v}}}{\partial y} = (\frac {\partial f}{\partial y})_{\mathbf {v}}$
and
$\frac {\partial f_S}{\partial z} = \frac {\partial f_{\mathbf {v}}}{\partial z} = (\frac {\partial f}{\partial z})_{\mathbf {v}}$
. In view of the assumptions and the Bernstein theorem (Theorem 3.3), the pair
$\{ \frac {\partial \overline {f_S}}{\partial y} = 0, \frac {\partial \overline {f_S}}{\partial z} = 0\}$
possesses
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})> 0$
solutions in
$(\mathbb {C}^{\ast })^2$
. Hence,
$\{ \frac {\partial f_S}{\partial y} = 0, \frac {\partial f_S}{\partial z} = 0\}$
possesses solutions in
$(\mathbb {C}^{\ast })^3$
. This means that in the ideal
$((\frac {\partial f}{\partial y})_{\mathbf {v}}, (\frac {\partial f}{\partial z})_{\mathbf {v}}) \mathcal {O}_3 = (\frac {\partial f_S}{\partial y}, \frac {\partial f_S}{\partial z}) \mathcal {O}_3$
there are no monomials.
Moreover, applying Lemma 4.2 to
$F = f_S$
, we infer that
$\frac {\partial f_S}{\partial y}, \frac {\partial f_S}{\partial z}$
have no common factor in
$\mathbb {C} [x, y, z]$
except a monomial.
Summing up, we have checked that the pair
$\frac {\partial f}{\partial y}, \frac {\partial f}{\partial z}$
in
$\mathcal {O}_3 =\mathbb {C} \{x, y, z\}$
, and the weight vector
$\mathbf {v}$
fulfill the assumptions of Lemma 4.3. Therefore,
$\frac {\partial f}{\partial y}$
and
$\frac {\partial f}{\partial z}$
do not generate any element in
$\mathcal {O}_3$
with initial
$\mathbf {v}$
-part being a monomial. This, in turn, means we are in the position to apply the Maurer theorem (Theorem 3.4) to the curve
$\{ \frac {\partial f}{\partial y} = 0, \frac {\partial f}{\partial z} = 0\}$
and the vector
$\mathbf {v}$
. Thus, we are delivered the required parametrization
$\Phi $
.
Although generic, the Bernstein non-degeneracy is a necessary assumption in Theorem 4.1 (it does not follow from Kushnirenko non-degeneracy). This is illustrated by the following.
Example 4.4 Let
$f := (x^4 + y^3) z + x^4 y + \frac {1}{4} y^4 + x^6 + z^5$
. Then
$\Gamma ^2 (f)$
is built of three faces, two of which are non-exceptional. Consider the face
$S := \mathcal {N} \Big( (x^4 + y^3) z + x^4 y + \frac {1}{4} y^4 \Big )$
, a parallelogram in space. As its normal vector, we may take
$\mathbf {v} := (3, 4, 4)$
. It is easy to check that f is
$\mathcal {K}\!$
-nondegenerate. We have
$\left ( \tfrac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z} \right ) = (1 + y^3 + 3 y^2 z, 1 + y^3)$
. Hence,
$\operatorname {MV} \left ( \tfrac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z} \right ) = 3> 0$
. However,
$\left \{ \tfrac {\partial \overline {f_S}}{\partial y} = \frac {\partial \overline {f_S}}{\partial z} = 0 \right \} \subset \{ z = 0 \}$
so the system has no solutions in
$(\mathbb {C}^{\ast })^2$
. A fortiori, there are no parametrizations of
$\left \{ \tfrac {\partial f}{\partial y} = \frac {\partial f}{\partial z} = 0 \right \}$
with initial exponent vector proportional to
$\mathbf {v}$
, contrary to the assertion of Theorem 4.1. The reason behind this is that the system
$\left \{ \tfrac {\partial \overline {f_S}}{\partial y} = \frac {\partial \overline {f_S}}{\partial z} = 0 \right \}$
is
$\mathcal {B}$
-degenerate: for the vector
$\mathbf {w} := (0, 1) \in \mathbb {N}^2$
, we have
$\left ( \tfrac {\partial \overline {f_S}}{\partial y} \right )_{\mathbf {w}} = \left ( \frac {\partial \overline {f_S}}{\partial z} \right )_{\mathbf {w}} = 1 + y^3$
, proving the degeneracy. Note also that S is a proximate face for the axis
$0 x$
(see Definition 5.1).
It turns out that under some further restrictions, including ones on the geometry of the face, we may avoid the misbehavior from the above example. Namely, we have the following.
Theorem 4.5 Let
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
be an isolated singularity, and let
$S \in \Gamma ^2 (f)$
satisfy
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})> 0$
. Assume that no edges of S have prolongations intersecting the axis
$0 x$
, except, perhaps, those having a vertex in
$0 x y \cup 0 x z$
. Assume, moreover, that
$f_S$
has generic coefficients and
$\operatorname {supp} f_S = \Gamma ^0 (f_S)$
. Then there exists a parametrization
$0 \neq \Phi = (\varphi _1, \varphi _2, \varphi _3) \in \mathbb {C} \{t\}^3$
of a branch of the curve
$\{ \frac {\partial f}{\partial y} = 0, \frac {\partial f}{\partial z} = 0\}$
at
$0$
, whose initial exponent vector is perpendicular to S.
The above theorem follows directly from Theorem 4.1, genericness of
$\mathcal {K}\!$
-non-degeneracy (see [Reference Kuo and LuKou76, Reference OkaOka79]), and the following observation.
Lemma 4.6 Under the above assumptions, the pair
$(\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})$
is
$\mathcal {B}$
-nondegenerate.
Proof Take any
$\mathbf {w} = (w_1, w_2) \in \mathbb {Z}^2 \backslash \{0\}$
and consider the system of equations
$$ \begin{align} \left( \frac{\partial \overline{f_S}}{\partial y} \right)_{\mathbf{w}} = \left( \frac{\partial \overline{f_S}}{\partial z} \right)_{\mathbf{w}} = 0. \end{align} $$
We must show that this system has got no solutions in
$(\mathbb {C}^{\ast })^2$
. Since
$\operatorname {supp}f_S$
is equal to the set of vertices of S, the polynomials
$(\frac {\partial \overline {f_S}}{\partial y})_{\mathbf {w}}$
and
$(\frac {\partial \overline {f_S}}{\partial z})_{\mathbf {w}}$
are monomials or binomials only. Clearly, it suffices to consider the case both of them are binomials. Then their supports define parallel segments. If these binomials are not partial derivatives of one and the same edge (or diagonal) of
$\overline {f_S}$
, then, because of genericness of coefficients of
$f_S$
and the parallelity of the segments, system (4.4) has got no solutions in
$(\mathbb {C}^{\ast })^2$
. In the opposite case, we have
$(\frac {\partial \overline {f_S}}{\partial y})_{\mathbf {w}} = \frac {\partial \overline {f_T}}{\partial y}$
,
$(\frac {\partial \overline {f_S}}{\partial z})_{\mathbf {w}} = \frac {\partial \overline {f_T}}{\partial z}$
, where T is an edge or a diagonal of S (the latter may happen if some
$x^i \in \operatorname {supp} f_S$
). The polynomial
$f_T$
is also a binomial. As
$\frac {\partial f_T}{\partial y}$
and
$\frac {\partial f_T}{\partial z}$
are binomials, the segment T is disjoint from both coordinate planes
$0 x y$
,
$0 x z$
. If
$T \in \Gamma ^1 (f_S)$
, then, directly by the assumption, we get that the line containing T does not intersect the axis
$0 x$
. If this is not the case, viz., T is a diagonal of S, the only possibility is that T connects the two vertices of
$\mathcal {N} (f_S)$
joined by edges with
$x^i$
(as
$\operatorname {supp} f_S = \Gamma ^0 (f_S)$
). Thus, also in this situation, the line containing T does not intersect the axis
$0 x$
.
Clearly,
$\overline {f_T}$
takes one of the following two forms: (1)
$y^l z^m (\alpha y^a + \beta z^b)$
, with
$l, m, a, b> 0$
, or (2)
$y^l z^m (\alpha + \beta y^a z^b)$
, with
$l, m> 0$
,
$a + b> 0$
, where the coefficients
$\alpha , \beta $
are generic. An easy analysis leads to the conclusion that the system
$\{ \frac {\partial \overline {f_T}}{\partial y} = 0, \frac {\partial \overline {f_T}}{\partial z} = 0\}$
has got a solution in
$(\mathbb {C}^{\ast })^2$
if and only if
$\overline {f_T}$
is of the second form, where, moreover,
$a, b> 0$
and
$\frac {k}{l} = \frac {a}{b}$
. This last condition, however, means the prolongation of T intersects the axis
$0 x$
; impossible.
5 The geometry of proximity faces
Let
$g:(\mathbb {C}^3, 0) \rightarrow (\mathbb {C},0)$
be an isolated singularity and
$\omega \in \{x,y,z\}.$
If
$\Gamma ^2(g)\backslash E_{\omega }(g) \neq \varnothing $
, the maximal
$m (S)_\omega $
among
$S\in \Gamma ^2 (g)\backslash E_\omega (g)$
is always achieved on an
$0 \omega $
-non-exceptional face of a special type, a face—in a sense—“closest” to one of the coordinate axes (see Lemma 5.6). Moreover, then, there are certain restrictions on the geometry of such a face. This leads to the following definition.
Definition 5.1 Let
$\omega \in \{x, y, z\}$
. We say that
$S \in \Gamma ^2 (g)$
is proximate for the axis
$ 0\omega $
if S is non-exceptional with respect to the axis
$0 \omega $
, has a vertex lying at distance
$\leqslant 1$
from this axis, and touches both coordinate planes containing this axis. A proximity face is one which is proximate for one of the axes.
In particular, according to the above definition, a face that is
$0 \omega $
-non-exceptional and has a vertex on the axis
$0 \omega $
is
$0 \omega $
-proximate. The existence of a proximity face for some axis is characterized by the two following propositions. They are simple consequences of Lemma 3.1 and Theorem 3.8 in [Reference OleksikOle13].
Proposition 5.2 Let
$\omega \in \{x,y,z\}.$
There exists a proximity face for
$0\omega $
if, and only if,
$\Gamma ^2(g)\backslash E_{\omega }(g)\neq \varnothing .$
Moreover, if
$\Gamma ^2(g)\backslash E(g)\neq \varnothing $
, then all the proximity faces are non-exceptional.
Proposition 5.3 Let
$\omega \in \{ x, y, z \}$
. The following conditions are equivalent:
-
(1)
$\Gamma ^2 (g) \backslash E_{\omega } (g) = \varnothing $
. -
(2)
$E (g) = E_{\omega } (g)$
and, up to permutation of the variables
$(x, y, z)$
, there exists an edge
$\mathcal {N} (x {} y + z^{\alpha }) \in \Gamma ^1 (g)$
, for some
$\alpha \geqslant 2$
.
It is easy to observe that a face can be exceptional with respect to one of the axes only, i.e.,
$E_x(g)\cap E_y(g)=\varnothing $
,
$E_x(g)\cap E_z(g)=\varnothing $
,
$E_y(g)\cap E_z(g)=\varnothing $
. Hence, assuming
$\Gamma ^2 (g) \neq \varnothing $
, by Proposition 5.2, there exist proximity faces for g for at least two coordinate axes. But not necessarily for all three axes, as the following example shows.
Example 5.4 In a typical situation, a proximity face S is non-exceptional; in general, however, this is not the case, e.g.,
$S := \mathcal {N} (g)$
, where
$g := xz + yz + y^3$
, is
$0 x$
-proximate but
$\frac {\partial g}{\partial x} = z$
so S is exceptional with respect to the axis
$0 z$
. This also means that the isolated singularity g does not have any proximity face for the axis
$0 z$
. Observe that, by Proposition 5.2, this phenomenon can only happen if
$\Gamma ^2 (g) \backslash E (g)=\varnothing $
.
Let
$S\in \Gamma ^2 (g)$
be proximate for, say, the axis
$0 x$
. One can observe that two situations may occur (cf. [Reference OleksikOle13, Lemma 3.1 and Property 3.3]):
-
a) S is convenient with respect to the axis
$0 x$
(i.e., S touches
$0 x$
) and then this proximity face is not necessarily unique for
$0 x$
(see Figure 3a). In this case, all the faces proximate for the axis
$0 x$
share one common vertex,
$x^{m (S)_x}$
.Figure 3 Proximity faces S for the axis
$0 x$
: (a)
$S$
convenient, (b)
$S$
non-convenient. -
b) S is non-convenient with respect to the axis
$0 x$
(i.e., S is disjoint from
$0 x$
); then it is unique and has an edge joining some monomials of the form
$x^k z$
,
$k \geqslant 1$
, and
$x^m y^n$
,
$m \geqslant 0, n \geqslant 1$
(or similar monomials with the variables y and z permuted). Moreover, in
$\operatorname {supp} g$
restricted to the plane
$0 x y$
, the point
$x^m y^n$
has the smallest possible y-coordinate among all
$0 x$
-non-exceptional faces (see Figure 3b).
Note that, in both above situations, for a vector
$\mathbf {v}_S = (v_x, v_y, v_z) \in \mathbb {N}_+^3$
normal to S, we have
$m (S) \geqslant m (S)_x = \frac {l_S}{v_x}$
, where
$l_S$
is the
$\mathbf {v}_S$
-degree of
$g_S$
(also
$\mathbf {v}_S$
-order of g).
We omit elementary proofs of the following three facts on proximity faces (stated for the axis
$0 x$
for simplicity; analogous statements hold for the other axes).
Lemma 5.5 Let S be a proximate face for the axis
$0x$
, convenient with respect to this axis. If S has a diagonal joining some monomials of the form
$x^k z$
,
$k \geqslant 1$
, and
$x^m y^n$
,
$m \geqslant 0, n \geqslant 1$
, then S is the unique proximity face for the axis
$0x$
.
Lemma 5.6 Let S be a proximate face for the axis
$0 x$
. Then the supporting plane of S has the highest coordinate of intersection with the axis
$0 x$
among all the
$0 x$
-non-exceptional faces.
Lemma 5.7 Let S be a proximate face for the axis
$0x$
. Then no edges of S have prolongations intersecting the axis
$0 x$
, except, perhaps, those having at least one vertex in one of the planes
$0 x y$
,
$0 x z$
.
6 Existence of parametrizations for a proximity face
Here, we indicate a way to extend the main result of Section 4 also to the case of “zero mixed volume,” but only for proximity faces (as their geometry is “good,” in the sense of Theorem 4.5). Although one cannot claim now that there always exists a parametrization of the type postulated in Theorem 4.1, it turns out that, nevertheless, there exists a parametrization of a branch of the polar curve
$\{ \frac {\partial f}{\partial y} = 0, \frac {\partial f}{\partial z} = 0\}$
whose initial exponent vector supports a certain, rather special, subface of the chosen
$0 x$
-proximate face. Precisely, we have the following theorem.
Theorem 6.1 Let
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
be an isolated singularity, and let S be its proximity face for
$0x.$
Assume, moreover, that
$\operatorname {supp} f=\Gamma ^0 (f)$
and f has generic coefficients. Then there exists a parametrization
$\Phi = (\varphi _1, \varphi _2, \varphi _3) \in \mathbb {C} \{t\}^3$
with
$\Phi (0)=0$
and
$\varphi _1 \neq 0$
, such that
$$ \begin{align}\frac{\partial f}{\partial y}\circ\Phi=\frac{\partial f}{\partial z}\circ\Phi = 0 \end{align} $$
and its initial exponent vector is supporting either along S or along an edge of S lying in one of the planes
$0x y$
,
$0x z$
, or along the vertex of S on the axis
$0x$
.
Remark. Naturally, if
$\varphi _i=0$
, then the ith coordinate of the initial exponent vector
$\mathbf {v}$
of
$\Phi $
is understood to be equal to
$+\infty $
. For convenience, we also define
$l_{\mathbf {v}}$
,
$S_{\mathbf {v}}$
,
$\Pi _{\mathbf {v}}$
for such vectors, in a natural way, using the usual conventions for calculations involving infinity. Equivalently, one may replace the infinite coordinates of
$\mathbf {v}$
by a big enough
$N \in \mathbb {N}$
to get the vector
$\tilde {\mathbf {v}} \in \mathbb {Q}^3$
; then,
$l_{\mathbf {v}}=l_{\tilde {\mathbf {v}}}$
,
$S_{\mathbf {v}}=S_{\tilde {\mathbf {v}}}$
,
$\Pi _{\mathbf {v}} = \Pi _{\tilde {\mathbf {v}}}$
.
Proof We split the proof into two main parts, cases to be treated separately.
Part I
S is
$0x$
-non-convenient. We consider two subcases:
-
a)
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})> 0$
.Here, by Lemma 5.7, we may apply Theorem 4.5 to find a parametrization
$0 \neq \Phi \in \mathbb {C} \{t\}^3$
satisfying (6.1), whose initial exponent vector is perpendicular to S so it supports
$\Gamma _+(f)$
along S. -
b)
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z}) = 0$
.
In this situation, by Lemma 3.2,
$\mathcal {N} (\frac {\partial \overline {f_S}}{\partial y})$
and
$\mathcal {N} (\frac {\partial \overline {f_S}}{\partial z})$
are either parallel segments or at least one of these polygons reduces to a point. This implies certain restrictions on the geometry of S. First, since a derivative can zero at most two vertices of S, such S cannot have more than four vertices. But “four vertices” implies that in the derivatives
$\frac {\partial f_S}{\partial y}$
,
$\frac {\partial f_S}{\partial z}$
there are segments at the least; and if this happens, these segments either lie in different coordinate planes (if S is non-convenient for
$0 x$
) or they are derived from a common vertex of S (if S is convenient for
$0 x$
); in either case, neither they nor their projections can be parallel. This means S has to be a triangle.
Since S is a non-convenient proximity face, the triangle S has an edge joining the monomials
$x^k{}z$
, where
$k \geqslant 1$
, and
$x^m y^n$
, where
$m \geqslant 0$
,
$n \geqslant 1$
(up to permutation of the variables y and z [recall Figure 3b]).
We claim that the last vertex of S lies in the plane
$0 x z$
. Indeed, it cannot lie in
$0 x y$
for S is
$0x$
-non-exceptional; and if it were situated outside of both planes
$0 x y$
and
$0 x z$
, then we would have
$\operatorname {MV} (\frac {\partial \overline {f_S}}{\partial y}, \frac {\partial \overline {f_S}}{\partial z})> 0$
. Thus,
$S =\mathcal {N} (x^m y^n + x^k z + x^p z^q)$
. As S is
$0x$
-non-exceptional,
$n \geqslant 2$
. Moreover,
$q \geqslant 1$
since S is non-convenient with respect to
$0 x$
. Hence, we get
$p < k$
and
$q \geqslant 2$
.
We may, thus, write
$\frac {\partial f_S}{\partial y} = ax^m y^{n - 1}$
and
$\frac {\partial f_S}{\partial z} = bx^k + cx^p z^{q - 1}$
, where
$abc \neq 0$
, and
$$\begin{align*}\frac{\partial f}{\partial z} (x, 0, z) = bx^k + cx^p z^{q - 1} + \cdots. \end{align*}$$
We will show that there exists the sought
$\Phi $
with the property that its initial exponent vector supports
$\Gamma _+(f)$
along the edge of S lying in plane
$0x z$
. To this end, let
$\mathbf {w} = (w_x, w_y, w_z) \in \mathbb {N}_+^3$
be a supporting vector of
$\Gamma _+(f)$
along the edge of S joining
$x^k z$
and
$x^p z^q$
. To find such a vector
$\mathbf {w}$
, it is enough to start from a vector perpendicular to S and then increase its second coordinate (i.e., the one corresponding to y). If this increase is small enough, then we may additionally assume that
$(\frac {\partial f}{\partial y})_{\mathbf {w}} = a x^m y^{n-1}$
. Thus,
$$\begin{align*}\left (\frac{\partial f}{\partial y} \right )_{\mathbf{w}} = a x^m y^{n-1}, \quad \left ( \frac{\partial f}{\partial z}\right )_{\mathbf{w}} = bx^k + cx^p z^{q - 1}.\end{align*}$$
Letting
$w_y \rightarrow \infty $
(and keeping
$w_x$
and
$w_z$
fixed), we may arrive at two cases.
First, if
$\frac {\partial f}{\partial y} (x, 0, z) \mathrel {\not \equiv } 0$
, then, since
$n \geqslant 2$
, there exists a weight vector
$\tilde {\mathbf {w}} = (w_x, \tilde {w}_y, w_z)$
with
$\tilde {w}_y> w_y$
, for which
$(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}} = ax^m y^{n - 1} + dx^r y^s z^t + ( {\textit {other possible terms, of}}\ y {\textit {-degree}}\ {\textit {less than }} n - 1 )$
, where
$d \neq 0$
and
$s < n - 1$
. This restriction on the supported terms follows from the fact that any monomial from
$\operatorname {supp} (\frac {\partial f}{\partial y})$
with y-degree
$\geqslant n - 1$
is of weighted
$\tilde {\mathbf {w}}$
-degree higher than the
$\tilde {\mathbf {w}}$
-degree of
$x^m y^{n - 1}$
, just as was the case with the
$\mathbf {w}$
-degree. On the other hand, we still have
$(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}} = bx^k + cx^p z^{q - 1}$
. Consequently, as
$s \neq n - 1$
, if
$\mathcal {N} ((\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}})$
happens to be just the segment
$\mathcal {N} (x^m y^{n - 1} + x^r y^s z^t)$
, then the projected segments
$\mathcal {N} \left ( \overline {(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}} \right )$
and
$\mathcal {N} \left ( \overline {(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}} \right )$
are not parallel and, hence, have positive mixed volume. Clearly, the same holds if
$\mathcal {N} ((\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}})$
is a polygon. Moreover, the pair of polynomials
$\left ( \overline {(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}}, \overline {(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}} \right )$
is
$\mathcal {B}$
-nondegenerate because their coefficients originate from different vertices of
$\Gamma (f)$
and, as such, may be considered generic.
By Bernstein theorem, the system
$\left \{ \overline {(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}} = \overline {(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}} = 0 \right \}$
has
$\operatorname {MV} \left ( \overline {(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}}, \overline {(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}} \right ) > 0$
solutions in
$(\mathbb {C}^{\ast })^2$
. Hence,
$\left \{ (\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}} = (\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}} = 0 \right \}$
possesses solutions in
$(\mathbb {C}^{\ast })^3$
. This means that in the ideal
$((\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}, (\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}) \mathcal {O}_3$
there are no monomials. What is more, using—again—the relative genericness of coefficients of the polynomials
$(\frac {\partial f}{\partial y})_{\tilde {\mathbf {w}}}$
,
$(\frac {\partial f}{\partial z})_{\tilde {\mathbf {w}}}$
, we infer that these polynomials do not have any common factor except, possibly, a monomial. Consequently, Lemma 4.3 implies there is no element
$H \in (\frac {\partial f}{\partial y}, \frac {\partial f}{\partial z}) \mathcal {O}_3$
such that
$H_{\tilde {\mathbf {w}}}$
is a monomial. Thus, we may apply Maurer theorem (Theorem 3.4) to find a parametrization
$\Phi (t) = (\varphi _1 (t), \varphi _2 (t), \varphi _3 (t))$
of the curve
$\{ \frac {\partial f^{^{^{}}}}{\partial y} = \frac {\partial f}{\partial z} = 0\}$
whose initial exponent vector is a multiple of
$\tilde {\mathbf {w}}$
(hence,
$\varphi _1 \neq 0$
). But, by its construction,
$\tilde {\mathbf {w}}$
supports
$\Gamma _+(f)$
along the edge of S lying in plane
$0xz$
.
Second, if
$\frac {\partial f}{\partial y} (x, 0, z) \equiv 0$
, then let
$\Psi (t) = (\psi _1 (t), \psi _2 (t))$
be a parametrization of a branch of the curve
$\{ \frac {\partial f}{\partial z} (x, 0, z) = 0\}$
corresponding to the edge
$T := \mathcal {N} (x^k + x^p z^{q - 1})$
of its Newton polyhedron
$\Gamma _+ (\frac {\partial f}{\partial z} (x, 0, z))$
in
$\mathbb {C}^2$
. Put
$\Phi (t) = (\psi _1 (t), 0, \psi _2 (t))$
. Then
$\psi _1(t) \neq 0$
and the initial exponent vector of
$\Phi $
supports
$\Gamma _+(f)$
along the edge of S lying in plane
$0xz$
. This ends the proof of subcase b).
Part II
S is
$0x$
-convenient. In this case, we search for
$\Phi $
whose initial exponent vector supports
$\Gamma _+(f)$
along a subface of S having
$x^k$
as a vertex. We will analyze the behavior of the series
$f^{\ast } := f - e x^k$
,
$e \neq 0$
, that arises from f by removing the monomial
$x^k$
from its support.
First, let
$f^{\ast }$
be non-isolated. If
$f^{\ast }$
is not nearly convenient with respect to
$0x$
, then we put
$\Phi = (t,0,0)$
and its initial exponent vector
$(1,+\infty ,+\infty )$
supports
$\Gamma _+(f)$
along the vertex
$x^k$
. Otherwise, there exists a vertex realizing the nearly convenience, say
$x^lz$
, where
$l \geqslant 1$
. But then, from Proposition 3.5, we infer that necessarily
$\Gamma _+(f^{\ast })\cap 0xy = \varnothing $
. We shall indicate the suitable
$\Phi $
in the form
$\Phi =(\varphi _1,\varphi _2,0)$
. Clearly,
$\varphi _3=0$
already gives
$\frac {\partial f}{\partial y}\circ \Phi = 0$
. Now, we shall choose
$(\varphi _1,\varphi _2)$
for which
$\frac {\partial f}{\partial z}\circ \Phi = 0$
. From the above analysis, it follows that we may write
$f(x,y,z)=zg(x,y) + z^2h(x,y,z) + e x^k$
, where
$g(0,0)=0$
. Thus,
$\frac {\partial f}{\partial z}\circ \Phi = g(\varphi _1,\varphi _2)$
. But
$g(x,y) =\theta _1 x^l +\theta _2 y^m +\ldots $
, where
$\theta _1, \theta _2 \neq 0$
,
$m \geqslant 1$
, because f is nearly convenient with respect to the axis
$0y$
. By the Newton–Puiseux theorem, we may find
$(\varphi _1,\varphi _2)$
with
$\varphi _1 \neq 0$
,
$\varphi _1(0)=\varphi _2(0)=0$
and
$g(\varphi _1,\varphi _2)=0$
. Then
$\frac {\partial f}{\partial z}\circ \Phi = 0$
and the initial exponent vector
$(\mathrm {ord}\, \varphi _1,\mathrm {ord}\, \varphi _2,+\infty )$
of
$\Phi $
supports
$\Gamma _+(f)$
along the vertex
$x^k$
.
Now, let
$f^{\ast }$
be an isolated singularity. Suppose that
$\Gamma ^2 (f^{\ast })\backslash E_x(f^{\ast }) = \varnothing $
. Then, using Proposition 5.3, we infer that
$f^{\ast }$
has an edge
$\mathcal {N}(x^{}y + z^{\alpha })$
(up to permutation of
$(y,z)$
only), for some
$\alpha \geqslant 2$
, and
$E_x(f^{\ast })=E(f^{\ast })$
. Hence, this edge is also an edge of a non-compact, parallel to
$0y$
, face of
$f^{\ast }$
. Therefore, it is an edge of f, too, and
$\varnothing \neq E_x(f)=E(f)$
. Then, again by Proposition 5.3, we get there is no
$0x$
-non-exceptional face of f, a contradiction. Hence,
$\Gamma ^2 (f^{\ast })\backslash E_x(f^{\ast }) \neq \varnothing $
. By Proposition 5.2, there exists an
$0x$
-proximate face T of
$f^{\ast }$
, non-convenient with respect to this axis. Clearly, we are in the position to apply Part I of the proof to
$f^{\ast }$
and T. This way, we find a parametrization satisfying (6.1) such that its initial exponent vector
$\mathbf {v}$
supports
$\Gamma _+(f^{\ast })$
along N, where either
$N=T$
or N is an edge of T lying in one of the planes
$0xy$
,
$0xz$
. Take the supporting plane
$\Pi =\Pi _{\mathbf {v}}$
of
$\Gamma _+ (f^{\ast })$
along N. If
$x^k$
lies above
$\Pi $
, then
$x^k$
also lies above the plane spanned by T (because the affine hulls of T and N both intersect
$0 x$
in the same single point); thus, T happens to be an
$0 x$
-proximate face of f. But then, by Lemma 5.5, T is the unique
$0 x$
-proximate face of f so
$S=T$
. As S is
$0x$
-convenient while T is not, this is a contradiction.
Hence,
$x^k$
lies on
$\Pi $
or under it. If
$x^k$
lies on
$\Pi $
and
$N=T$
, then, by Lemma 5.5, we get that T and
$x^k$
make the unique
$0 x$
-proximate face of f. Therefore,
$\operatorname {conv} (T \cup x^k) = S$
and, by Part I of the proof, the vector
$\mathbf {v}$
supports
$\Gamma _+(f)$
along S in this case. If
$x^k$
lies on
$\Pi $
and N were an edge of T lying in one of the planes
$0xy$
or
$0xz$
, then N and
$x^k$
would make an edge of f containing three points of
$\operatorname {supp} f$
; contradiction with the assumption
$\operatorname {supp} f = \Gamma ^0(f)$
. Finally, if
$x^k$
lies under
$\Pi $
, then
$\mathbf {v}$
supports
$\Gamma _+(f)$
along the vertex
$x^k$
.
7 Proof of the main theorem
Let, as in Theorem 2.1,
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
be an isolated,
$\mathcal {K}\!$
-nondegenerate singularity,
$\Gamma (f)$
—its Newton boundary, and
$\Gamma ^2 (f) \backslash E (f) \neq \varnothing $
. Recall that the set of
$\mathcal {K}\!$
-nondegenerate holomorphic functions with a given finite support is non-empty and Zariski open in the space of coefficients of the support (cf. [Reference Kuo and LuKou76, Reference OkaOka79]); in particular, any such function with support equal to
$\Gamma ^0 (f)$
is, by Proposition 3.5, an isolated singularity (and has the same Newton boundary,
$\Gamma (f)$
). This, together with Theorem 3.1, allows us to assume that
$\operatorname {supp} f = \Gamma ^0 (f)$
and the coefficients of f are generic (for the monomials in
$\operatorname {supp} f$
). In particular, f is a polynomial. Thus, we may and will assume in the sequel that
$f : (\mathbb {C}^3, 0) \rightarrow (\mathbb {C}, 0)$
satisfies the following conditions:
-
(i) f is an isolated singularity,
-
(ii) f is
$\mathcal {K}\!$
-nondegenerate, -
(iii)
$\Gamma ^2 (f)\backslash E(f) \neq \varnothing $
, -
(iv)
$\operatorname {supp} f = \Gamma ^0 (f)$
, -
(v) the coefficients of f are generic.
We want to prove the equality
$$ \begin{align} \mathcal{L}_0 (f) = \max_{S \in \Gamma^2 (f) \backslash E (f)} m (S) - 1. \end{align} $$
Denote by
$m (f)$
the maximum on the right-hand side of the above formula. The inequality
$\mathcal {L}_0 (f) \leqslant m (f) - 1$
was established by the third-named author in [Reference OleksikOle13]. We will prove the inverse inequality,
$\mathcal {L}_0 (f) \geqslant m (f) - 1$
.
From formula (1.1), to justify this inequality, it suffices to find an analytic path
$0 \neq \Phi (t) = (\varphi _1 (t), \varphi _2 (t), \varphi _3 (t)) : (\mathbb {C}, 0) \rightarrow (\mathbb {C}^3, 0)$
for which
$$ \begin{align} \frac{\operatorname{ord} (\nabla f \circ \Phi)}{\operatorname{ord} \Phi} \geqslant m (f) - 1. \end{align} $$
By restriction (iii), every proximity face of f is non-exceptional (see Proposition 5.2). Hence, by Lemma 5.6,
$m (f)=\max \left (m(T)_{\omega }\right )$
, where T runs through the set of the faces proximate for the axes
$0 \omega $
,
$\omega \in \{ x, y, z \}$
. Fix any proximity face S; say, it is proximate for the axis
$0 x$
.
Because of the reductions (iv) and (v) made above, we can use Theorem 6.1 to get a suitable
$\Phi $
for
$S.$
Let us call its initial exponent vector
$\mathbf {v}$
, with coordinates
$(v_x, v_y, v_z) \in (\mathbb {N}_+ \cup \{+\infty \})^3$
. We have
$\varphi _1 \neq 0$
so
$v_x=\operatorname {ord} \varphi _1 \neq +\infty $
. What is more,
$\mathbf {v}$
supports
$\Gamma _+(f)$
along a subface of S whose affine hull intersects the axis
$0 x$
. Hence,
$m (S)_x = \frac {l}{v_x}$
, where
$l=l_{\mathbf {v}}$
is the
$\mathbf {v}$
-order of f. As f is
$\mathcal {K}\!$
-nondegenerate, we get
$\operatorname {ord} ( \frac {\partial f}{\partial x} \circ \Phi ) = \operatorname {ord} (f \circ \Phi ) - \operatorname {ord} \varphi _1$
. Using these observations, we can write
$$ \begin{align*} \mathcal{L}_0 (f) \geqslant \frac{\operatorname{ord} (\nabla f \circ \Phi)}{\operatorname{ord} \Phi} = \frac{\operatorname{ord} \left( \frac{\partial f}{\partial x} \circ \Phi \right)}{\operatorname{ord} \Phi} \geqslant \frac{\operatorname{ord} (f \circ \Phi) - \operatorname{ord} \varphi_1}{\operatorname{ord} \varphi_1} &\geqslant \frac{l}{v_x} - 1 =\\ &= m (S)_x - 1. \end{align*} $$
As S was an arbitrarily fixed proximity face, we infer that
$\mathcal {L}_0 (f) \geqslant m(f)-1$
. This ends the proof of the theorem.
8 Concluding remarks
The main theorem, together with Comment (1), gives an effective method of calculation of the Łojasiewicz exponent of
$\mathcal {K}\!$
-nondegenerate surface singularities. For instance, most singularities from Arnold’s list are exactly such ones. To calculate the Łojasiewicz exponent of a
$\mathcal {K}\!$
-nondegenerate surface singularity, it suffices to detect non-exceptional faces in the Newton boundary
$\Gamma (f)$
. If we do not find any, then we get an immediate answer (see Comment (1) on page 5). If we do find some such faces, we must just compute their intersections (precisely, the intersections of the planes containing them) with the coordinate axes. It suffices, however, to compute these intersections using just one (arbitrarily chosen) proximity face for each axis (it does exist by Proposition 5.2). Namely, we have.
Corollary 8.1 Let f be a
$\mathcal {K}\!$
-nondegenerate isolated surface singularity possessing non-exceptional faces and
$S_{x},S_{y},S_{z}$
be any proximate faces for axes
$0x,0y,0z$
, respectively. Then
$$\begin{align*}\mathcal{L}(f)=\max(m(S_{x})_{x},m(S_{y})_{y},m(S_{z})_{z})-1. \end{align*}$$
In particular, if non-exceptional faces of
$\Gamma (f)$
touch all the axes, say in the points
$x^{m},y^{n},z^{k}$
, then they are obviously proximate and
$$\begin{align*}\mathcal{L}(f)=\max(m,n,k)-1. \end{align*}$$
Open access
