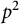1 Introduction and results
Suppose
![]() $X_1, X_2, \ldots $
are i.i.d. copies of a positive random variable and f is a nonnegative function. This article is concerned with certain combinatorial properties of the sequence
$X_1, X_2, \ldots $
are i.i.d. copies of a positive random variable and f is a nonnegative function. This article is concerned with certain combinatorial properties of the sequence
For instance,
![]() $f(x) = x^p$
is a fairly natural choice leading to the sequence of moments of averages of the
$f(x) = x^p$
is a fairly natural choice leading to the sequence of moments of averages of the
![]() $X_i$
. Because we have the identity
$X_i$
. Because we have the identity
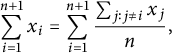 $$ \begin{align*} \sum_{i=1}^{n+1} x_i = \sum_{i=1}^{n+1}\frac{\sum_{j: j \neq i} x_j}{n}, \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n+1} x_i = \sum_{i=1}^{n+1}\frac{\sum_{j: j \neq i} x_j}{n}, \end{align*} $$
we conclude that the sequence
![]() $(a_n)_{n=1}^\infty $
is nonincreasing when f is convex. What about inequalities involving more than two terms?
$(a_n)_{n=1}^\infty $
is nonincreasing when f is convex. What about inequalities involving more than two terms?
Such inequalities have been studied to some extent. One fairly general result is due to Boland, Proschan, and Tong from [Reference Boland, Proschan, Tong, Block, Sampson and Savits1] (with applications in reliability theory). It asserts in particular that for
![]() $n = 2, 3, \ldots $
,
$n = 2, 3, \ldots $
,
for a symmetric (invariant under permuting coordinates) continuous random vector
![]() $X = (X_1,\dots ,X_{2n})$
with nonnegative components and a symmetric convex function
$X = (X_1,\dots ,X_{2n})$
with nonnegative components and a symmetric convex function
![]() $\phi : [0,+\infty )^2 \to \mathbb {R}$
.
$\phi : [0,+\infty )^2 \to \mathbb {R}$
.
We obtain a satisfactory answer to a natural question of log-convexity/concavity of sequences
![]() $(a_n)$
for completely monotone functions, also providing insights into the case of power functions.
$(a_n)$
for completely monotone functions, also providing insights into the case of power functions.
Recall that a nonnegative sequence
![]() $(x_n)_{n=1}^\infty $
supported on a set of contiguous integers is called log-convex (resp. log-concave) if
$(x_n)_{n=1}^\infty $
supported on a set of contiguous integers is called log-convex (resp. log-concave) if
![]() $x_n^2 \leq x_{n-1}x_{n+1}$
(resp.
$x_n^2 \leq x_{n-1}x_{n+1}$
(resp.
![]() $x_n^2 \geq x_{n-1}x_{n+1}$
) for all
$x_n^2 \geq x_{n-1}x_{n+1}$
) for all
![]() $n \geq 2$
(for background on log-convex/concave sequences, see, for instance, [Reference Liu and Wang8, Reference Stanley12]). One of the crucial properties of log-convex sequences is that log-convexity is preserved by taking sums (which follows from the Cauchy–Schwarz inequality, see, for instance, [Reference Liu and Wang8]). Recall that an infinitely differentiable function
$n \geq 2$
(for background on log-convex/concave sequences, see, for instance, [Reference Liu and Wang8, Reference Stanley12]). One of the crucial properties of log-convex sequences is that log-convexity is preserved by taking sums (which follows from the Cauchy–Schwarz inequality, see, for instance, [Reference Liu and Wang8]). Recall that an infinitely differentiable function
![]() $f: (0,\infty ) \to (0,\infty )$
is called completely monotone if we have
$f: (0,\infty ) \to (0,\infty )$
is called completely monotone if we have
![]() $(-1)^nf^{(n)}(x) \geq 0$
for all positive x and
$(-1)^nf^{(n)}(x) \geq 0$
for all positive x and
![]() $n = 1, 2, \ldots $
; equivalently, by Bernstein’s theorem (see, for instance, [Reference Feller7]), the function f is the Laplace transform of a nonnegative Borel measure
$n = 1, 2, \ldots $
; equivalently, by Bernstein’s theorem (see, for instance, [Reference Feller7]), the function f is the Laplace transform of a nonnegative Borel measure
![]() $\mu $
on
$\mu $
on
![]() $[0,+\infty )$
, that is,
$[0,+\infty )$
, that is,
For example, when
![]() $p<0$
, the function
$p<0$
, the function
![]() $f(x) = x^p$
is completely monotone. Such integral representations are at the heart of our first two results.
$f(x) = x^p$
is completely monotone. Such integral representations are at the heart of our first two results.
Theorem 1 Let
![]() $f\colon (0,\infty )\rightarrow (0,\infty )$
be a completely monotone function. Let
$f\colon (0,\infty )\rightarrow (0,\infty )$
be a completely monotone function. Let
![]() $X_1, X_2, \ldots $
be i.i.d. positive random variables. Then, the sequence
$X_1, X_2, \ldots $
be i.i.d. positive random variables. Then, the sequence
![]() $(a_n)_{n=1}^\infty $
defined by (1) is log-convex.
$(a_n)_{n=1}^\infty $
defined by (1) is log-convex.
Theorem 2 Let
![]() $f\colon [0,\infty )\rightarrow [0,\infty )$
be such that
$f\colon [0,\infty )\rightarrow [0,\infty )$
be such that
![]() $f(0) = 0$
and its derivative
$f(0) = 0$
and its derivative
![]() $f'$
is completely monotone. Let
$f'$
is completely monotone. Let
![]() $X_1, X_2, \ldots $
be i.i.d. nonnegative random variables. Then, the sequence
$X_1, X_2, \ldots $
be i.i.d. nonnegative random variables. Then, the sequence
![]() $(a_n)_{n=1}^\infty $
defined by (1) is log-concave.
$(a_n)_{n=1}^\infty $
defined by (1) is log-concave.
In particular, applying these to the functions
![]() $f(x) = x^p$
with
$f(x) = x^p$
with
![]() $p < 0$
and
$p < 0$
and
![]() $0 < p < 1$
, respectively, we obtain the following corollary.
$0 < p < 1$
, respectively, we obtain the following corollary.
Corollary 3 Let
![]() $X_1, X_2, \ldots $
be i.i.d. positive random variables. The sequence
$X_1, X_2, \ldots $
be i.i.d. positive random variables. The sequence
is log-convex when
![]() $p < 0$
and log-concave when
$p < 0$
and log-concave when
![]() $0 < p < 1$
.
$0 < p < 1$
.
For
![]() $p> 1$
, we pose the following conjecture.
$p> 1$
, we pose the following conjecture.
Conjecture 1 Let
![]() $p> 1$
. Let
$p> 1$
. Let
![]() $X_1, X_2, \ldots $
be i.i.d. nonnegative random variables. Then, the sequence
$X_1, X_2, \ldots $
be i.i.d. nonnegative random variables. Then, the sequence
![]() $(b_n)$
defined in (4) is log-convex.
$(b_n)$
defined in (4) is log-convex.
We offer a partial result supporting this conjecture.
Theorem 4 Let
![]() $X_1, X_2, \ldots $
be i.i.d. nonnegative random variables, let p be a positive integer, and let
$X_1, X_2, \ldots $
be i.i.d. nonnegative random variables, let p be a positive integer, and let
![]() $b_n$
be defined by (4). Then, for every
$b_n$
be defined by (4). Then, for every
![]() $n \geq p^2$
, we have
$n \geq p^2$
, we have
![]() $b_n^2 \leq b_{n-1}b_{n+1}$
.
$b_n^2 \leq b_{n-1}b_{n+1}$
.
Remark 5 When
![]() $p = 2$
, we have
$p = 2$
, we have
![]() $b_n = \frac {n\mathbb {E} X_1^2 + n(n-1)(\mathbb {E} X_1)^2}{n^2} = (\mathbb {E} X_1)^2 + n^{-1} \operatorname {\mathrm {Var}}(X_1)$
, which is clearly a log-convex sequence (as a sum of two log-convex sequences). The following argument for
$b_n = \frac {n\mathbb {E} X_1^2 + n(n-1)(\mathbb {E} X_1)^2}{n^2} = (\mathbb {E} X_1)^2 + n^{-1} \operatorname {\mathrm {Var}}(X_1)$
, which is clearly a log-convex sequence (as a sum of two log-convex sequences). The following argument for
![]() $p=3$
was kindly communicated to us by Krzysztof Oleszkiewicz: when
$p=3$
was kindly communicated to us by Krzysztof Oleszkiewicz: when
![]() $p=3$
, we can write
$p=3$
, we can write
The sequences
![]() $(n^{-2})$
and
$(n^{-2})$
and
![]() $(3n^{-1}-n^{-2})$
are log-convex. By the Cauchy–Schwarz inequality, the factor at
$(3n^{-1}-n^{-2})$
are log-convex. By the Cauchy–Schwarz inequality, the factor at
![]() $n^{-2}$
is nonnegative,
$n^{-2}$
is nonnegative,
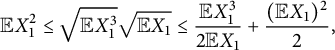 $$ \begin{align*} \mathbb{E} X_1^2 \leq \sqrt{\mathbb{E} X_1^3}\sqrt{\mathbb{E} X_1} \leq \frac{\mathbb{E} X_1^3}{2\mathbb{E} X_1} + \frac{(\mathbb{E} X_1)^2}{2}, \end{align*} $$
$$ \begin{align*} \mathbb{E} X_1^2 \leq \sqrt{\mathbb{E} X_1^3}\sqrt{\mathbb{E} X_1} \leq \frac{\mathbb{E} X_1^3}{2\mathbb{E} X_1} + \frac{(\mathbb{E} X_1)^2}{2}, \end{align*} $$
so again
![]() $(b_n)$
is log-convex as a sum of three log-convex sequences. It remains elusive how to group terms and proceed along these lines in general. Our proof of Theorem 4 relies on this idea, but uses a straightforward way of rearranging terms.
$(b_n)$
is log-convex as a sum of three log-convex sequences. It remains elusive how to group terms and proceed along these lines in general. Our proof of Theorem 4 relies on this idea, but uses a straightforward way of rearranging terms.
Remark 6 It would be tempting to use the aforementioned result of Boland et al. with
![]() $\phi (x,y) = (xy)^p$
to resolve Conjecture 1. However, this function is neither convex nor concave on
$\phi (x,y) = (xy)^p$
to resolve Conjecture 1. However, this function is neither convex nor concave on
![]() $(0,+\infty )^2$
for
$(0,+\infty )^2$
for
![]() $p> \frac {1}{2}$
. For
$p> \frac {1}{2}$
. For
![]() $0 < p < \frac {1}{2}$
, the function is concave and (2) yields
$0 < p < \frac {1}{2}$
, the function is concave and (2) yields
![]() $(b_nn^p)^2 \geq b_{n-1}(n-1)^pb_{n+1}(n+1)^p$
,
$(b_nn^p)^2 \geq b_{n-1}(n-1)^pb_{n+1}(n+1)^p$
,
![]() $n \geq 2$
, equivalently,
$n \geq 2$
, equivalently,
![]() $b_n^2 \geq \left (\frac {n^2-1}{n^2}\right )^pb_{n-1}b_{n+1}$
. Corollary 3 improves on this by removing the factor
$b_n^2 \geq \left (\frac {n^2-1}{n^2}\right )^pb_{n-1}b_{n+1}$
. Corollary 3 improves on this by removing the factor
![]() $\left (\frac {n^2-1}{n^2}\right )^p < 1$
. For
$\left (\frac {n^2-1}{n^2}\right )^p < 1$
. For
![]() $p < 0$
,
$p < 0$
,
![]() $\phi $
is convex, so (2) gives
$\phi $
is convex, so (2) gives
![]() $b_n^2 \leq \left (\frac {n^2-1}{n^2}\right )^pb_{n-1}b_{n+1}$
and Corollary 3 removes the factor
$b_n^2 \leq \left (\frac {n^2-1}{n^2}\right )^pb_{n-1}b_{n+1}$
and Corollary 3 removes the factor
![]() $\left (\frac {n^2-1}{n^2}\right )^p> 1$
.
$\left (\frac {n^2-1}{n^2}\right )^p> 1$
.
Concluding this introduction, it is of significant interest to study the log-behavior of various sequences, particularly those emerging from algebraic, combinatorial, or geometric structures, which has involved and prompted the development of many deep and interesting methods, often useful beyond the original problems (see, e.g., [Reference Brenti3–Reference Fadnavis6, Reference Nayar and Oleszkiewicz10–Reference Stanley13]). We propose to consider sequences of moments of averages of i.i.d. random variables arising naturally in probabilistic limit theorems. For moments of order less than
![]() $1$
, we employ an analytical approach exploiting integral representations for power functions. For moments of order higher than
$1$
, we employ an analytical approach exploiting integral representations for power functions. For moments of order higher than
![]() $1$
, our Conjecture 1, besides refining the monotonicity property of the sequence
$1$
, our Conjecture 1, besides refining the monotonicity property of the sequence
![]() $(b_n)$
(resulting from convexity), would furnish new examples of log-convex sequences. For instance, neither does it seem trivial, nor handled by known techniques, to determine whether the sequence, obtained by taking the Bernoulli distribution with parameter
$(b_n)$
(resulting from convexity), would furnish new examples of log-convex sequences. For instance, neither does it seem trivial, nor handled by known techniques, to determine whether the sequence, obtained by taking the Bernoulli distribution with parameter
![]() $\theta \in (0,1)$
,
$\theta \in (0,1)$
,
![]() $b_n = \sum _{k=0}^n \binom {n}{k}\left (\frac {k}{n}\right )^p\theta ^k(1-\theta )^{n-k}$
is log-convex. In the case of integral p, we have
$b_n = \sum _{k=0}^n \binom {n}{k}\left (\frac {k}{n}\right )^p\theta ^k(1-\theta )^{n-k}$
is log-convex. In the case of integral p, we have
![]() $b_n = \sum _{k=0}^p S(p,k)\frac {n!}{(n-k)!n^p}\theta ^k$
, where
$b_n = \sum _{k=0}^p S(p,k)\frac {n!}{(n-k)!n^p}\theta ^k$
, where
![]() $S(p,k)$
is the Stirling number of the second kind.
$S(p,k)$
is the Stirling number of the second kind.
The rest of this paper is occupied with the proofs of Theorems 1, 2, and 4 (in their order of statement), and then we conclude with additional remarks and conjectures.
2 Proofs
2.1 Proof of Theorem 1
Suppose that f is completely monotone. Using (3) and independence, we have
Let
![]() $u_n(t) = \left [\mathbb {E} e^{-tX_1/n}\right ]^n$
. It suffices to show that for every positive t, the sequence
$u_n(t) = \left [\mathbb {E} e^{-tX_1/n}\right ]^n$
. It suffices to show that for every positive t, the sequence
![]() $(u_n(t))$
is log-convex (because sums/integrals of log-convex sequences are log-convex: the Cauchy–Schwarz inequality applied to the measure
$(u_n(t))$
is log-convex (because sums/integrals of log-convex sequences are log-convex: the Cauchy–Schwarz inequality applied to the measure
![]() $\mu $
yields
$\mu $
yields
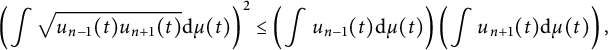 $$ \begin{align*} \left(\int \sqrt{u_{n-1}(t)u_{n+1}(t)} \mathrm{d}\mu(t)\right)^2 \leq \left(\int u_{n-1}(t) \mathrm{d}\mu(t)\right)\left(\int u_{n+1}(t) \mathrm{d}\mu(t)\right), \end{align*} $$
$$ \begin{align*} \left(\int \sqrt{u_{n-1}(t)u_{n+1}(t)} \mathrm{d}\mu(t)\right)^2 \leq \left(\int u_{n-1}(t) \mathrm{d}\mu(t)\right)\left(\int u_{n+1}(t) \mathrm{d}\mu(t)\right), \end{align*} $$
which combined with
![]() $u_n(t) \leq \sqrt {u_{n-1}(t)u_{n+1}(t)}$
, gives
$u_n(t) \leq \sqrt {u_{n-1}(t)u_{n+1}(t)}$
, gives
![]() $a_n^2 \leq a_{n-1}a_{n+1}$
). The log-convexity of
$a_n^2 \leq a_{n-1}a_{n+1}$
). The log-convexity of
![]() $(u_n(t))$
follows from Hölder’s inequality,
$(u_n(t))$
follows from Hölder’s inequality,
which finishes the proof.
2.2 Proof of Theorem 2
Suppose now that
![]() $f(0) = 0$
and
$f(0) = 0$
and
![]() $f'$
is completely monotone, say
$f'$
is completely monotone, say
![]() $f'(x) = \int _0^\infty e^{-tx}\mathrm {d}\mu (t)$
for some nonnegative Borel measure
$f'(x) = \int _0^\infty e^{-tx}\mathrm {d}\mu (t)$
for some nonnegative Borel measure
![]() $\mu $
on
$\mu $
on
![]() $(0,\infty )$
(by (3)). Introducing a new measure
$(0,\infty )$
(by (3)). Introducing a new measure
![]() $\mathrm {d}\nu (t) = \frac {1}{t}\mathrm {d}\mu (t)$
, we can write
$\mathrm {d}\nu (t) = \frac {1}{t}\mathrm {d}\mu (t)$
, we can write
Integrating against
![]() $\mathrm {d} x$
gives
$\mathrm {d} x$
gives
Let F be the Laplace transform of
![]() $X_1$
, that is,
$X_1$
, that is,
Then,
where, to shorten the notation, we introduce the following nonnegative function:
To show the inequality
it suffices to show that pointwise
for all
![]() $s, t> 0$
. This follows from two properties of the function G:
$s, t> 0$
. This follows from two properties of the function G:
-
(1) for every fixed
 $t>0$
, the function
$t>0$
, the function
 $\alpha \mapsto G(\alpha ,t)$
is nondecreasing,
$\alpha \mapsto G(\alpha ,t)$
is nondecreasing, -
(2) the function
 $G(\alpha ,t)$
is concave on
$G(\alpha ,t)$
is concave on
 $(0,\infty )\times (0,\infty )$
.
$(0,\infty )\times (0,\infty )$
.
Indeed, by (2), we have
(in fact, we only use concavity in the first argument). It thus suffices to prove that
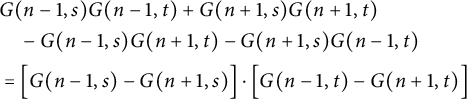 $$ \begin{align*} & G(n-1,s)G(n-1,t)+G(n+1,s)G(n+1,t) \\ &\quad- G(n-1,s)G(n+1,t) - G(n+1,s)G(n-1,t) \\ &= \Big[G(n-1,s)-G(n+1,s)\Big]\cdot \Big[G(n-1,t)-G(n+1,t)\Big] \end{align*} $$
$$ \begin{align*} & G(n-1,s)G(n-1,t)+G(n+1,s)G(n+1,t) \\ &\quad- G(n-1,s)G(n+1,t) - G(n+1,s)G(n-1,t) \\ &= \Big[G(n-1,s)-G(n+1,s)\Big]\cdot \Big[G(n-1,t)-G(n+1,t)\Big] \end{align*} $$
is nonnegative, which follows by (1).
It remains to prove (1) and (2). To prove the former, notice that
![]() $F(t/\alpha )^\alpha = \left (\mathbb {E} e^{-tX/\alpha }\right )^{\alpha } = { \|e^{-tX}\|_{1/\alpha }}$
is the
$F(t/\alpha )^\alpha = \left (\mathbb {E} e^{-tX/\alpha }\right )^{\alpha } = { \|e^{-tX}\|_{1/\alpha }}$
is the
![]() $L_{1/\alpha }$
-norm of
$L_{1/\alpha }$
-norm of
![]() $e^{-tX}$
. By convexity, for an arbitrary random variable Z,
$e^{-tX}$
. By convexity, for an arbitrary random variable Z,
![]() $p \mapsto (\mathbb {E}|Z|^p)^{1/p} = \|Z\|_p$
is nondecreasing, so
$p \mapsto (\mathbb {E}|Z|^p)^{1/p} = \|Z\|_p$
is nondecreasing, so
![]() $F(t/\alpha )^\alpha = \|e^{-tX}\|_{1/\alpha }$
is nonincreasing and thus
$F(t/\alpha )^\alpha = \|e^{-tX}\|_{1/\alpha }$
is nonincreasing and thus
![]() $G(\alpha ,t) = 1 - F(t/\alpha )^\alpha $
is nondecreasing. To prove the latter, notice that by Hölder’s inequality the function
$G(\alpha ,t) = 1 - F(t/\alpha )^\alpha $
is nondecreasing. To prove the latter, notice that by Hölder’s inequality the function
![]() $t \mapsto \log F(t)$
is convex,
$t \mapsto \log F(t)$
is convex,
Therefore, its perspective function
![]() $H(\alpha ,t) = \alpha \log F(t/\alpha )$
is convex (see, e.g., Chapter 3.2.6 in [Reference Boyd and Vandenberghe2]), which implies that
$H(\alpha ,t) = \alpha \log F(t/\alpha )$
is convex (see, e.g., Chapter 3.2.6 in [Reference Boyd and Vandenberghe2]), which implies that
![]() $F(t/\alpha )^{\alpha } = e^{H(\alpha ,t)}$
is also convex.
$F(t/\alpha )^{\alpha } = e^{H(\alpha ,t)}$
is also convex.
2.3 Proof of Theorem 4
We recall a standard combinatorial formula: first, by the multinomial theorem and independence, we have
where the sum is over all sequences
![]() $(p_1,\dots ,p_n)$
of nonnegative integers such that
$(p_1,\dots ,p_n)$
of nonnegative integers such that
![]() $p_1+\dots +p_n = p$
and we denote
$p_1+\dots +p_n = p$
and we denote
![]() $\mu _k = \mathbb {E} X_1^k$
,
$\mu _k = \mathbb {E} X_1^k$
,
![]() $k \geq 0$
. Now, we partition the summation according to the number m of positive terms in the sequence
$k \geq 0$
. Now, we partition the summation according to the number m of positive terms in the sequence
![]() $(p_1,\ldots ,p_n)$
. Let
$(p_1,\ldots ,p_n)$
. Let
![]() $Q_m$
be the set of integer partitions of p into exactly m (nonempty) parts, that is, the set of m-element multisets
$Q_m$
be the set of integer partitions of p into exactly m (nonempty) parts, that is, the set of m-element multisets
![]() $q = \{q_1,\dots , q_m\}$
with positive integers
$q = \{q_1,\dots , q_m\}$
with positive integers
![]() $q_j$
summing to p,
$q_j$
summing to p,
![]() $q_1+\dots + q_m = p$
. Then,
$q_1+\dots + q_m = p$
. Then,
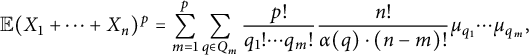 $$ \begin{align*} \mathbb{E} (X_1+\dots+X_n)^p = \sum_{m=1}^p\sum_{q \in Q_m}\frac{p!}{q_1!\cdots q_m!}\frac{n!}{\alpha(q)\cdot(n-m)!}\mu_{q_1}\cdots\mu_{q_m}, \end{align*} $$
$$ \begin{align*} \mathbb{E} (X_1+\dots+X_n)^p = \sum_{m=1}^p\sum_{q \in Q_m}\frac{p!}{q_1!\cdots q_m!}\frac{n!}{\alpha(q)\cdot(n-m)!}\mu_{q_1}\cdots\mu_{q_m}, \end{align*} $$
where
![]() $\alpha (q) = l_1!\cdots l_h!$
for
$\alpha (q) = l_1!\cdots l_h!$
for
![]() $q = \{q_1,\ldots ,q_m\}$
with exactly h distinct terms such that there are
$q = \{q_1,\ldots ,q_m\}$
with exactly h distinct terms such that there are
![]() $l_1$
terms of type
$l_1$
terms of type
![]() $1$
,
$1$
,
![]() $l_2$
terms of type
$l_2$
terms of type
![]() $2$
, etc., so
$2$
, etc., so
![]() $l_1+\dots +l_h = m$
(e.g., for
$l_1+\dots +l_h = m$
(e.g., for
![]() $q = \{2,2,2,3,4,4\} \in Q_6$
, we have
$q = \{2,2,2,3,4,4\} \in Q_6$
, we have
![]() $h=3$
,
$h=3$
,
![]() $l_1 = 3$
,
$l_1 = 3$
,
![]() $l_2 = 1$
, and
$l_2 = 1$
, and
![]() $l_3=2$
). The factor
$l_3=2$
). The factor
![]() $\frac {n!}{\alpha (q)\cdot (n-m)!}$
arises, because given a multiset
$\frac {n!}{\alpha (q)\cdot (n-m)!}$
arises, because given a multiset
![]() $q \in Q_m$
, there are exactly
$q \in Q_m$
, there are exactly
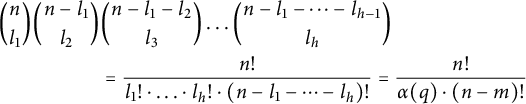 $$ \begin{align*} \binom{n}{l_1}\binom{n-l_1}{l_2}&\binom{n-l_1-l_2}{l_3}\dots\binom{n-l_1-\dots-l_{h-1}}{l_h} \\ &= \frac{n!}{l_1!\cdot\ldots\cdot l_h!\cdot (n-l_1-\cdots-l_h)!} = \frac{n!}{\alpha(q)\cdot (n-m)!} \end{align*} $$
$$ \begin{align*} \binom{n}{l_1}\binom{n-l_1}{l_2}&\binom{n-l_1-l_2}{l_3}\dots\binom{n-l_1-\dots-l_{h-1}}{l_h} \\ &= \frac{n!}{l_1!\cdot\ldots\cdot l_h!\cdot (n-l_1-\cdots-l_h)!} = \frac{n!}{\alpha(q)\cdot (n-m)!} \end{align*} $$
many nonnegative integer-valued sequences
![]() $(p_1,\ldots ,p_n)$
such that
$(p_1,\ldots ,p_n)$
such that
![]() $\mu _{p_1}\cdots \mu _{p_n} = \mu _{q_1}\cdots \mu _{q_m}$
(equivalently,
$\mu _{p_1}\cdots \mu _{p_n} = \mu _{q_1}\cdots \mu _{q_m}$
(equivalently,
![]() $\{p_1,\ldots ,p_n\} = \{q_1,\ldots ,q_m,0\}$
, as sets).
$\{p_1,\ldots ,p_n\} = \{q_1,\ldots ,q_m,0\}$
, as sets).
We have obtained
 $$ \begin{align} b_n = \mathbb{E} \left(\frac{X_1+\dots+X_n}{n}\right)^p = \sum_{m=1}^p \frac{n!}{n^p(n-m)!} \sum_{q \in Q_m}\beta(q){ \mu(q)}, \end{align} $$
$$ \begin{align} b_n = \mathbb{E} \left(\frac{X_1+\dots+X_n}{n}\right)^p = \sum_{m=1}^p \frac{n!}{n^p(n-m)!} \sum_{q \in Q_m}\beta(q){ \mu(q)}, \end{align} $$
where
![]() $\beta (q) = \frac {p!}{\alpha (q)\cdot q_1!\cdots q_m!}$
and
$\beta (q) = \frac {p!}{\alpha (q)\cdot q_1!\cdots q_m!}$
and
![]() $\mu (q) = \mu _{q_1}\cdots \mu _{q_m}$
. By homogeneity, we can assume that
$\mu (q) = \mu _{q_1}\cdots \mu _{q_m}$
. By homogeneity, we can assume that
![]() $\mu _1 = \mathbb {E} X_1 = 1$
. Note that when
$\mu _1 = \mathbb {E} X_1 = 1$
. Note that when
![]() $X_1$
is constant, we get from (5) that
$X_1$
is constant, we get from (5) that
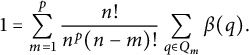 $$ \begin{align*} 1 = \sum_{m=1}^p \frac{n!}{n^p(n-m)!} \sum_{q \in Q_m}\beta(q). \end{align*} $$
$$ \begin{align*} 1 = \sum_{m=1}^p \frac{n!}{n^p(n-m)!} \sum_{q \in Q_m}\beta(q). \end{align*} $$
Because
![]() $Q_p$
has only one element, namely
$Q_p$
has only one element, namely
![]() $\{1,\ldots ,1\}$
and
$\{1,\ldots ,1\}$
and
![]() $\mu (\{1,\ldots ,1\}) = 1$
, when we subtract the two equations, the terms corresponding to
$\mu (\{1,\ldots ,1\}) = 1$
, when we subtract the two equations, the terms corresponding to
![]() $m=p$
cancel and we get
$m=p$
cancel and we get
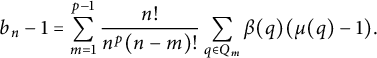 $$ \begin{align*} b_n - 1 = \sum_{m=1}^{p-1} \frac{n!}{n^p(n-m)!}\sum_{q \in Q_m} \beta(q)(\mu(q)-1). \end{align*} $$
$$ \begin{align*} b_n - 1 = \sum_{m=1}^{p-1} \frac{n!}{n^p(n-m)!}\sum_{q \in Q_m} \beta(q)(\mu(q)-1). \end{align*} $$
By the monotonicity of moments,
![]() $\mu (q) \geq 1$
for every q, so
$\mu (q) \geq 1$
for every q, so
![]() $(b_n)$
is a sum of the constant sequence
$(b_n)$
is a sum of the constant sequence
![]() $(1,1,\ldots )$
and the sequences
$(1,1,\ldots )$
and the sequences
![]() $(u_n^{(m)}) = (\frac {n!}{n^p(n-m)!})$
,
$(u_n^{(m)}) = (\frac {n!}{n^p(n-m)!})$
,
![]() $m=1,\ldots ,p-1$
, multiplied, respectively, by the nonnegative factors
$m=1,\ldots ,p-1$
, multiplied, respectively, by the nonnegative factors
![]() $\sum _{q \in Q_m} \beta (q)(\mu (q)-1)$
. Because sums of log-convex sequences are log-convex, it remains to verify that for each
$\sum _{q \in Q_m} \beta (q)(\mu (q)-1)$
. Because sums of log-convex sequences are log-convex, it remains to verify that for each
![]() $1 \leq m \leq p-1$
, we have
$1 \leq m \leq p-1$
, we have
![]() $(u_n^{(m)})^2 \leq u_{n-1}^{(m)}u_{n+1}^{(m)}$
,
$(u_n^{(m)})^2 \leq u_{n-1}^{(m)}u_{n+1}^{(m)}$
,
![]() $n \geq p^2$
. The following lemma finishes the proof.
$n \geq p^2$
. The following lemma finishes the proof.
Lemma 7 Let
![]() $p \geq 2$
,
$p \geq 2$
,
![]() $1 \leq m \leq p-1$
, be integers. Then, the function
$1 \leq m \leq p-1$
, be integers. Then, the function
is convex on
![]() $[p^2-1,\infty )$
.
$[p^2-1,\infty )$
.
Proof The statement is clear for
![]() $m=1$
. Let
$m=1$
. Let
![]() $2 \leq m \leq p-1$
and
$2 \leq m \leq p-1$
and
![]() $p \geq 3$
. We have
$p \geq 3$
. We have
 $$ \begin{align*} x^2f''(x) = p-1 - x^2\sum_{k=1}^{m-1} \frac{1}{(x-k)^2}. \end{align*} $$
$$ \begin{align*} x^2f''(x) = p-1 - x^2\sum_{k=1}^{m-1} \frac{1}{(x-k)^2}. \end{align*} $$
To see that this is positive for every
![]() $x \geq p^2-1$
and
$x \geq p^2-1$
and
![]() $2 \leq m \leq p-1$
, it suffices to consider
$2 \leq m \leq p-1$
, it suffices to consider
![]() $m = p-1$
and
$m = p-1$
and
![]() $x = p^2-1$
(writing
$x = p^2-1$
(writing
![]() $\frac {x}{x-k} = 1 + \frac {k}{x-k}$
, we see that the right-hand side is increasing in x). Because
$\frac {x}{x-k} = 1 + \frac {k}{x-k}$
, we see that the right-hand side is increasing in x). Because
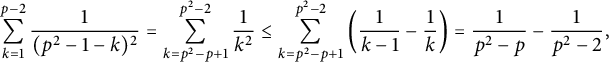 $$ \begin{align*} \sum_{k=1}^{p-2} \frac{1}{(p^2-1-k)^2} = \sum_{k=p^2-p+1}^{p^2-2} \frac{1}{k^2} \leq \sum_{k=p^2-p+1}^{p^2-2} \left(\frac{1}{k-1} - \frac{1}{k}\right) &= \frac{1}{p^2-p} - \frac{1}{p^2-2}, \end{align*} $$
$$ \begin{align*} \sum_{k=1}^{p-2} \frac{1}{(p^2-1-k)^2} = \sum_{k=p^2-p+1}^{p^2-2} \frac{1}{k^2} \leq \sum_{k=p^2-p+1}^{p^2-2} \left(\frac{1}{k-1} - \frac{1}{k}\right) &= \frac{1}{p^2-p} - \frac{1}{p^2-2}, \end{align*} $$
we have
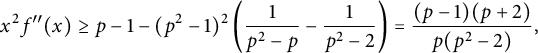 $$ \begin{align*} x^2f''(x) \geq p-1-(p^2-1)^2\left(\frac{1}{p^2-p} - \frac{1}{p^2-2}\right) = \frac{(p-1)(p+2)}{p(p^2-2)}, \end{align*} $$
$$ \begin{align*} x^2f''(x) \geq p-1-(p^2-1)^2\left(\frac{1}{p^2-p} - \frac{1}{p^2-2}\right) = \frac{(p-1)(p+2)}{p(p^2-2)}, \end{align*} $$
which is clearly positive. □
3 Final remarks
Remark 8 Using majorization-type arguments (see, e.g., [Reference Marshall, Olkin and Arnold9]), Conjecture 1 can be verified in a rather standard but lengthy way for every
![]() $p>1$
and
$p>1$
and
![]() $n=2$
. The idea is to establish a pointwise inequality: we conjecture that for nonnegative numbers
$n=2$
. The idea is to establish a pointwise inequality: we conjecture that for nonnegative numbers
![]() $x_1,\ldots ,x_{2n}$
and a convex function
$x_1,\ldots ,x_{2n}$
and a convex function
![]() $\phi : [0,\infty )\to [0,\infty )$
, we have
$\phi : [0,\infty )\to [0,\infty )$
, we have
 $$ \begin{align*} \frac{1}{\binom{2n}{n}}\sum_{|I|=n}\phi\left(\frac{x_Ix_{I^c}}{n^2}\right) \leq \frac{1}{\binom{2n}{n+1}}\sum_{|I|=n+1}\phi\left(\frac{x_Ix_{I^c}}{n^2-1}\right),\end{align*} $$
$$ \begin{align*} \frac{1}{\binom{2n}{n}}\sum_{|I|=n}\phi\left(\frac{x_Ix_{I^c}}{n^2}\right) \leq \frac{1}{\binom{2n}{n+1}}\sum_{|I|=n+1}\phi\left(\frac{x_Ix_{I^c}}{n^2-1}\right),\end{align*} $$
where for a subset I of the set
![]() $\{1,\ldots ,2n\}$
, we denote
$\{1,\ldots ,2n\}$
, we denote
![]() $x_I = \sum _{i\in I} x_i$
. We checked that this holds for
$x_I = \sum _{i\in I} x_i$
. We checked that this holds for
![]() $n=2$
. Taking the expectation on both sides for
$n=2$
. Taking the expectation on both sides for
![]() $\phi (x) = x^p$
gives the desired result that
$\phi (x) = x^p$
gives the desired result that
![]() $b_n^2 \leq b_{n-1}b_{n+1}$
.
$b_n^2 \leq b_{n-1}b_{n+1}$
.
Remark 9 It is tempting to ask for generalizations of Conjecture 1 beyond the power functions, say to ask whether the sequence
![]() $(a_n)$
defined in (1) is log-convex for every convex function f. This is false, as can be seen by taking the function f of the form
$(a_n)$
defined in (1) is log-convex for every convex function f. This is false, as can be seen by taking the function f of the form
![]() $f(x) = \max \{x-a,0\}$
and the
$f(x) = \max \{x-a,0\}$
and the
![]() $X_i$
to be i.i.d. Bernoulli random variables.
$X_i$
to be i.i.d. Bernoulli random variables.
Acknowledgment
We would like to thank Krzysztof Oleszkiewicz for his great help, valuable correspondence, feedback, and for allowing us to use his slick proof for
![]() $p=3$
from Remark 5. We would also like to thank Marta Strzelecka and Michał Strzelecki for the helpful discussions. We are indebted to the referees for their careful reading and useful comments. We are grateful for the excellent working conditions provided by the Summer Undergraduate Research Fellowship 2019 at Carnegie Mellon University during which this work was initiated.
$p=3$
from Remark 5. We would also like to thank Marta Strzelecka and Michał Strzelecki for the helpful discussions. We are indebted to the referees for their careful reading and useful comments. We are grateful for the excellent working conditions provided by the Summer Undergraduate Research Fellowship 2019 at Carnegie Mellon University during which this work was initiated.