Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T19:02:22.269Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Heuristics and an Exact Formula for Abelian Surfaces Over Finite Fields

Published online by Cambridge University Press:  20 November 2018

Jeffrey Achter  and
Cassandra Williams
Jeffrey Achter
Affiliation:
Colorado State University, Fort Collins, CO 80523-1874, USA e-mail: [email protected]
Cassandra Williams
Affiliation:
James Madison University, Harrisonburg, VA 22807, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

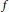Consider a quartic $q$-Weil polynomial $f$. Motivated by equidistribution considerations, we define, for each prime 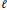$\ell$, a local factor that measures the relative frequency with which 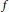$f$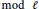$ \bmod \,\ell $ occurs as the characteristic polynomial of a symplectic similitude over 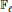${{\mathbb{F}}_{\ell }}$. For a certain class of polynomials, we show that the resulting infinite product calculates the number of principally polarized abelian surfaces over 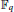${{\mathbb{F}}_{q}}$ with Weil polynomial 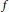$f$.

Keywords

14K02abelian surfacesfinite fieldsrandom matrices
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 4 , 01 December 2015 , pp. 673 - 691
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Breeding, J. II, Irreducible characters of GSp(4, q) and dimensions of spaces of fixed vectors. Ramanujan J. 36(2015), no. 3, 305–354. http://dx.doi.Org/10.1007/s11139-014-9622-3 Google Scholar
[2] Broker, R., Gruenewald, D., and Lauter, K., Explicit CM theory for level 2-structures on abelian surfaces. Algebra Number Theory 5(2011), no. 4, 495–528. http://dx.doi.Org/10.2140/ant.2011.5.495 Google Scholar
[3] Carter, R. W., Finite groups of Lie type. Wiley Classics Library John Wiley & Sons Ltd., Chichester, 1993.Google Scholar
[4] Fulman, J., A probabilistic approach to conjugacy classes in the finite symplectic and orthogonal groups. J. Algebra 234(2000), no. 1, 207–224. http://dx.doi.Org/10.1OO6/jabr.2000.8455 Google Scholar
[5] Gekeler, E.-U., Frobenius distributions of elliptic curves over finite prime fields. Int. Math. Res. Not. 37(2003), 1999–2018.Google Scholar
[6] Goren, E. Z. and Lauter, K. E., Genus 2 curves with complex multiplication. Int. Math. Res. Not. IMRN 5(2012), 1068–1142.Google Scholar
[7] Howe, E. W, Principally polarized ordinary abelian varieties over finite fields. Trans. Amer. Math. Soc. 347(1995), no. 7, 2361–2401. http://dx.doi.Org/10.2307/2154828 Google Scholar
[8] Katz, N. M., Lang-Trotter revisited. Bull. Amer. Math. Soc. (N.S.) 46,(2009), no. 3, 413–457. http://dx.doi.Org/10.1090/S0273-0979-09-01257-9 Google Scholar
[9] Shinoda, K.-i., The characters of the finite conformai symplectic group, CSp(4, q). Comm. Algebra 10(1982), no. 13, 1369–1419. http://dx.doi.Org/10.1080/00927878208822782 Google Scholar
[10] Wall, G. E., On the conjugacy classes in the unitary, symplectic and orthogonal groups. J. Austral. Math. Soc. 3(1963), 1–62. http://dx.doi.Org/10.1017/S1446788700027622 Google Scholar
[11] Weyl, H., The classical groups. Princeton Landmarks in Mathematics, Princeton University Press, Princeton, NJ, 1997.Google Scholar