Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T09:22:11.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Littlewood–Paley Characterizations of Second-Order Sobolev Spaces via Averages on Balls

Published online by Cambridge University Press:  20 November 2018

Ziyi He ,
Dachun Yang  and
Wen Yuan
Ziyi He
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s Republic of China e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Dachun Yang
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s Republic of China e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Wen Yuan
Affiliation:
School of Mathematical Sciences, Beijing Normal University, Laboratory of Mathematics and Complex Systems, Ministry of Education, Beijing 100875, People’s Republic of China e-mail: [email protected] e-mail: [email protected] e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, the authors characterize second-order Sobolev spaces 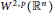${{W}^{2,p}}({{\mathbb{R}}^{n}})$ , with 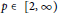$p\,\in \,[2,\,\infty )$ and 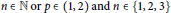$n\,\in \,\mathbb{N}\,\text{or}\,p\,\in \,(1,\,2)\,\text{and}\,n\,\in \,\left\{ 1,\,2,\,3 \right\}$ , via the Lusin area function and the Littlewood–Paley 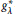$g_{\text{ }\!\!\lambda\!\!\text{ }}^{*}$ -function in terms of ball means.

Keywords

46E3542B2542B2042B35Sobolev spaceball meansLusin-area functiong*λ-function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 1 , 01 March 2016 , pp. 104 - 118
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Alabern, R., Mateu, J.. and Verdera, J.. A new characterization ofSobolev spaces on R”. Math. Ann. 354(2012), 589–626. http://dx.doi.Org/10.1007/s00208-011-0738-0 Google Scholar
[2] Coifman, R. R., Meyer, Y.. and Stein, E. M., Some new function spaces and their applications to harmonic analysis. J. Funct. Anal. 62(1985), 304–335. http://dx.doi.Org/10.1016/0022-1236(85)90007-2 Google Scholar
[3] Dai, F., Gogatishvili, A.. Yang, D.. and Yuan, W.. Characterizations ofSobolev spaces via averages on balls. Nonlinear Anal., to appear. http://dx.doi.Org/10.1016/j.na.2O15.07.024 Google Scholar
[4] Dai, F., Gogatishvili, A.. Yang, D.. and Yuan, W., Characterizations ofBesov and Triebel-Lizorkin spaces via averages on balls. arxiv:1507.08004v1Google Scholar
[5] Fefferman, C. and Stein, E. M., Some maximal inequalities. Amer. J. Math. 93(1971), 107–115. http://dx.doi.Org/10.2307/2373450 Google Scholar
[6] Garcia-Cuerva, J. and Rubio de Francia, J. L., Weighted norm inequalities and related topics. North-Holland Mathematics Studies, 116, North-Holland Publishing Co., Amsterdam, 1985.Google Scholar
[7] Hajlasz, P., Sobolev spaces on an arbitrary metric space. Potential Anal. 5(1996), 403–415.Google Scholar
[8] Heinonen, J., Koskela, P.. Shanmugalingam, N.. and Tyson, J.. Sobolev spaces on metric measure spaces: an approach based on upper gradients. New Mathematical Monographs, Cambridge University Press, Cambridge, 2015.Google Scholar
[9] Shanmugalingam, N., Newtonian spaces: an extension ofSobolev spaces to metric measure spaces. Rev. Mat. Iberoamericana 16(2000), 243–279. http://dx.doi.Org/10.4171/RMI/275 Google Scholar
[10] Stein, E. M., Singular integrals and differentiability properties of functions. Princeton Mathematical Series, 30, Princeton University Press, Princeton, NJ, 1970.Google Scholar
[11] Torchinsky, A., Real-variable methods in harmonic analysis. Pure and Applied Mathematics, 123, Academic Press, Inc., Orlando, FL, 1986.Google Scholar
[12] Ullrich, T., Continuous characterizations of Besov-Lizorkin-Triebel spaces and new interpretations as coorbits. J. Funct. Spaces Appl. 2012, Art. ID 163213, 47 pp. http://dx.doi.Org/!0.1155/2012/163213 Google Scholar