Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T18:28:02.299Z Has data issue: false hasContentIssue false
  • English
  • Français

Linéarisation symplectique en dimension 2

Published online by Cambridge University Press:  20 November 2018

Carlos Currás-Bosch
Carlos Currás-Bosch*
Affiliation:
Departament d’Algebra i Geometria, DGICYT PB96-1178 Universitat de Barcelona Gran Via 585 08007 Barcelona Spain, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper the germ of neighborhood of a compact leaf in a Lagrangian foliation is symplectically classified when the compact leaf is 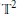${{\mathbb{T}}^{2}}$, the affine structure induced by the Lagrangian foliation on the leaf is complete, and the holonomy of 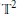${{\mathbb{T}}^{2}}$ in the foliation linearizes. The germ of neighborhood is classified by a function, depending on one transverse coordinate, this function is related to the affine structure of the nearly compact leaves.

Keywords

53C1258F05symplectic manifoldLagrangian foliationaffine connection
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 2 , 01 June 2001 , pp. 129 - 139
Copyright
Copyright © Canadian Mathematical Society 2001

References

Références

[1] Currás-Bosch, C., Sur les feuilletages Lagrangiens `a holonomie linéaire. C. R. Acad. Sci. Paris 317 (1993), 605–608.Google Scholar
[2] Currás-Bosch, C. et Molino, P., Voisinage d’une feuille compacte dans un feuilletage Lagrangien: le problème de linéarisation symplectique. Hokkaido Math. J. 23 (1994), 355–360.Google Scholar
[3] Currás-Bosch, C. et Molino, P., Réduction symplectique d’un feuilletage Lagrangien au voisinage d’une feuille compacte. C. R. Acad. Sci. Paris 318 (1994), 661–664.Google Scholar
[4] Currás-Bosch, C. et Molino, P., Un exemple de classification de germes de feuilletages Lagrangiens au voisinage d’une feuille compacte. Indag.Math. (N.S.) (2) 19 (1998), 197–209.Google Scholar
[5] Dazord, P., Sur la géométrie des sous-fibrés et des feuilletages Lagrangiens. Ann. Sci. École Norm. Sup. 4 14 (1981), 465–480.Google Scholar
[6] Kuiper, N. H., Sur les surfaces localement affines. Colloque de Géométrie Différentielle (Strasbourg, 1953), Centre National de la Recherche Scientifique, Paris, 1953, 79–87.Google Scholar
[7] Libermann, P. et Marle, Ch. M., Symplectic Geometry and Analytical Mechanics. D. Reidel Publishing Company, 1987.Google Scholar
[8] Molino, P., Exposés au Séminaire Sud-Rhodanien. Avignon, 1990, et Marseille, 1990.Google Scholar
[9] Nagano, T. et Yagi, K., The affine structures on the real two torus. Osaka J. Math. 11 (1974), 181–210.Google Scholar
[10] Weinstein, A., Lectures on symplectic manifolds. Regional Conference Series in Mathematics 29, Amer. Math. Soc., Providence, RI, 1977.Google Scholar
[11] Weinstein, A., Symplectic manifolds and their Lagrangian submanifolds. Adv. Math. 6 (1971), 329–346.Google Scholar