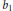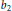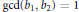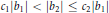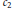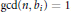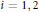Let ${{b}_{1}}$, ${{b}_{2}}$ be any integers such that $\gcd \left( {{b}_{1}},{{b}_{2}} \right)=1$ and ${{c}_{1}}\left| {{b}_{1}} \right|\,<\,\left| {{b}_{2}} \right|\,\le \,{{c}_{2}}\left| {{b}_{1}} \right|$ , where ${{c}_{1}}$, ${{c}_{2}}$ are any given positive constants. Let $n$ be any integer satisfying $\gcd \left( n,\,{{b}_{i}} \right)\,=\,1$ , $i\,=\,1,\,2$. Let 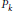${{P}_{k}}$ denote any integer with no more than $k$ prime factors, counted according to multiplicity. In this paper, for almost all 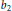${{b}_{2}}$ , we prove (i) a sharp lower bound for $n$ such that the equation 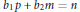${{b}_{1}}p\,+\,{{b}_{2}}m\,=\,n$ is solvable in prime 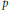$p$ and almost prime 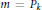$m\,=\,{{P}_{k}}$ , 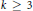$k\,\ge \,3$ whenever both 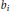${{b}_{i}}$ are positive, and (ii) a sharp upper bound for the least solutions 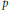$p$, 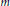$m$ of the above equation whenever 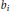${{b}_{i}}$ are not of the same sign, where 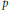$p$ is a prime and 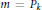$m\,=\,{{P}_{k}}$ , 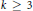$k\,\ge \,3$.