Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lynch, S.
1995.
Limit cycles of generalized Liénard equations.
Applied Mathematics Letters,
Vol. 8,
Issue. 6,
p.
15.
Lynch, S.
1997.
Liénard systems and the second part of Hilbert's sixteenth problem.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 30,
Issue. 3,
p.
1395.
Llibre, J.
and
Makhlouf, A.
2015.
Limit Cycles of a Class of Generalized Liénard Polynomial Equations.
Journal of Dynamical and Control Systems,
Vol. 21,
Issue. 2,
p.
189.
Li, Shimin
and
Wu, Kuilin
2016.
On the Limit Cycles Bifurcating from Piecewise Quasi-Homogeneous Differential Center.
International Journal of Bifurcation and Chaos,
Vol. 26,
Issue. 07,
p.
1650116.


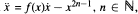 with
with 