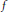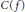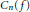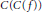Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Maya, David
Ordoñez, Norberto
and
Sánchez-Martínez, Javier
2017.
Induced mappings on hyperspaces C(p,X) and K(X).
Topology and its Applications,
Vol. 232,
Issue. ,
p.
222.
Maya, David
Pellicer-Covarrubias, Patricia
and
Pichardo-Mendoza, Roberto
2017.
Induced mappings on the hyperspace of convergent sequences.
Topology and its Applications,
Vol. 229,
Issue. ,
p.
85.
Macías, Sergio
2018.
Topics on Continua.
p.
371.