Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T10:02:47.358Z Has data issue: false hasContentIssue false
  • English
  • Français

Lie Powers and Pseudo-Idempotents

Published online by Cambridge University Press:  20 November 2018

Marianne Johnson  and
Ralph Stöhr
Marianne Johnson
Affiliation:
School of Mathematics, University of Manchester, Manchester, M13 9PL, U.K.e-mail: [email protected]@manchester.ac.uk
Ralph Stöhr
Affiliation:
School of Mathematics, University of Manchester, Manchester, M13 9PL, U.K.e-mail: [email protected]@manchester.ac.uk
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a new factorisation of the classical Dynkin operator, an element of the integral group ring of the symmetric group that facilitates projections of tensor powers onto Lie powers. As an application we show that the iterated Lie power 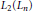${{L}_{2}}({{L}_{n}})$ is a module direct summand of the Lie power 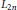${{L}_{2n}}$ whenever the characteristic of the ground field does not divide $n$. An explicit projection of the latter onto the former is exhibited in this case.

Keywords

17B0120C30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 2 , 01 June 2011 , pp. 297 - 301
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Bryant, R. M., Lie powers of infinite-dimensional modules. Beiträge Algebra Geom. 50(2009), no. 1, 179–193.Google Scholar
[2] Bryant, R. M. and Schocker, M., The decomposition of Lie powers. Proc. London Math. Soc. (3) 93(2006), no. 1, 175–196. doi:10.1017/S0024611505015728Google Scholar
[3] Erdmann, K. and Schocker, M., Modular Lie powers and the Solomon descent algebra. Math. Z. 253(2006), no. 2, 295–313. doi:10.1007/s00209-005-0901-yGoogle Scholar
[4] Magnus, W., Karras, A., and Solitar, D., Combinatorial group theory: Presentations of groups in terms of generators and relations. Wiley-Interscience, New York, 1966.Google Scholar
[5] Reutenauer, C., Free Lie algebras. London Mathematical Society Monographs, New Series, 7, The Clarendon Press, Oxford University Press, New York, 1993.Google Scholar