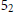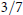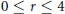Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
TRAN, Anh T.
2015.
On left-orderability and cyclic branched coverings.
Journal of the Mathematical Society of Japan,
Vol. 67,
Issue. 3,
TRAN, Anh T.
2015.
On left-orderable fundamental groups and Dehn surgeries on knots.
Journal of the Mathematical Society of Japan,
Vol. 67,
Issue. 1,
Khan, Arafat
and
Tran, Anh T.
2021.
Classical pretzel knots and left orderability.
International Journal of Mathematics,
Vol. 32,
Issue. 11,
TRAN, Anh T.
2021.
Left orderable surgeries of double twist knots.
Journal of the Mathematical Society of Japan,
Vol. 73,
Issue. 3,
The Khoi, Vu
Teragaito, Masakazu
and
Tran, Anh T.
2021.
Left orderable surgeries of double twist knots II.
Canadian Mathematical Bulletin,
Vol. 64,
Issue. 3,
p.
624.
Gao, Xinghua
2022.
Slope of orderable Dehn filling of two-bridge knots.
Journal of Knot Theory and Its Ramifications,
Vol. 31,
Issue. 01,