No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
Let
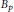 ${{B}_{p}}$
be the unit ball in
${{B}_{p}}$
be the unit ball in
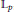 ${{\mathbb{L}}_{p}}$
,
${{\mathbb{L}}_{p}}$
, 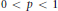 $0\,<\,p\,<\,1$, and let
$0\,<\,p\,<\,1$, and let
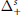 $\Delta _{+}^{s}$
,
$\Delta _{+}^{s}$
, 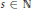 $s\,\in \,\mathbb{N}$, be the set of all
$s\,\in \,\mathbb{N}$, be the set of all  $s$-monotone functions on a finite interval
$s$-monotone functions on a finite interval  $I$, i.e.,
$I$, i.e.,
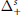 $\Delta _{+}^{s}$
consists of all functions
$\Delta _{+}^{s}$
consists of all functions 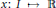 $x\,:\,I\,\mapsto \,\mathbb{R}$ such that the divided differences
$x\,:\,I\,\mapsto \,\mathbb{R}$ such that the divided differences
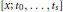 $[x;\,{{t}_{0}},\,...\,,\,{{t}_{s}}]$
of order
$[x;\,{{t}_{0}},\,...\,,\,{{t}_{s}}]$
of order  $s$ are nonnegative for all choices of
$s$ are nonnegative for all choices of 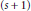 $\left( s\,+\,1 \right)$ distinct points
$\left( s\,+\,1 \right)$ distinct points
 ${{t}_{0}},\,.\,.\,.\,,{{t}_{s}}\,\in \,I.$ For the classes
${{t}_{0}},\,.\,.\,.\,,{{t}_{s}}\,\in \,I.$ For the classes
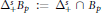 $\Delta _{+}^{s}{{B}_{P}}\,:=\,\Delta _{+}^{s}\,\cap \,{{B}_{P}},$ we obtain exact orders of Kolmogorov, linear and pseudo-dimensional widths in the spaces
$\Delta _{+}^{s}{{B}_{P}}\,:=\,\Delta _{+}^{s}\,\cap \,{{B}_{P}},$ we obtain exact orders of Kolmogorov, linear and pseudo-dimensional widths in the spaces
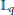 ${{\mathbb{L}}_{q}},$
${{\mathbb{L}}_{q}},$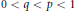 $0\,<\,q\,<\,p\,<\,1$:
$0\,<\,q\,<\,p\,<\,1$:
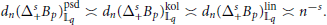 $${{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{psd}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{kol}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{lin}}\asymp {{n}^{-s}}.$$
$${{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{psd}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{kol}}\asymp {{d}_{n}}(\Delta _{+}^{s}{{B}_{P}})_{{{\mathbb{L}}_{q}}}^{\text{lin}}\asymp {{n}^{-s}}.$$