Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:14:52.968Z Has data issue: false hasContentIssue false
  • English
  • Français

The Kernel of 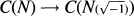and the 4-Rank of K2(O)

Published online by Cambridge University Press:  20 November 2018

Ruth I. Berger
Ruth I. Berger*
Affiliation:
Department of Mathematical Sciences Memphis State University Memphis, Tennessee 38152 U. S. A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

An upper bound is given for the order of the kernel of the map on Sideal class groups that is induced by 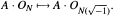For some special types of number fields F the connection between the size of the above kernel for 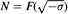and the units and norms in 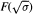are examined. Let K2(O) denote the Milnor K-group of the ring of integers of a number field. In some cases a formula by Conner, Hurrelbrink and Kolster is extended to show how closely the 4-rank of 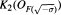is related to the 4-rank of the S-ideal class group of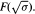

Keywords

11R19
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 35 , Issue 3 , 01 September 1992 , pp. 295 - 302
Copyright
Copyright © Canadian Mathematical Society 1992

References

1. Berger, R.L, Quadratic extensions with elementary abelian K2(0), J. Algebra 142(1991), 394–404.Google Scholar
2. Conner, RE. and Hurrelbrink, J., Class number parity , Pure Math. Series 8, World Scientific Publishing Co., Singapore, 1988.Google Scholar
3. Conner, RE. and Hurrelbrink, J., The 4-Rank of K2(0), Can. J. of Math., Vol XLI, No. 5 (1989), 932–960.Google Scholar
4. Gras, G., Remarks on K2 of number fields , J. Number Th. 23 (1986), No. 3, 322–335.Google Scholar
5. Gras, G. and Jaulent, J.F., Sur les corps de nombres réguliers, Math. Z. 202 (1989), 343–365.Google Scholar
6. Kolster, M., The structure of the 2-Sylow-subgroupofK2(0)I, Comm. Math. Helv. 61 (1986), 376–388.Google Scholar
7. Tate, J., Relations between K2 and Galois cohomology, Invent. math. 36 (1976), 257–274.Google Scholar