Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T13:51:16.393Z Has data issue: false hasContentIssue false
  • English
  • Français

Jordan–Chevalley Decomposition in Lie Algebras

Part of: Lie algebras and Lie superalgebras Nonassociative rings and algebras Representation theory of groups Basic linear algebra

Published online by Cambridge University Press:  28 February 2019

Leandro Cagliero  and
Fernando Szechtman
Leandro Cagliero
Affiliation:
CIEM-CONICET, FAMAF-Universidad Nacional de Córdoba, Córdoba, Argentina Email: [email protected]
Fernando Szechtman
Affiliation:
Department of Mathematics and Statistics, Univeristy of Regina, Regina, SK Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if $\mathfrak{s}$ is a solvable Lie algebra of matrices over a field of characteristic 0 and 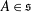$A\in \mathfrak{s}$, then the semisimple and nilpotent summands of the Jordan–Chevalley decomposition of 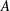$A$ belong to $\mathfrak{s}$ if and only if there exist 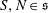$S,N\in \mathfrak{s}$, 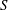$S$ is semisimple, 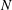$N$ is nilpotent (not necessarily 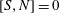$[S,N]=0$) such that 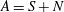$A=S+N$.

Keywords

solvable Lie algebraJordan–Chevalley decompositionrepresentation

MSC classification

Primary: 17-08: Computational methods
Secondary: 17B05: Structure theory 20C40: Computational methods 15A21: Canonical forms, reductions, classification
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 349 - 354
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author L. C. was supported in part by CONICET and SECYT-UNC grants.

Author F. S. was supported in part by an NSERC discovery grant.

References

Bourbaki, N., Lie Groups and Lie Algebras: chapters 1–3. Springer-Verlag, Berlin, 1989.Google Scholar
Bourbaki, N., Lie Groups and Lie Algebras: chapters 7–9. Springer-Verlag, Berlin, 2005.Google Scholar
Cagliero, L. and Szechtman, F., Jordan–Chevalley decomposition in finite dimensional Lie algebras . Proc. Amer. Math. Soc. 139(2011), no. 11, 3909–3913. https://doi.org/10.1090/S0002-9939-2011-10827-X.Google Scholar
Cagliero, L. and Szechtman, F., The classification of uniserial $\mathfrak{s}\mathfrak{l}(2)\rtimes V(m)$ -modules and a new interpretation of the Racah–Wigner 6j-symbol. J. Algebra 386(2013), 142–175. https://doi.org/10.1016/j.jalgebra.2013.03.022.Google Scholar
Cagliero, L. and Szechtman, F., On the theorem of the primitive element with applications to the representation theory of associative and Lie Algebras . Canad. Math. Bull. 57(2014), no. 4, 735–748. https://doi.org/10.4153/CMB-2013-046-9.Google Scholar
Fulton, W. and Harris, J., Representation theory: A first course. Graduate Texts in Mathematics, 129, Readings in Mathematics, Springer-Verlag, New York, 1991. https://doi.org/10.1007/978-1-4612-0979-9.Google Scholar
Hoffman, K. and Kunze, R., Linear algebra. Second ed., Prentice-Hall, New Jersey, 1971.Google Scholar
Humphreys, J. E., Introduction to Lie algebras and representation theory. Graduate Texts in Mathematics, 9, Springer-Verlag, New York-Berlin, 1978.Google Scholar
Kim, K.-T., Criteria for the existence of a Jordan–Chevalley-Seligman decomposition . J. Algebra 424(2015), 376–389. https://doi.org/10.1016/j.jalgebra.2014.09.028.Google Scholar