Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-23T06:51:25.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Jeśmanowicz’ Conjecture with Congruence Relations. II

Published online by Cambridge University Press:  20 November 2018

Yasutsugu Fujita  and
Takafumi Miyazaki
Yasutsugu Fujita
Affiliation:
Department of Mathematics, College of Industrial Technology, Nihon University, 2-11-1 Shin-ei, Narashino, Chiba, Japan e-mail: [email protected]
Takafumi Miyazaki
Affiliation:
Department of Mathematics, College of Science and Technology, Nihon University 1-8-14 Kanda-Surugadai, Chiyoda-ku, Tokyo 101-8308, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $a$, 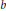$b$, and $c$ be primitive Pythagorean numbers such that 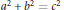${{a}^{2}}\,+\,{{b}^{2}}\,=\,{{c}^{2}}$ with 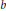$b$ even. In this paper, we show that if 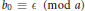${{b}_{0}}\,\equiv \,\in \,\,\,\left( \bmod \,a \right)$ with 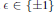$\text{ }\!\!\varepsilon\!\!\text{ }\,\in \,\left\{ \pm 1 \right\}$ for certain positive divisors 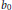${{b}_{0}}$ of 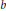$b$, then the Diophantine equation 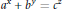${{a}^{x}}\,+\,{{b}^{y}}\,=\,{{c}^{z}}$ has only the positive solution 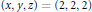$\left( x,\,y,\,z \right)\,=\,\left( 2,\,2,\,2 \right)$.

Keywords

11D6111D09exponential Diophantine equationsPythagorean triplesPell equations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 3 , 01 September 2014 , pp. 495 - 505
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Dem’janenko, V. A., On Jeśmanowicz’ problem for Pythagorean numbers. (Russian) Izv. Vyssh. Ucebn. Zaved. Matematika 1965, no. 5 (48), 52–56.Google Scholar
[2] Deng, M. and Cohen, G. L., A note on a conjecture of Jeśmanowicz. Colloq. Math. 86 (2000), no. 1, 25–30.Google Scholar
[3] Fujita, Y., The non-extensibility of D(4k)-triples {1; 4k(k – 1); 4k. + 1g with |k| prime. Glas. Mat. Ser. III 41 (61) (2006), no. 2, 205–216. http://dx.doi.org/10.3336/gm.41.2.03 Google Scholar
[4] Fujita, Y. and Miyazaki, T., Jeśmanowicz’ conjecture with congruence relations. Colloq. Math. 128 (2012), no. 2, 211–222. http://dx.doi.org/10.4064/cm128-2-6 Google Scholar
[5] Jeśmanowicz, L., Several remarks on Pythagorean numbers. (Polish)Wiadom. Mat. 1(1955/1956), 196–202.Google Scholar
[6] Laurent, M., Linear forms in two logarithms and interpolation determinants II. Acta Arith. 133 (2008), no. 4, 325–348. http://dx.doi.org/10.4064/aa133-4-3 Google Scholar
[7] Lu, W. T., On the Pythagorean numbers 4n2-1, 4n and 4n2 + 1. (Chinese) Acta Sci. Natur. Univ. Szechuan 2 (1959), 39–42.Google Scholar
[8] Miyazaki, T., Jeśmanowicz’ conjecture on exponential Diophantine equations. Funct. Approx. Comment. Math. 45 (2011), part 2, 207–229. http://dx.doi.org/10.7169/facm/1323705814 Google Scholar
[9] Miyazaki, T., Generalizations of classical results on Jeśmanowicz’ conjecture concerning Pythagorean triples. J. Number Theory 133 (2013), no. 2, 583–595. http://dx.doi.org/10.1016/j.jnt.2012.08.018 Google Scholar
[10] Sierpiński, W., On the equation 3x + 4y . 5 z .(Polish)Wiadom. Mat. 1(1955/1956), 194–195.Google Scholar