Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-22T05:34:12.717Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphisms and Automorphisms of Witt Rings

Published online by Cambridge University Press:  20 November 2018

David Leep  and
Murray Marshall
David Leep
Affiliation:
University of Kentucky, LexingtonKY, 40506
Murray Marshall
Affiliation:
University of Saskatchewan, SaskatoonSASK., S7N 0W0
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

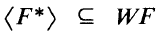For a field F, char(F) ≠ 2, let WF denote the Witt ring of quadratic forms of F and let denote the multiplicative group of 1-dimensional forms 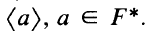It follows from a construction of D. K. Harrison that if 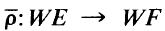E, F are fields (both of characteristic ≠ 2) and ρ.WE → WF is a ring isomorphism, then there exists a ring isomorphism which “preserves dimension” in the sense that 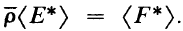In this paper, the relationship between ρ and 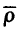is clarified.

Keywords

10C0510C03
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 2 , 01 June 1988 , pp. 250 - 256
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Arason, J. and Pfister, A., Beweis des Krullschen Durchschnittsatzes fur der Wittring, Invent. Math. 12(1971), pp. 173–176.Google Scholar
2. Cordes, C. M., The Witt group and equivalence of fields with respect to quadratic forms, J. Algebra 26 (1973), pp. 400–421.Google Scholar
3. Harrison, D. K., Witt rings, lecture notes, Department of Mathematics, University of Kentucky, Lexington (1970).Google Scholar
4. Lam, T. Y., The algebraic theory of quadratic forms, Benjamin, New York (1973).Google Scholar
5. Marshall, M., Exponentials and logarithms on Witt rings, Pac. J. of Math. 127 (1) (1987), pp. 127–140.Google Scholar
6. Marshall, M., Abstract Witt Rings, Queen's Papers in Pure and Applied Math. 57, Queen's University, Kingston, Ontario (1980).Google Scholar
7. Marshall, M. and Yucas, J., Linked quaternionic mappings and their associated Witt rings, Pac. J. of Math. 95 (2) (1981), pp. 411–425.Google Scholar