Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T18:47:49.930Z Has data issue: false hasContentIssue false
  • English
  • Français

Isomorphism Classes of Solenoidal Algebras I

Published online by Cambridge University Press:  20 November 2018

Berndt Brenken
Berndt Brenken*
Affiliation:
Department of Mathematics University of Calgary Calgary, Alberta T2N 1N4
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Each g ∊ ℤ[x] defines a homeomorphism of a compact space 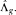We investigate the isomorphism classes of the C*-crossed product algebra Bg associated with the dynamical system 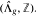An isomorphism invariant Eg of the algebra Bg is shown to determine the algebra Bg up to * or * anti-isomorphism if degree g ≤ 1 and 1 is not a root of g or if degree g = 2 and g is irreducible. It is also observed that the entropy of the dynamical system 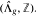is equal to the growth rate of the periodic points if g has no roots of unity as zeros. This slightly extends the previously known equality of these two quantities under the assumption that g has no zeros on the unit circle.

Keywords

46L3528D20
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 36 , Issue 4 , 01 December 1993 , pp. 414 - 418
Copyright
Copyright © Canadian Mathematical Society 1993

References

1. Brenken, B. and Jorgensen, P., A family of dilation crossed product algebras, J. Operator Theory 25(1991), 299–308.Google Scholar
2. Kitchens, B. and Schmidt, K., Automorphisms of compact groups, Ergod. Th. and Dynam. Sys. 9(1989), 691–735.Google Scholar
3. Kawamura, S., Tomiyama, J. and Watatani, Y., Finite dimensional irreducible representations ofC* -algebras associated with topological dynamical systems, Math. Scand. 56(1985), 241–248.Google Scholar
4. Lawton, W., The structure of compact connected groups which admit an expansive automorphism, Springer Lecture Notes in Math. 318(1973), 182–196.Google Scholar
5. Lind, D., Schmidt, K. and Ward, T., Mahler Measure and Entropy for Commuting Automorphisms of Compact Groups, Invent. Math. (3) 101(1990), 593–629.Google Scholar
6. Lind, D. and Ward, T., Automorphisms of solenoids andp-adic entropy, Ergod. Th. and Dynam. Sys. 8( 1988), 411–419.Google Scholar