Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Adams, Robert A.
1970.
Equivalent norms for Sobolev spaces.
Proceedings of the American Mathematical Society,
Vol. 24,
Issue. 1,
p.
63.


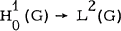 is valid if G is the "spiny urchin" domain obtained by removing from the plane the union of the sets S
is valid if G is the "spiny urchin" domain obtained by removing from the plane the union of the sets S