Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-19T09:01:47.708Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducible Tuples Without the Boundary Property

Published online by Cambridge University Press:  20 November 2018

Sameer Chavan
Sameer Chavan*
Affiliation:
Indian Institute of Technology Kanpur, Kanpur- 208016, India. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine spectral behavior of irreducible tuples that do not admit the boundary property. In particular, we prove under some mild assumption that the spectral radius of such an $m$-tuple 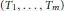$\left( {{T}_{1}},\,.\,.\,.\,,\,{{T}_{m}} \right)$must be the operator norm of 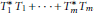$T_{1}^{*}\,{{T}_{1}}\,+\,.\,.\,.\,+\,T_{m}^{*}{{T}_{m}}$. We use this simple observation to ensure the boundary property for an irreducible, essentially normal, joint q-isometry, provided it is not a joint isometry. We further exhibit a family of reproducing Hilbert 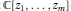$\mathbb{C}\left[ {{z}_{1}},\,.\,.\,.\,,{{z}_{m}} \right]$-modules (of which the Drury–Arveson Hilbert module is a prototype) with the property that any two nested unitarily equivalent submodules are indeed equal.

Keywords

47A1346E22boundary representationssubnormaljoint p-isometry
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 1 , 01 March 2015 , pp. 9 - 18
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Arveson, W., Subalgebras of C*-algebras II. Acta Math. 128 (1972), no. 3–4. 271–308. http://dx.doi.org/10.1007/BF02392166 Google Scholar
[2] Arveson, W., An invitation to C*-algebras. Graduate Texts in Mathematics, 39, Springer, New York, 1976.Google Scholar
[3] Arveson, W., Subalgebras of C*-algebras. III. Multivariable operator theory. Acta Math. 181 (1998), no. 2, 159–228. http://dx.doi.org/10.1007/BF02392585 Google Scholar
[4] Athavale, A., On the intertwining of joint isometries. J. Operator Theory 23 (1990), no. 2, 339–350. Google Scholar
[5] Athavale, A., Model theory on the unit ball in Cn. J. Operator Theory 27 (1992), no. 2, 347–358. Google Scholar
[6] Chavan, S. and Curto, R., Operators Cauchy dual to 2-hyperexpansive operators: the multivariable case. Integral Equations Operator Theory 73 (2012), no. 4, 481–516. http://dx.doi.org/10.1007/s00020-012-1986-4 Google Scholar
[7] Chavan, S. and Sholapurkar, V. M., Rigidity theorems for spherical hyperexpansions. Complex Anal. Oper. Theory 7 (2013), no. 5, 1545–1568. http://dx.doi.org/10.1007/s11785-012-0270-6 Google Scholar
[8] Chavan, S. and Yakubovich, D., Spherical tuples of Hilbert space operators. Indiana Univ. Math. J., to appear.Google Scholar
[9] Cho, M. and Zelazko, W., On geometric spectral radius of commuting n-tuples of operators. Hokkaido Math. J. 21 (1992), 251-258. http://dx.doi.org/10.14492/hokmj/1381413680 Google Scholar
[10] Curto, R., Applications of several complex variables to multiparameter spectral theory. Surveys of some recent results in operator theory. Volume II, Pitman Res. Notes Math. Ser., 192, Longman Sci. Tech., Harlow, 1988, pp. 25–90..Google Scholar
[11] Curto, R. and Salinas, N., Spectral properties of cyclic subnormal m-tuples. Amer. J.Math. 107 (1985), no. 1, 113–138. http://dx.doi.org/10.2307/2374459 Google Scholar
[12] Gleason, J. and Richter, S., m-isometric commuting tuples of operators on a Hilbert space. Integral Equations Operator Theory 56 (2006), no. 2, 181–196. http://dx.doi.org/10.1007/s00020-006-1424-6 Google Scholar
[13] Greene, D. C. V., S. Richter, and C. Sundberg, The structure of inner multipliers on spaces with complete Nevanlinna-Pick kernels. J. Funct. Anal. 194 (2002), no. 2, 311–331. http://dx.doi.org/10.1006/jfan.2002.3928 Google Scholar
[14] Guo, K., Hu, J., and Xu, X., Toeplitz algebras, subnormal tuples and rigidity on reproducing C[z1, … zd]-modules. J. Funct. Anal. 210 (2004), no. 1, 214–247. http://dx.doi.org/10.1016/j.jfa.2003.06.003 Google Scholar
[15] Müller, V. and Soltysiak, A., Spectral radius formula for commuting Hilbert space operators. Studia Math. 103 (1992), no. 3, 329–333. Google Scholar
[16] Putinar, M., Spectral inclusion for subnormal n-tuples. Proc. Amer. Math. Soc. 90 (1984), no. 3, 405–406. Google Scholar