Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T14:23:36.542Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducible Polynomials Over a Finite Field with Restricted Coefficients

Part of: Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  07 January 2019

Sam Porritt
Sam Porritt*
Affiliation:
Department of Mathematics, University College London, London, England Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

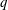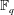We prove a function field analogue of Maynard’s celebrated result about primes with restricted digits. That is, for certain ranges of parameters $n$ and $q$, we prove an asymptotic formula for the number of irreducible polynomials of degree $n$ over a finite field $\mathbb{F}_{q}$ whose coefficients are restricted to lie in a given subset of 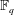$\mathbb{F}_{q}$.

Keywords

finite fieldirreducible polynomialrestricted coefficients

MSC classification

Primary: 11T55: Arithmetic theory of polynomial rings over finite fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 429 - 439
Copyright
© Canadian Mathematical Society 2018 

Footnotes

This work was supported by the Engineering and Physical Sciences Research Council EP/L015234/1 via the EPSRC Centre for Doctoral Training in Geometry and Number Theory (The London School of Geometry and Number Theory), University College London.

References

Dartyge, C., Mauduit, C., and Sárközy, A., Polynomial values and generators with missing digits in finite fields . Funct. Approx. Comment. Math. 52(2015), 65–74. https://doi.org/10.7169/facm/2015.52.1.5.Google Scholar
Dietmann, R., Elsholtz, C., and Shparlinski, I., Prescribing the binary digits of squarefree numbers and quadratic residues . Trans. Amer. Math. Soc. 369(2017), 8369–8388. https://doi.org/10.1090/tran/6903.Google Scholar
Ha, J., Irreducible polynomials with several prescribed coefficients . Finite Field Appl. 40(2016), 10–25. https://doi.org/10.1016/j.ffa.2016.02.006.Google Scholar
Hayes, D. R., The expression of a polynomial as a sum of three irreducibles . Acta Arith. 11(1966), 461–488. https://doi.org/10.4064/aa-11-4-461-488.Google Scholar
Maynard, J., Primes with restricted digits. 2016. arxiv:1604.01041.Google Scholar
Oppenheim, A. and Shusterman, M., Squarefree polynomials with prescribed coefficients . J. Number Theory 187(2018), 189–197. https://doi.org/10.1016/j.jnt.2017.10.025.Google Scholar
Pollack, P., Irreducible polynomials with several prescribed coefficients . Finite Fields Appl. 22(2013), 70–78. https://doi.org/10.1016/j.ffa.2013.03.001.Google Scholar
Tuxanidy, A. and Wang, Q., Irreducible polynomials with prescribed sums of coefficients. 2016. arxiv:1605.00351.Google Scholar