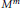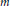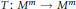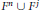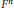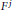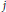Let ${{M}^{m}}$ be an $m$-dimensional, closed and smooth manifold, equipped with a smooth involution $T\,:\,{{M}^{m}}\,\to \,{{M}^{m}}$ whose fixed point set has the form ${{F}^{n}}\,\bigcup \,{{F}^{j}}$, where ${{F}^{n}}$ and ${{F}^{j}}$ are submanifolds with dimensions $n$ and $j$, 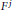${{F}^{j}}$ is indecomposable and 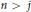$n\,>\,j$. Write 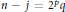$n\,-\,j\,={{2}^{p}}q$, where 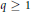$q\,\ge \,1$ is odd and 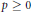$p\,\ge \,0$, and set 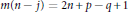$m(n\,-\,j)\,=\,2n\,+\,p\,-q\,+\,1$ if 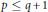$p\,\le \,q\,+\,1$ and 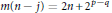$m(n\,-\,j)\,=\,2n\,+\,{{2}^{p-q}}$ if 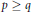$p\,\ge \,q$. In this paper we show that 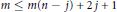$m\,\le \,m(n-j)+2j+1$. Further, we show that this bound is almost best possible, by exhibiting examples 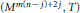$({{M}^{m(n-j)+2j}},\,T)$ where the fixed point set of $T$ has the form 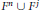${{F}^{n}}\,\bigcup \,{{F}^{j}}$ described above, for every 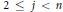$2\,\le \,j\,<\,n$ and 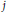$j$ not of the form 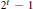${{2}^{t}}\,-\,1$ (for 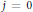$j\,=\,0$ and 2, it has been previously shown that 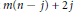$m(n\,-\,j)\,+\,2j$ is the best possible bound). The existence of these bounds is guaranteed by the famous 5/2-theorem of J. Boardman, which establishes that under the above hypotheses 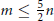$m\,\le \,\frac{5}{2}\,n$.