Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-25T02:15:01.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse Semigroups and Sheu's Groupoid for Odd Dimensional Quantum Spheres

Published online by Cambridge University Press:  20 November 2018

S. Sundar
S. Sundar*
Affiliation:
Indian Statistical Institute, Delhi, [email protected]
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we give a different proof of the fact that the odd dimensional quantum spheres are groupoid 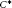${{C}^{*}}$-algebras. We show that the 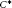${{C}^{*}}$-algebra 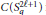$C\left( S_{q}^{2\ell +1} \right)$ is generated by an inverse semigroup $T$ of partial isometries. We show that the groupoid ${{\mathcal{G}}_{tight}}$ associated with the inverse semigroup $T$ by Exel is exactly the same as the groupoid considered by Sheu.

Keywords

46L9920M18inverse semigroupsgroupoidsodd dimensional quantum spheres
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 630 - 639
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Exel, R., Inverse semigroups and combinatorial C*-algebras. Bull. Braz. Math. Soc.(NS) 39 (2008), no. 2, 191–313. http://dx.doi.org/10.1007/s00574-008-0080-7 Google Scholar
[2] Hong, J. H. and Szymanski, W., Quantum spheres and projective spaces as graph algebras. Commun. Math. Phys. 232 (2002), no. 1, 157–188. http://dx.doi.org/10.1007/s00220-002-0732-1 Google Scholar
[3] Muhly, P. S. and Renault, J. N., C*-algebras of multivariable Wiener-Hopf operators. Trans. Amer. Math. Soc. 274 (1982), no. 1, 1–44.Google Scholar
[4] Pal, A. and Sundar, S., Regularity and dimension spectrum of the equivariant spectral triple for the odd-dimensional quantum spheres. J. Noncommut. Geom. 4 (2010), no. 3, 389–439.Google Scholar
[5] Sheu, A. J. L., Compact quantum groups and groupoid C*-algebras. J. Funct. Anal. 144 (1997), no. 2, 371–393. http://dx.doi.org/10.1006/jfan.1996.2999 Google Scholar
[6] Sheu, A. J. L., Quantum spheres as groupoid C*- algebras. Quart. J. Math. Oxford Ser. (2) 48 (1997), no. 192, 503–510. http://dx.doi.org/10.1093/qmath/48.4.503 Google Scholar
[7] Vaksman, L. L. and Soĭbel'man, Ya. S., Algebra of functions on the quantum group SU(n+ 1); and odd-dimensional quantum spheres. (Russian) Algebra i Analiz 2 (1990), no. 5, 101–120.Google Scholar
[8] Woronowicz, S. L., Compact matrix pseudogroups. Comm. Math. Phys. 111 (1987), no. 4, 613–665. http://dx.doi.org/10.1007/BF01219077 Google Scholar
[9] Woronowicz, S. L., Tannaka-Kreĭn duality for compact matrix pseudogroups. Twisted SU(N) groups. Invent. Math. 93 (1988), no. 1, 35–76. http://dx.doi.org/10.1007/BF01393687 Google Scholar
[10] Woronowicz, S. L., Compact quantum groups. In: Symétries quantiques (Les Houches, 1995), North-Holland, Amsterdam, 1998, pp. 845–884.Google Scholar