Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T16:01:17.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Inverse Laplace Transforms Encountered in Hyperbolic Problems of Non-Stationary Fluid-Structure Interaction

Published online by Cambridge University Press:  20 November 2018

Serguei Iakovlev
Serguei Iakovlev*
Affiliation:
Department of Engineering Mathematics and Internetworking, Dalhousie University, Halifax, NS, B3J 2X4 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper offers a study of the inverse Laplace transforms of the functions 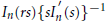${{I}_{n}}\left( rs \right)\,{{\{sI_{n}^{\prime }\,\left( s \right)\}}^{-1}}$ where 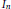${{I}_{n}}$ is the modified Bessel function of the first kind and $r$ is a parameter. The present study is a continuation of the author's previous work on the singular behavior of the special case of the functions in question, 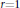$r=1$. The general case of 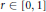$r\,\in \,\left[ 0,\,1 \right]$ is addressed, and it is shown that the inverse Laplace transforms for such $r$ exhibit significantly more complex behavior than their predecessors, even though they still only have two different types of points of discontinuity: singularities and finite discontinuities. The functions studied originate from non-stationary fluid-structure interaction, and as such are of interest to researchers working in the area.

Keywords

44A1044A2033C1040A3074F1076Q05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 50 , Issue 4 , 01 December 2007 , pp. 547 - 566
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions: with Formulas, Graphs and Mathematical Tables. Dover, New York, 1965.Google Scholar
[2] Erdelyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G., Higher Transcendental Functions. Vol. 1, McGraw-Hill, New York, 1953.Google Scholar
[3] Erdelyi, A., Magnus, W., Oberhettinger, F., and Tricomi, F. G., Higher Transcendental Functions. Vol. 2, McGraw-Hill, New York, 1953.Google Scholar
[4] Geers, T. L., Excitation of an elastic cylindrical shell by a transient acoustic wave. J. Appl. Mech. 36(1969), 459–469.Google Scholar
[5] Geers, T. L., Scattering of a transient acoustic wave by an elastic cylindrical shell. J. Acoustical Soc. Amer. 51(1972), 1640–1651.Google Scholar
[6] Iakovlev, S., Interaction of a spherical shock wave and a submerged fluid-filled circular cylindrical shell. J. Sound Vibration 225(2002), 615–633.Google Scholar
[7] Iakovlev, S., On the singular behavior of the inverse Laplace transforms of the functions . Canad. Math. Bull. 45(2002), no. 3, 399–416.Google Scholar
[8] Iakovlev, S., Influence of a rigid co-axial core on the stress-strain state of a submerged fluid-filled circular cylindrical shell subjected to a shock wave. J. Fluids Structures 19(2004), no. 7, 957–984.Google Scholar
[9] Iakovlev, S., Hydrodynamic shock loading on a submerged fluid-filled cylindrical shell. J. Fluids Struct. 22(2006), no. 8, 997–1028.Google Scholar
[10] Mair, H. U., Benchmarks for submerged structure response to underwater explosion. Shock and Vibration 6(1999), 169–181.Google Scholar