Hostname: page-component-586b7cd67f-vdxz6 Total loading time: 0 Render date: 2024-11-22T05:00:05.701Z Has data issue: false hasContentIssue false
  • English
  • Français

Insolvability of

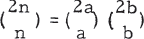
Published online by Cambridge University Press:  20 November 2018

L. Moser
L. Moser*
Affiliation:
University of Alberta, Research supported by American National Science Foundation
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A number of interesting Diophantine equations are of the a form f(n) = f(a) f(b). Thus the case f(a) = aa has been studied by C. Ko [2] and W. H. Mills [3] and a class of non-trivial solutions has been found, though whether these give all the solutions is still unsettled. The case f(n) = n! has been mentioned by W. Sierpinski. Here the situation is that besides the trivial solutions m! = m! 1! and (m!-1)! m! = (m!)! and the special solution 10! =7! 6! no other solutions are known, nor are they known not to exist. In the present note we show that the equation in the title has no solutions. A sketch of a somewhat different proof that this equation has at most a finite number of solutions was recently communicated to the author by P. Erdös.

Type
Notes on Number Theory V
Information
Canadian Mathematical Bulletin , Volume 6 , Issue 2 , May 1963 , pp. 167 - 169
Copyright
Copyright © Canadian Mathematical Society 1963

References

1. Erdös, P.. A theorem of Sylvester and Schur. Jour. JLond. Math. Soc. 9 (1934) pp. 282-288.Google Scholar
2. Jour, C. Ko.. Chinese Math. Soc. 2 (1940) pp. 205-207.Google Scholar
3. Mills, W. H.. An unsolved Diophantine equation. Proc. of the Instit. in theory of numbers, Boulder 1959.Google Scholar