Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T03:02:34.786Z Has data issue: false hasContentIssue false
  • English
  • Français

Injectivity of the Connecting Maps in AH Inductive Limit Systems

Published online by Cambridge University Press:  20 November 2018

George A. Elliott ,
Guihua Gong  and
Liangqing Li
George A. Elliott
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 3G3
Guihua Gong
Affiliation:
Department of Mathematics, University of Puerto Rico, San Juan, PR 00931, U.S.A.and Department of Mathematics, Hebei Normal University, Shijiazhuang, China
Liangqing Li
Affiliation:
Department of Mathematics, University of Puerto Rico, San Juan, PR 00931, U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 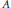$A$ be the inductive limit of a system

$${{A}_{1\,}}\,\xrightarrow{{{\phi }_{1,\,2}}}\,{{A}_{2}}\,\xrightarrow{{{\phi }_{2,\,3}}}\,{{A}_{3}}\,\to \cdots $$

with 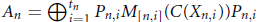${{A}_{n}}\,=\,\oplus _{i=1}^{{{t}_{n}}}\,{{P}_{n,\,i}}{{M}_{\left[ n,\,i \right]}}(C({{X}_{n,\,i}})){{P}_{n,\,i}}$, where 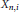${{X}_{n,\,i}}$ is a finite simplicial complex, and 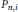${{P}_{n,\,i}}$ is a projection in 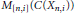${{M}_{[n,i]}}\,\left( C\left( {{X}_{n,i}} \right) \right)$. In this paper, we will prove that 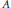$A$ can be written as another inductive limit

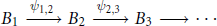$${{B}_{1}}\,\xrightarrow{{{\psi }_{1,\,2}}}\,{{B}_{2}}\,\xrightarrow{{{\psi }_{2,\,3}}}\,{{B}_{3}}\,\to \cdots $$

with 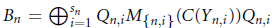${{B}_{n}}\,=\,\oplus _{i=1}^{{{s}_{n}}}\,{{Q}_{n,i}}{{M}_{\left\{ n,\,i \right\}}}(C({{Y}_{n,\,i}})){{Q}_{n,\,i}}$, where 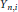${{Y}_{n,\,i}}$ is a finite simplicial complex, and 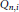${{Q}_{n,\,i}}$ is a projection in 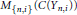${{M}_{\left\{ n,\,i \right\}}}(C({{Y}_{n,\,i}}))$, with the extra condition that all the maps 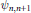${{\psi }_{n,n+1}}$ are injective. (The result is trivial if one allows the spaces 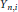${{Y}_{n,\,i}}$ to be arbitrary compact metrizable spaces.) This result is important for the classification of simple 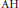$\text{AH}$ algebras. The special case that the spaces 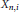${{X}_{n,\,i}}$ are graphs is due to the third author.

Keywords

46L0546L3519K14
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 1 , 01 March 2005 , pp. 50 - 68
Copyright
Copyright © Canadian Mathematical Society 2005

References

[Bl] Blackadar, B., Matricial and ultra-matricial topology. In: Operator Algebras,Mathematical Physics, and Low Dimensional Topology, (Herman, R. H. and Tanbay, B., eds.), A. K. Peters, Massachusetts, 1993, pp. 11–38.Google Scholar
[DL] Dădărlat, M. and Loring, T., A universal multi-coefficient theorem for the Kasparov groups., Duke Math. J. 84(1996), 355–377.Google Scholar
[DNNP] Dadarlat, M., Nagy, G., Nemethi, A. and Pasnicu, C., Reduction of topological stable rank in inductive limits of C*-algebras. Pacific J. Math. 153(1992), 267–276.Google Scholar
[Ell1] Elliott, G. A., A classification of certain simple C*-algebras. In: Quantum and Non-Commutative Analysis, ( Araki, H. et al. eds.) Kluwer, Dordrecht, 1993, pp. 373–385.Google Scholar
[Ell2] Elliott, G. A., A classification of certain simple C*-algebras, II. J. Ramanujan Math. Soc. 12(1997), 97–134.Google Scholar
[Ell3] Elliott, G. A., On the classification of C*-algebras of real rank zero. J. Reine Angew. Math. 443(1993), 179–219.Google Scholar
[EG] Elliott, G. A. and Gong, G., On the classification of C*-algebras of real rank zero, II. Ann. of Math. 144(1996), 497–610.Google Scholar
[EGL] Elliott, G. A., Gong, G., and Li, L., On the classification of simple inductive limit C*-algebras, II: The isomorphism theorem, preprint.Google Scholar
[G1] Gong, G., On the classification of simple inductive limit C*-algebras, I. Documenta Math. 7(2002), 255–461.Google Scholar
[G2] Gong, G., Simple inductive limit C*-algebras with very slow dimension growth: An appendix to “On the classification of simple inductive limit C*-algebras, I”, preprint.Google Scholar
[Li1] Li, L., Classification of simple C*-algebras—inductive limits of matrix algebras over trees, Memoirs Amer. Math. Soc., 605, 1996.Google Scholar
[Li2] Li, L., Simple inductive limit C*-algebras: Spectra and approximation by interval algebras. J. Reine Angew. Math. 507(1999), 57–79.Google Scholar
[Li3] Li, L., Classification of simple C*-algebras: inductive limit of matrix algebras over 1-dimensional spaces. J. Funct. Anal. 192(2002), 1–51.Google Scholar
[NT] Nielsen, K. E. and Thomsen, K., Limits of circle algebras. Expos. Math. 14(1996), 17–56.Google Scholar
[P] Pasnicu, C., Shape equivalence, nonstable K-theory and AH algebras Pacific J. Math. 192(2000), 159–182.Google Scholar
[R] Rordam, M., Classification of certain infinite simple C*-algebras. J. Funct. Anal. 131(1995), 415–458.Google Scholar
[T] Thomsen, K., Inductive limits of interval algebras. Amer. J. Math. 116(1994), 605–620.Google Scholar