Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T17:49:42.974Z Has data issue: false hasContentIssue false
  • English
  • Français

Injectivity of the Connecting Homomorphisms in Inductive Limits of Elliott–Thomsen Algebras

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  07 January 2019

Zhichao Liu
Zhichao Liu*
Affiliation:
Postdoctoral Research Station of Mathematics, Hebei Normal University, Shijiazhuang, 050024, China Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 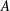$A$ be the inductive limit of a sequence

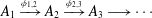$$\begin{eqnarray}A_{1}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{1,2}}A_{2}\xrightarrow[{}]{\unicode[STIX]{x1D719}_{2,3}}A_{3}\longrightarrow \cdots\end{eqnarray}$$
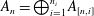with $A_{n}=\bigoplus _{i=1}^{n_{i}}A_{[n,i]}$, where all the 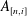$A_{[n,i]}$ are Elliott–Thomsen algebras and 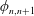$\unicode[STIX]{x1D719}_{n,n+1}$ are homomorphisms. In this paper, we will prove that 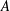$A$ can be written as another inductive limit
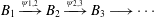$$\begin{eqnarray}B_{1}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{1,2}}B_{2}\xrightarrow[{}]{\unicode[STIX]{x1D713}_{2,3}}B_{3}\longrightarrow \cdots\end{eqnarray}$$
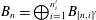 with $B_{n}=\bigoplus _{i=1}^{n_{i}^{\prime }}B_{[n,i]^{\prime }}$, where all the 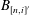$B_{[n,i]^{\prime }}$ are Elliott–Thomsen algebras and with the extra condition that all the 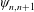$\unicode[STIX]{x1D713}_{n,n+1}$ are injective.

Keywords

injectiveinductive limitElliott–Thomsen algebra

MSC classification

Primary: 46L05: General theory of $C^*$-algebras
Secondary: 46L35: Classifications of $C^*$-algebras
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 131 - 148
Copyright
© Canadian Mathematical Society 2018 

References

Blackadar, B., Bratteli, O., Elliott, G. A., and Kumjian, A., Reduction of real rank in inductive limits of C ∗-algebras . Math. Ann. 292(1992), 111–126. https://doi.org/10.1007/BF01444612.Google Scholar
Elliott, G. A., A classification of certain simple C ∗-lgebras . In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer Acad. Publ., Dordrecht, 1993, pp. 373–385.Google Scholar
Elliott, G. A., On the classification of C ∗-algebras of real rank zero . J. Reine. Angew. Math. 443(1993), 179–219. https://doi.org/10.1515/crll.1993.443.179.Google Scholar
Elliott, G. A., A classification of certain simple C ∗-algebras, II . J. Ramanujan Math. Soc. 12(1997), 97–134.Google Scholar
Elliott, G. A., Gong, G., and Li, L., Injectivity of the connecting maps in AH inductive systems . Canad. Math. Bull. 48(2005), 50–68. https://doi.org/10.4153/CMB-2005-005-9.Google Scholar
Eliott, G. A. and Thomsen, K., The state space of the K 0-group of a simple separable C ∗-algebra . Geom. Funct. Anal. 4(1994), 522–538. https://doi.org/10.1007/BF01896406.Google Scholar
Gong, G., On the classification of simple inductive limit C ∗-algebras, I. The reduction theorem . Doc. Math. 7(2002), 255–461.Google Scholar
Gong, G. and Lin, H., On classification of simple non-unital amenable C ∗-algebras, II. arxiv:1702.01073.Google Scholar
Gong, G., Lin, H., and Niu, Z., Classification of finite simple amenable ${\mathcal{Z}}$ -stable C ∗-algebras. arxiv:1501.00135v6.Google Scholar
Li, L., Classification of simple C ∗-algebras inductive limits of matrix algebras over trees . Mem. Amer. Math. Soc. 127(1997), no. 605.Google Scholar
Li, L., Simple inductive limit C ∗-algebras: Spectra and approximation by interval algebras . J. Reine Angew. Math. 507(1999), 57–79. https://doi.org/10.1515/crll.1999.019.Google Scholar
Li, L., Classification of simple C ∗-algebras: inductive limit of matrix algebras over 1-dimensional spaces . J. Funct. Anal. 192(2002), 1–51. https://doi.org/10.1006/jfan.2002.3895.Google Scholar
Liu, Z., A decomposition theorem for real rank zero inductive limits of 1-dimensional non-commutative CW complexes. arxiv:1709.03684v1.Google Scholar
Su, H., On the classification of C ∗-algebras of real rank zero: Inductive limits of matrix algebras over non-Hausdorff graphs . Mem. Amer. Math. Soc. 114(1995), no. 547. https://doi.org/10.1090/memo/0547.Google Scholar