Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T20:08:22.334Z Has data issue: false hasContentIssue false
  • English
  • Français

The Initial and Terminal Cluster Sets of an Analytic Curve

Published online by Cambridge University Press:  20 November 2018

Paul M. Gauthier
Paul M. Gauthier*
Affiliation:
Département de mathématiques et de statistique, Université de Montréal, Pavillon André-Aisenstadt, 2920, chemin de la Tour, Montréal H3T 1J4, Québec email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For an analytic curve 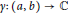$\gamma :\,\left( a,\,b \right)\,\to \,\mathbb{C}$, the set of values approached by 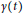$\gamma \left( t \right)$, as 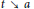$t\,\searrow \,\,a$ and as 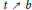$t\,\nearrow \,b$ can be any two continua of 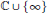$\mathbb{C}\,\cup \,\left\{ \infty \right\}$.

Keywords

30B40analytic curvecluster set
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 2 , 01 June 2018 , pp. 282 - 288
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Collingwood, E. F. and Lohwater, A. J., The theory of düster sets. Cambridge Tracts in Mathematics and Mathematical Physics, 56, Cambridge University Press, Cambridge 1966.Google Scholar
[2] Gauthier, P. M. and Kienzle, J., Approximation ofafunction and its derivatives by entire functions. Canad. Math. Bull. 59(2016), no. 1, 87–94. http://dx.doi.Org/10.4153/CMB-2015-060-5 Google Scholar
[3] Gauthier, P. M. and Nestoridis, V., Conformal extensions of functions defined on arbitrary subsets of Riemann surfaces. Arch. Math. (Basel) 104(2015), no. 1, 61–67.http://dx.doi.Org/10.1007/s000I3-014-0716-3 Google Scholar
[4] Hoischen, L., Approximation und Interpolation durch ganze Funktionen. (German) J. Approximation Theory 15(1975), no. 2, 116–123.http://dx.doi.org/10.1016/0021-9045(75)90121-5 Google Scholar
[5] Nestoridis, V. and Papadopoulos, A., Are length as a global conformal parameter for analytic curves. J.Math. Anal. Appl. 445(2017), no. 2, 1505–1515.http://dx.doi.Org/10.1016/j.jmaa.2016.02.031 Google Scholar