Hostname: page-component-5cf477f64f-mgq6s Total loading time: 0 Render date: 2025-04-04T13:43:52.790Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite Powers and Cohen Reals

Published online by Cambridge University Press:  20 November 2018

Andrea Medini ,
Jan van Mill  and
Lyubomyr Zdomskyy
Andrea Medini
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, University of Vienna, Währinger Strasse 25, A-1090 Wien, Austria, e-mail : [email protected] , [email protected]
Jan van Mill
Affiliation:
Korteweg-de Vries Institute for Mathematics, University of Amsterdam, Science Park 105-107, P. O. Box 94248, 1090 GE Amsterdam, Netherlands, e-mail : [email protected]
Lyubomyr Zdomskyy
Affiliation:
Kurt Gödel Research Center for Mathematical Logic, University of Vienna, Währinger Strasse 25, A-1090 Wien, Austria, e-mail : [email protected] , [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a consistent example of a zero-dimensional separable metrizable space $Z$ such that every homeomorphism of ${{Z}^{\omega }}$ acts like a permutation of the coordinates almost everywhere. Furthermore, this permutation varies continuously. This shows that a result of Dow and Pearl is sharp, and gives some insight into an open problem of Terada. Our example $Z$ is simply the set of ${{\omega }_{1}}$ Cohen reals, viewed as a subspace of 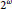${{2}^{\omega }}$.

Keywords

03E3554B1054G20infinite powerzero-dimensionalfirst-countablehomogeneousCohen realrigidh-homogeneous
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 4 , 01 December 2018 , pp. 812 - 821
Copyright
Copyright © Canadian Mathematical Society 2018

References

[AvM] ArkhangeFskii, A. V. and van Mill, J., Topological homogeneity. In: Recent progress in general topology. III. Atlantis Press, Paris, 2014, pp. 1–68. http://dx.doi.Org/10.2991/978-94-6239-024-9_1Google Scholar
[DP] Dow, A. and Pearl, E., Homogeneity in powers of zero-dimensional first-countable spaces. Proc. Amer. Math. Soc. 125 (1997), no. 8, 2503-2510. http://dx.doi.org/10.1090/S0002-9939-97-03998-1Google Scholar
[vE] van Engelen, E., On the homogeneity of infinite products. Topology Proc. 17 (1992), 303–315.Google Scholar
[En] Engelking, R., General topology. Second éd., Sigma Series in Pure Mathematics, 6, Heldermann Verlag, Berlin, 1989.Google Scholar
[FZ] Fitzpatrick, B. Jr. and Zhou, H. X., Some open problems in densely homogeneous spaces. In: Open problems in topology, North-Holland, Amsterdam, 1990, pp. 251–259.Google Scholar
[Gr] Gruenhage, G., New classic problems: Homogeneity ofX°°. Topology Proc. 15 (1990), 207–208.Google Scholar
[Je] Jech, T., Set theory. The third millennium éd., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[Kec] Kechris, A. S., Classical descriptive set theory. Graduate Texts in Mathematics, 156, Springer-Verlag, New York, 1995. http://dx.doi.org/!0.1007/978-1-4612-4190-4Google Scholar
[Kel] Keller, O.-H., Die Homoiomorphie der kompakten konvexen Mengen in Hilbertschen Raum. Math. Ann. 105 (1931), 748–758. http://dx.doi.org/10.1007/BF01455844Google Scholar
[Ku] Kunen, K., Set theory. Studies in Logic (London), 34, College Publications, London, 2011.Google Scholar
[La] Lawrence, L. B., A rigid subspace of the real line whose square is a homogeneous subspace of the plane. Trans. Amer. Math. Soc. 357 (2005), no. 7, 2535-2556. http://dx.doi.org/10.1090/S0002-9947-05-03212-5Google Scholar
[Mel] Medini, A., Products and h-homogeneity. Topology Appl. 158 (2011), no. 18, 2520-2527. http://dx.doi.Org/10.1016/j.topol.2011.08.011Google Scholar
[Me2] Medini, A., The topology of ultrafilters as subspaces of the Cantor set and other topics. Ph.D. Thesis, University of Wisconsin - Madison, ProQuest LLC, Ann Arbor, MI, 2013.Google Scholar
[Me3] Medini, A., Countable dense homogeneity in powers of zero-dimensional definable spaces. Canad. Math. Bull. 58 (2015), no. 2, 334-349. http://dx.doi.Org/10.4153/CMB-2014-062-6Google Scholar
[MvMZ] Medini, A., van Mill, J., and Zdomskyy, L., A homogeneous space whose complement is rigid. Israel J. Math. 214 (2016), no. 2, 583-595. http://dx.doi.Org/10.1007/s11856-016-1348-zGoogle Scholar
[Mv] Medvedev, S. V., On properties of h-homogeneous spaces with the Baire property. Topology Appl. 159 (2012), no. 3, 679-694. http://dx.doi.Org/10.1016/j.topol.2011.10.016Google Scholar
[Ox] Oxtoby, J. C., Cartesian products of Baire spaces. Fund. Math. 49(1960/1961), 157–166. http://dx.doi.org/10.4064/fm-49-2-157-166Google Scholar
[Ro] Roy, P., Nonequality of dimensions for metric spaces. Trans. Amer. Math. Soc. 134 (1968), 117–132. http://dx.doi.org/10.1090/S0002-9947-1968-0227960-2Google Scholar
[Te] Terada, T., Spaces whose all nonempty clopen subsets are homeomorphic. Yokohama Math. J. 40 (1993), no. 2, 87-93.Google Scholar