Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T05:57:43.554Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite Classes of Covering Numbers

Published online by Cambridge University Press:  20 November 2018

I. Bluskov ,
M. Greig  and
K. Heinrich
I. Bluskov
Affiliation:
Department of Mathematics and Computer Science, University of Northern British Columbia, Prince George, BC, V2N 5M2, email: [email protected]
M. Greig
Affiliation:
Greig Consulting, 207-170 East Fifth Street, North Vancouver, BC, V7L 4L4, email: [email protected]
K. Heinrich
Affiliation:
University of Regina, Regina, Saskatchewan, S4S 0A2, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 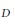$D$ be a family of $k$-subsets (called blocks) of a 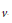$v$-set 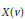$X\left( v \right)$. Then 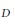$D$ is a 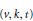$\left( v,\,k,\,t \right)$ covering design or covering if every 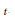$t$-subset of 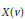$X\left( v \right)$ is contained in at least one block of 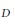$D$. The number of blocks is the size of the covering, and the minimum size of the covering is called the covering number. In this paper we consider the case 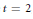$t\,=\,2$, and find several infinite classes of covering numbers. We also give upper bounds on other classes of covering numbers.

Keywords

05B4005D05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 4 , 01 December 2000 , pp. 385 - 396
Copyright
Copyright © Canadian Mathematical Society 2000

References

[1] Baker, R. D., An elliptic semiplane. J. Combin. Theory Ser. A 25 (1978), 193–195.Google Scholar
[2] Bluskov, I., Some t-Designs are Minimal (t + 1)-Coverings. Discrete Math. 188 (1998), 245–251.Google Scholar
[3] Gordon, D. M., Kuperberg, G. and Patashnik, O., New Constructions for Covering Designs. J. Combin. Des. 3 (1995), 269–284.Google Scholar
[4] Mathon, R., On a new divisible semiplane. Unpublished manuscript.Google Scholar
[5] Mills, W. H. and Mullin, R. C., Coverings and Packings. In: Contemporary Design Theory: A Collection of Surveys (eds. J. H. Dinitz and D. R. Stinson), Wiley, 1992, 371–399.Google Scholar
[6] Schönheim, J., On Coverings. Pacific J. Math. 14 (1964), 1405–1411.Google Scholar
[7] Shrikhande, S. S., A note on mutually orthogonal Latin squares. Shankhyā A 23 (1961), 115–116.Google Scholar
[8] Todorov, D. T., Some coverings derived from finite planes. In: Finite and Infinite Sets, Vol. 2 (eds. A. Hajnal, L. Lovász and V. T. Śos), Colloq. Math. Soc. Janos Bolyai 37, Elsevier, New York, 1984, 697–710.Google Scholar