Article contents
Inadmissibility of the Maximum Likelihood Estimator in the Presence of Prior Information
Published online by Cambridge University Press: 20 November 2018
Extract
Lehmann [1] in his lecture notes on estimation shows that for estimating the unknown mean of a normal distribution, N(θ, 1), the usual estimator 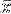 is neither minimax nor admissible if it is known that θ belongs to a finite closed interval [a, b] and the loss function is squared error. It is shown that
is neither minimax nor admissible if it is known that θ belongs to a finite closed interval [a, b] and the loss function is squared error. It is shown that 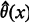 , the maximum likelihood estimator (MLE) of θ, has uniformly smaller mean squared error (MSE) than that of
, the maximum likelihood estimator (MLE) of θ, has uniformly smaller mean squared error (MSE) than that of 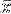 . It is natural to ask the question whether the MLE
. It is natural to ask the question whether the MLE 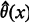 of θ in N(θ, 1) is admissible or not if it is known that θ ∊ [a, b]. The answer turns out to be negative and the purpose of this note is to present this result in a slightly generalized form.
of θ in N(θ, 1) is admissible or not if it is known that θ ∊ [a, b]. The answer turns out to be negative and the purpose of this note is to present this result in a slightly generalized form.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1970
References
- 4
- Cited by


