Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Grätzer, George
and
Kelly, David
1988.
Subdirectly irreducible members of products of lattice varieties.
Proceedings of the American Mathematical Society,
Vol. 102,
Issue. 3,
p.
483.
Freese, Ralph
Pickering, Douglas
and
Roddy, Michael
1991.
Obituary: A. Alan Day.
Order,
Vol. 8,
Issue. 4,
p.
319.
Czédli, Gábor
2009.
Sums of Lattices and a Relational Category.
Order,
Vol. 26,
Issue. 4,
p.
309.


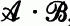 of two subclasses of a given variety of algebras,
of two subclasses of a given variety of algebras, 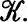 Following the group theorectic example, members of
Following the group theorectic example, members of 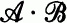 were called extensions of algebras in
were called extensions of algebras in  by algebras in
by algebras in