Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-25T06:02:52.774Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperplanes of the Form f1(x, y)z1 + · · · + fk(x, y)zk + g(x, y) Are Variables

Published online by Cambridge University Press:  20 November 2018

Stéphane Vénéreau
Stéphane Vénéreau*
Affiliation:
Mathematisches Institut, Universität Basel, Rheinsprung 21, 4051 Basel, switzerland e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Abhyankar–Sathaye Embedded Hyperplane Problem asks whether any hypersurface of 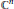${{\mathbb{C}}^{n}}$ isomorphic to 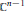${{\mathbb{C}}^{n-1}}$ is rectifiable, i.e., equivalent to a linear hyperplane up to an automorphism of 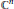${{\mathbb{C}}^{n}}$. Generalizing the approach adopted by Kaliman, Vénéreau, and Zaidenberg, which consists in using almost nothing but the acyclicity of 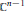${{\mathbb{C}}^{n-1}}$, we solve this problem for hypersurfaces given by polynomials of 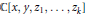$\mathbb{C}\left[ x,y,{{z}_{1}},...,{{z}_{k}} \right]$ as in the title.

Keywords

14R1014R25variablesAbhyankar–Sathaye Embedding Problem
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 4 , 01 December 2005 , pp. 622 - 635
Copyright
Copyright © Canadian Mathematical Society 2005

References

[AM75] Abhyankar, S. S. and Moh, T. T., Embeddings of the line in the plane. J. Reine Angew.Math. 276(1975), 148–166.Google Scholar
[BCW77] Bass, H., Connell, E. H., and Wright, D. L., Locally polynomial algebras are symmetric algebras. Invent.Math. 38(1976/77), 279–299.Google Scholar
[Dol72] Dold, A., Lectures on Algebraic Topology. Die Grundlehren der mathematischen Wissenschaften 200, Springer-Verlag, New York, 1972.Google Scholar
[Dur87] Durfee, A. H., Algebraic varieties which are a disjoint union of subvarieties. In: Geometry and Topology, Lecture Notes in Pure and Appl. Math. 105, Dekker, New York, 1987, pp. 99–102.Google Scholar
[EV99] Edo, E. and Vénéreau, S., Length 2 variables of A[x, y] and transfer. Ann. Polin. Math. 76(2001), 67–76.Google Scholar
[Fuj82] Fujita, T., On the topology of noncomplete algebraic surfaces. J. Fac. Sci. Univ. Tokyo Sect. IA Math. 29(1982), 503–566.Google Scholar
[Kal94] Kaliman, Sh., Exotic analytic structures and Eisenman intrinsic measures. Israel J. Math. 88(1994), 411–423.Google Scholar
[KVZ01] Kaliman, Sh., Vénéreau, S., and Zaidenberg, M., Extensions birationnelles simples de l’anneau de polynmes ℂ3 . C. R. Acad. Sci. Paris Sér. I Math. 333(2001), 319–322.Google Scholar
[KVZ04] Kaliman, Sh., Vénéreau, S., and Zaidenberg, M., Simple birational extensions of the polynomial ring ℂ[3] . Trans. Amer.Math. Soc. 356(2004), 509–555.Google Scholar
[KZ99] Kaliman, Sh. and Zaidenberg, M., Affine modifications and affine hypersurfaces with a very transitive automorphism group. Transform. Groups 4(1999), 53–95.Google Scholar
[Mas80] Massey, W. S., Singular Homology Theory. Graduate Texts in Mathematics 70, Springer-Verlag, New York, 1980.Google Scholar
[Rus76] Russell, P., Simple birational extensions of two dimensional affine rational domains. Compositio Math. 33(1976), 197–208.Google Scholar
[Sat76] Sathaye, A., On linear planes. Proc. Amer.Math. Soc. 56(1976), 1–7.Google Scholar
[Ses58] Seshadri, C. S., Triviality of vector bundles over the affine space k 2 . Proc. Natl. Acad. Sci. U.S.A. 44(1958), 456–458.Google Scholar
[Suz74] Suzuki, M., Propriétés topologiques des polynômes de deux variables complexes, et automorphismes algébriques de l’espaceℂ2 . J. Math. Soc. Japan 26(1974), 241–257.Google Scholar
[Vn01] Vénéreau, S., Automorphismes et variables de l’anneau de polynômes A[y 1, … , yn ]. Ph.D. thesis, Université Grenoble I, Institut Fourier, 2001.Google Scholar
[Zaĭ85] Zaĭdenberg, M. G., Rational actions of the group ℂ* on ℂ2 , their quasi-invariants and algebraic curves in ℂ2 with Euler characteristic 1 . Dokl. Akad. Nauk SSSR 280(1985), 277–280, (Russian), Soviet Math. Dokl. 31(1985), 57–60.Google Scholar
[ZL83] Zaĭdenberg, M. G. and Lin, V. Ya., An irreducible, simply connected algebraic curve in ℂ2 is equivalent to a quasihomogeneous curve. Dokl. Akad. Nauk SSSR 271(1983), 1048–1052, (Russian), Soviet Math. Dokl. 28(1983), 200–204.Google Scholar