Hostname: page-component-5cf477f64f-rdph2 Total loading time: 0 Render date: 2025-04-08T05:05:13.575Z Has data issue: false hasContentIssue false
  • English
  • Français

A Hypergraph with Commuting Partial Laplacians

Published online by Cambridge University Press:  20 November 2018

Cristina M. Ballantine
Cristina M. Ballantine*
Affiliation:
Department of Mathematics University of Toronto Toronto, Ontario M5A 3G3 Department of Mathematics Bowdoin College Brunswick, Maine 04011 U.S.A., email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 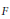$F$ be a totally real number field and let 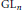$\text{G}{{\text{L}}_{n}}$ be the general linear group of rank 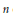$n$ over 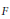$F$. Let 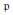$\mathfrak{p}$ be a prime ideal of 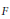$F$ and 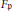${{F}_{\mathfrak{p}}}$ the completion of 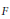$F$ with respect to the valuation induced by 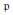$\mathfrak{p}$. We will consider a finite quotient of the affine building of the group 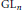$\text{G}{{\text{L}}_{n}}$ over the field 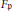${{F}_{\mathfrak{p}}}$. We will view this object as a hypergraph and find a set of commuting operators whose sum will be the usual adjacency operator of the graph underlying the hypergraph.

Keywords

11F2520F32Hecke operatorsbuildings
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 4 , 01 December 2001 , pp. 385 - 397
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Ballantine, C., Hypergraphs and Automorphic Forms. PhD Thesis, Toronto, 1998.Google Scholar
[2] Bollobas, B.. Extremal Graph Theory. LMS Monographs, Academic Press 1978.Google Scholar
[3] Borel, A.. Linear algebraic groups. Springer-Verlag 1991.Google Scholar
[4] Borel, A., Some finiteness properties of adele groups over number fields. Inst.Hautes Études Sci. Publ. Math. 16 (1963), 5–30.Google Scholar
[5] Brown, K. S.. Buildings. Springer-Verlag, New York, 1989.Google Scholar
[6] Cartier, P.. Representations of p-adic groups: A survey. Automorphic forms, representations, and L-functions, Proc. Sympos. Pure Math. 33, Part I (eds. A. Borel and W. Casselman), Amer.Math. Soc., Providence, R.I. 1979, 111–155.Google Scholar
[7] Lubotzky, A.. Discrete groups, expanding graphs and invariant measures. Progress in Math. 125, Birkhauser Verlag, 1994.Google Scholar
[8] Rogawski, J. D.. Automorphic representations of the unitary group in three variables. Ann. of Math. Studies 123, Princeton Univ. Press, Princeton, New Jersey, 1990.Google Scholar
[9] Selberg, A.. On discontinuous groups in higher-dimensional symmetric spaces. Contributions to Function Theory, International Colloquia on Function Theory, Bombay, 1960, 147–164, Tata Institute of Fundamental Research, Bombay, 1960.Google Scholar
[10] Tits, J.. Reductive groups over local fields. Automorphic forms, representations, and L-functions, Proc. Sympos. Pure Math. 33, Part I (eds. A. Borel and W. Casselman), Amer. Math. Soc., Providence, R.I. 1979, 29–69.Google Scholar