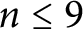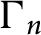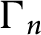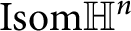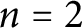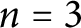1 Introduction
Let
![]() $\mathbb H^{n}$
denote the real hyperbolic n-space with its isometry group
$\mathbb H^{n}$
denote the real hyperbolic n-space with its isometry group
![]() $\textrm{Isom}\mathbb H^{n}$
.
$\textrm{Isom}\mathbb H^{n}$
.
A hyperbolic Coxeter polyhedron
![]() $P\subset \mathbb H^{n}$
is a convex polyhedron of finite volume all of whose dihedral angles are integral submultiples of
$P\subset \mathbb H^{n}$
is a convex polyhedron of finite volume all of whose dihedral angles are integral submultiples of
![]() $\pi $
. Associated to P is the hyperbolic Coxeter group
$\pi $
. Associated to P is the hyperbolic Coxeter group
![]() $\Gamma \subset \textrm{Isom}\mathbb H^{n}$
generated by the reflections in the bounding hyperplanes of P. By construction,
$\Gamma \subset \textrm{Isom}\mathbb H^{n}$
generated by the reflections in the bounding hyperplanes of P. By construction,
![]() $\Gamma $
is a discrete group with associated orbifold
$\Gamma $
is a discrete group with associated orbifold
![]() $O^{n}=\mathbb H^{n} / \Gamma $
of finite volume.
$O^{n}=\mathbb H^{n} / \Gamma $
of finite volume.
We focus on non-compact hyperbolic Coxeter polyhedra, having at least one ideal vertex
![]() $v_{\infty } \in \partial \mathbb H^{n}$
. Notice that the stabilizer of the vertex
$v_{\infty } \in \partial \mathbb H^{n}$
. Notice that the stabilizer of the vertex
![]() $v_{\infty }$
is isomorphic to an affine Coxeter group. The group
$v_{\infty }$
is isomorphic to an affine Coxeter group. The group
![]() $\Gamma $
is called non-cocompact, and its quotient space
$\Gamma $
is called non-cocompact, and its quotient space
![]() $O^{n}$
has at least one cusp.
$O^{n}$
has at least one cusp.
The hyperbolic Coxeter group
![]() $\Gamma $
is the geometric realization of an abstract Coxeter system
$\Gamma $
is the geometric realization of an abstract Coxeter system
![]() $(W,S)$
consisting of a group W with a finite generating set S together with the relations
$(W,S)$
consisting of a group W with a finite generating set S together with the relations
![]() $s^{2}=1$
and
$s^{2}=1$
and
![]() $(ss^{\prime })^{m_{ss^{\prime }}}=1$
, where
$(ss^{\prime })^{m_{ss^{\prime }}}=1$
, where
![]() $m_{ss^{\prime }}=m_{s^{\prime }s}\in \{2,3,\ldots ,\infty \}$
for all
$m_{ss^{\prime }}=m_{s^{\prime }s}\in \{2,3,\ldots ,\infty \}$
for all
![]() $s,s^{\prime }\in S$
with
$s,s^{\prime }\in S$
with
![]() $s\not =s^{\prime }$
. The growth series
$s\not =s^{\prime }$
. The growth series
![]() $f_{S}(t)$
of
$f_{S}(t)$
of
![]() $W=(W,S)$
is given by
$W=(W,S)$
is given by
 $$ \begin{align*}f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k} \, , \end{align*} $$
$$ \begin{align*}f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k} \, , \end{align*} $$
where
![]() $a_{k}\in \mathbb Z$
is the number of elements in W with S-length k. The growth rate
$a_{k}\in \mathbb Z$
is the number of elements in W with S-length k. The growth rate
![]() $\tau _{W}$
of
$\tau _{W}$
of
![]() $W=(W,S)$
is defined as the inverse of the radius of convergence of
$W=(W,S)$
is defined as the inverse of the radius of convergence of
![]() $f_{S}(t)$
.
$f_{S}(t)$
.
We are interested in small growth rates of non-cocompact hyperbolic Coxeter groups in
![]() $\textrm{Isom}\mathbb H^{n}$
for
$\textrm{Isom}\mathbb H^{n}$
for
![]() $n\geq 2$
. For
$n\geq 2$
. For
![]() $n=2$
, Floyd [Reference Floyd6] showed that the Coxeter group
$n=2$
, Floyd [Reference Floyd6] showed that the Coxeter group
![]() $\Gamma _{2} = [3,\infty ]$
generated by the reflections in the triangle with angles
$\Gamma _{2} = [3,\infty ]$
generated by the reflections in the triangle with angles
![]() $\pi /2, \pi /3$
, and
$\pi /2, \pi /3$
, and
![]() $0$
is the (unique) group of minimal growth rate. For
$0$
is the (unique) group of minimal growth rate. For
![]() $n=3$
, Kellerhals [Reference Kellerhals13] proved that the tetrahedral group
$n=3$
, Kellerhals [Reference Kellerhals13] proved that the tetrahedral group
![]() $\Gamma _{3}$
generated by the reflections in the Coxeter tetrahedron with symbol
$\Gamma _{3}$
generated by the reflections in the Coxeter tetrahedron with symbol
![]() $[6,3,3]$
realizes minimal growth rate in a unique way.
$[6,3,3]$
realizes minimal growth rate in a unique way.
Consider the hyperbolic Coxeter n-simplices and their reflection groups
![]() $\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$
depicted in Table 1. For their volumes, we refer to [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]. Observe that
$\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$
depicted in Table 1. For their volumes, we refer to [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]. Observe that
![]() $\Gamma _{n}$
is of minimal covolume among all non-cocompact hyperbolic Coxeter n-simplex groups.
$\Gamma _{n}$
is of minimal covolume among all non-cocompact hyperbolic Coxeter n-simplex groups.
Table 1 The hyperbolic Coxeter n-simplex group
![]() $\Gamma _{n}$
.
$\Gamma _{n}$
.

The aim of this work is to prove the following result in the context of growth rates.
Theorem Let
![]() $2\leq n \leq 9$
. Among all non-cocompact hyperbolic Coxeter groups of finite covolume in
$2\leq n \leq 9$
. Among all non-cocompact hyperbolic Coxeter groups of finite covolume in
![]() $\operatorname {Isom} \mathbb H^{n}$
, the group
$\operatorname {Isom} \mathbb H^{n}$
, the group
![]() $\Gamma _{n}$
given in Table 1 has minimal growth rate, and as such the group is unique.
$\Gamma _{n}$
given in Table 1 has minimal growth rate, and as such the group is unique.
Our Theorem should be compared with the volume minimality results for cusped hyperbolic n-orbifolds
![]() $O^{n}$
for
$O^{n}$
for
![]() $2\le n \le 9$
. These results are due to Siegel [Reference Siegel16] for
$2\le n \le 9$
. These results are due to Siegel [Reference Siegel16] for
![]() $n=2$
, Meyerhoff [Reference Meyerhoff15] for
$n=2$
, Meyerhoff [Reference Meyerhoff15] for
![]() $n= 3$
, Hild and Kellerhals [Reference Hild and Kellerhals10] for
$n= 3$
, Hild and Kellerhals [Reference Hild and Kellerhals10] for
![]() $n=4$
, and Hild [Reference Hild9] for
$n=4$
, and Hild [Reference Hild9] for
![]() $n\le 9$
. Indeed, the fundamental group of
$n\le 9$
. Indeed, the fundamental group of
![]() $O^{n}$
is related to
$O^{n}$
is related to
![]() $\Gamma _{n}$
in all these cases.
$\Gamma _{n}$
in all these cases.
The work is organized as follows. In Section 2.1, we set the background about hyperbolic Coxeter polyhedra and their associated reflection groups. Furthermore, we present a result of Felikson and Tumarkin about their combinatorics as given by [Reference Felikson and Tumarkin5, Theorem B], which will play a crucial role in our proof. In fact, we will exploit the (non-)simplicity of the Coxeter polyhedra in a most useful way. In Section 2.2, we discuss growth series and growth rates of Coxeter groups and introduce the notion of extension of a Coxeter graph. We also provide some illustrating examples. The monotonicity result of Terragni [Reference Terragni18] for growth rates, presented in Theorem 2.2, will be another major ingredient in our proof. Finally, Section 3 is devoted to the proof of our result. We perform it in two steps by assuming that the Coxeter graph under consideration has an affine component of type
![]() $\widetilde A_{1}$
or not.
$\widetilde A_{1}$
or not.
2 Hyperbolic Coxeter groups and growth rates
2.1 Coxeter polyhedra and their reflection groups
Let
![]() $\mathbb X^{n}$
denote one of the geometric n-spaces of constant curvature, the unit n-sphere
$\mathbb X^{n}$
denote one of the geometric n-spaces of constant curvature, the unit n-sphere
![]() $\mathbb S^{n}$
, the Euclidean n-space
$\mathbb S^{n}$
, the Euclidean n-space
![]() $\mathbb E^{n}$
, or the real hyperbolic n-space
$\mathbb E^{n}$
, or the real hyperbolic n-space
![]() $\mathbb H^{n}$
. As usual, we embed
$\mathbb H^{n}$
. As usual, we embed
![]() $\mathbb X^{n}$
in a suitable quadratic space
$\mathbb X^{n}$
in a suitable quadratic space
![]() $\mathbb Y^{n+1}$
. In the Euclidean case, we take the affine model and write
$\mathbb Y^{n+1}$
. In the Euclidean case, we take the affine model and write
![]() $\mathbb E^{n}=\{ x \in \mathbb E^{n+1} \mid x_{n+1}=0\}$
. In the hyperbolic case, we interpret
$\mathbb E^{n}=\{ x \in \mathbb E^{n+1} \mid x_{n+1}=0\}$
. In the hyperbolic case, we interpret
![]() $\mathbb H^{n}$
as the upper sheet of the hyperboloid in
$\mathbb H^{n}$
as the upper sheet of the hyperboloid in
![]() $\mathbb R^{n+1}$
, that is,
$\mathbb R^{n+1}$
, that is,
where
![]() $\,\langle x,x\rangle _{n,1}\,=x_{1}^{2}+\cdots +x_{n}^{2}-x_{n+1}^{2}$
is the standard Lorentzian form. Its boundary
$\,\langle x,x\rangle _{n,1}\,=x_{1}^{2}+\cdots +x_{n}^{2}-x_{n+1}^{2}$
is the standard Lorentzian form. Its boundary
![]() $\partial \mathbb H^{n}$
can be identified with the set
$\partial \mathbb H^{n}$
can be identified with the set
 $$ \begin{align*} \partial \mathbb H^{n}=\{x\in\mathbb R^{n+1}\mid \,\langle x,x\rangle_{n,1}\,=0\,,\,\sum_{k=1}^{n+1}x_{k}^{2}=1\,,\,x_{n+1}>0\}. \end{align*} $$
$$ \begin{align*} \partial \mathbb H^{n}=\{x\in\mathbb R^{n+1}\mid \,\langle x,x\rangle_{n,1}\,=0\,,\,\sum_{k=1}^{n+1}x_{k}^{2}=1\,,\,x_{n+1}>0\}. \end{align*} $$
In this picture, the isometry group of
![]() $\mathbb H^{n}$
is isomorphic to the group
$\mathbb H^{n}$
is isomorphic to the group
![]() $O^{+}(n,1)$
of positive Lorentzian matrices leaving the bilinear form
$O^{+}(n,1)$
of positive Lorentzian matrices leaving the bilinear form
![]() $\langle \,, \rangle _{n,1}$
and the upper sheet invariant.
$\langle \,, \rangle _{n,1}$
and the upper sheet invariant.
It is well known that each isometry of
![]() $\mathbb X^{n}$
is a finite composition of reflections in hyperplanes, where a hyperplane
$\mathbb X^{n}$
is a finite composition of reflections in hyperplanes, where a hyperplane
![]() $H=H_{v}$
in
$H=H_{v}$
in
![]() $\mathbb X^{n}$
is characterized by a normal unit vector
$\mathbb X^{n}$
is characterized by a normal unit vector
![]() $v \in \mathbb Y^{n+1}$
. Associated to
$v \in \mathbb Y^{n+1}$
. Associated to
![]() $H_{v}$
are two closed half-spaces. We denote by
$H_{v}$
are two closed half-spaces. We denote by
![]() $H^{-}_{v}$
the half-space in
$H^{-}_{v}$
the half-space in
![]() $\mathbb X^{n}$
with outer normal vector v.
$\mathbb X^{n}$
with outer normal vector v.
A (convex) n-polyhedron
![]() $P= \cap _{i\in I} H_{i}^{-} \subset \mathbb X^{n}$
is the non-empty intersection of a finite number of half-spaces
$P= \cap _{i\in I} H_{i}^{-} \subset \mathbb X^{n}$
is the non-empty intersection of a finite number of half-spaces
![]() $H_{i}^{-}$
bounded by the hyperplanes
$H_{i}^{-}$
bounded by the hyperplanes
![]() $H_{i}=H_{v_{i}}$
for
$H_{i}=H_{v_{i}}$
for
![]() $i\in I$
. A facet of P is of the form
$i\in I$
. A facet of P is of the form
![]() $F_{i}=P\cap H_{i}$
for some
$F_{i}=P\cap H_{i}$
for some
![]() $i\in I$
. In the sequel, for
$i\in I$
. In the sequel, for
![]() $\mathbb X^{n} \neq \mathbb S^{n}$
, we always assume that P is of finite volume. In the Euclidean case, this implies that P is compact, and in the hyperbolic case, P is the convex hull of finitely many points
$\mathbb X^{n} \neq \mathbb S^{n}$
, we always assume that P is of finite volume. In the Euclidean case, this implies that P is compact, and in the hyperbolic case, P is the convex hull of finitely many points
![]() $v_{1},\ldots ,v_{k} \in \mathbb H^{n} \cup \partial \mathbb H^{n}$
. If
$v_{1},\ldots ,v_{k} \in \mathbb H^{n} \cup \partial \mathbb H^{n}$
. If
![]() $v_{i} \in \mathbb H^{n}$
, then
$v_{i} \in \mathbb H^{n}$
, then
![]() $v_{i}$
is an ordinary vertex, and if
$v_{i}$
is an ordinary vertex, and if
![]() $v_{i}\in \partial \mathbb H^{n}$
, then
$v_{i}\in \partial \mathbb H^{n}$
, then
![]() $v_{i}$
is an ideal vertex of P, respectively.
$v_{i}$
is an ideal vertex of P, respectively.
If all dihedral angles
![]() $\alpha _{ij}=\measuredangle (H_{i},H_{j})$
formed by intersecting hyperplanes
$\alpha _{ij}=\measuredangle (H_{i},H_{j})$
formed by intersecting hyperplanes
![]() $H_{i}, H_{j}$
in the boundary of P are either zero or of the form
$H_{i}, H_{j}$
in the boundary of P are either zero or of the form
![]() $\frac {\pi }{m_{ij}}$
for an integer
$\frac {\pi }{m_{ij}}$
for an integer
![]() $m_{ij} \geq 2$
, then P is called a Coxeter polyhedron in
$m_{ij} \geq 2$
, then P is called a Coxeter polyhedron in
![]() $\mathbb X^{n}$
. Observe that the Gram matrix
$\mathbb X^{n}$
. Observe that the Gram matrix
![]() $\text {Gr}(P)=(\langle v_{i}, v_{j}\rangle _{\mathbb Y^{n+1}})_{i,j\in I}$
is a real symmetric matrix with
$\text {Gr}(P)=(\langle v_{i}, v_{j}\rangle _{\mathbb Y^{n+1}})_{i,j\in I}$
is a real symmetric matrix with
![]() $1$
’s on the diagonal and non-positive coefficients off the diagonal. In this way, the theory of Perron–Frobenius applies. For further details and references about Coxeter polyhedra in
$1$
’s on the diagonal and non-positive coefficients off the diagonal. In this way, the theory of Perron–Frobenius applies. For further details and references about Coxeter polyhedra in
![]() $\mathbb X^{n}$
, we refer to [Reference Felikson4, Reference Vinberg19, Reference Vinberg20].
$\mathbb X^{n}$
, we refer to [Reference Felikson4, Reference Vinberg19, Reference Vinberg20].
Let
![]() $P= \cap _{i=1}^{N} H_{i}^{-}\subset \mathbb X^{n}$
be a Coxeter n-polyhedron. Denote by
$P= \cap _{i=1}^{N} H_{i}^{-}\subset \mathbb X^{n}$
be a Coxeter n-polyhedron. Denote by
![]() $r_{i}=r_{H_{i}}$
the reflection in the bounding hyperplane
$r_{i}=r_{H_{i}}$
the reflection in the bounding hyperplane
![]() $H_{i}$
of P, and let
$H_{i}$
of P, and let
![]() $G=G_{P}$
be the group generated by
$G=G_{P}$
be the group generated by
![]() $r_{1}, \ldots , r_{N}$
. It follows that G is a discrete subgroup of finite covolume in
$r_{1}, \ldots , r_{N}$
. It follows that G is a discrete subgroup of finite covolume in
![]() $\textrm{Isom}\mathbb X^{n}$
, called a geometric Coxeter group.
$\textrm{Isom}\mathbb X^{n}$
, called a geometric Coxeter group.
A geometric Coxeter group
![]() $G\subset \textrm{Isom}\mathbb X^{n}$
with generating system
$G\subset \textrm{Isom}\mathbb X^{n}$
with generating system
![]() $S=\{r_{1},\ldots ,r_{N}\}$
is the geometric realization of an abstract Coxeter system
$S=\{r_{1},\ldots ,r_{N}\}$
is the geometric realization of an abstract Coxeter system
![]() $(W,S)$
. In fact, we have
$(W,S)$
. In fact, we have
![]() $r_{i}^{2}=1$
and
$r_{i}^{2}=1$
and
![]() $(r_{i}r_{j})^{m_{ij}}=1$
with
$(r_{i}r_{j})^{m_{ij}}=1$
with
![]() $m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$
as above. Here,
$m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$
as above. Here,
![]() $m_{ij}=\infty $
indicates that
$m_{ij}=\infty $
indicates that
![]() $r_{i}r_{j}$
is of infinite order.
$r_{i}r_{j}$
is of infinite order.
For
![]() $\mathbb X^{n}= \mathbb S^{n}$
, G is a spherical Coxeter group and as such finite. For
$\mathbb X^{n}= \mathbb S^{n}$
, G is a spherical Coxeter group and as such finite. For
![]() $\mathbb X^{n}= \mathbb E^{n}$
, G is a Euclidean or affine Coxeter group and of infinite order. By a result of Coxeter [Reference Coxeter3], the irreducible spherical and Euclidean Coxeter groups are entirely classified. In contrast to this fact, hyperbolic Coxeter groups are far from being classified. For a survey about partial classification results, we refer to [Reference Felikson4].
$\mathbb X^{n}= \mathbb E^{n}$
, G is a Euclidean or affine Coxeter group and of infinite order. By a result of Coxeter [Reference Coxeter3], the irreducible spherical and Euclidean Coxeter groups are entirely classified. In contrast to this fact, hyperbolic Coxeter groups are far from being classified. For a survey about partial classification results, we refer to [Reference Felikson4].
For the description of abstract and geometric Coxeter groups, one commonly uses the language of weighted graphs and Coxeter symbols. Let
![]() $(W,S)$
be an abstract Coxeter system with generating system
$(W,S)$
be an abstract Coxeter system with generating system
![]() $S=\{s_{1},\ldots ,s_{N}\}$
and relations of the form
$S=\{s_{1},\ldots ,s_{N}\}$
and relations of the form
![]() $s_{i}^{2}=1$
and
$s_{i}^{2}=1$
and
 $s_{i}s_{j}^{m_{ij}}=1$
with
$s_{i}s_{j}^{m_{ij}}=1$
with
![]() $m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$
. The Coxeter graph of the Coxeter system
$m_{ij}=m_{ji}\in \{2,3,\ldots ,\infty \}$
. The Coxeter graph of the Coxeter system
![]() $(W,S)$
is the non-oriented graph
$(W,S)$
is the non-oriented graph
![]() $\Sigma $
whose nodes correspond to the generators
$\Sigma $
whose nodes correspond to the generators
![]() $s_{1},\ldots ,s_{N}$
. If
$s_{1},\ldots ,s_{N}$
. If
![]() $s_{i}$
and
$s_{i}$
and
![]() $s_{j}$
do not commute, their nodes
$s_{j}$
do not commute, their nodes
![]() $n_{i},n_{j}$
are connected by an edge with weight
$n_{i},n_{j}$
are connected by an edge with weight
![]() $m_{ij}\geq 3$
. We omit the weight
$m_{ij}\geq 3$
. We omit the weight
![]() $m_{ij}=3$
since it occurs frequently. The number N of nodes is the order of
$m_{ij}=3$
since it occurs frequently. The number N of nodes is the order of
![]() $\Sigma $
. A subgraph
$\Sigma $
. A subgraph
![]() $\sigma \subset \Sigma $
corresponds to a special subgroup of
$\sigma \subset \Sigma $
corresponds to a special subgroup of
![]() $(W,S)$
, that is, a subgroup of the form
$(W,S)$
, that is, a subgroup of the form
![]() $(W_{T},T)$
for a subset
$(W_{T},T)$
for a subset
![]() $T\subset S$
. Observe that the Coxeter graph
$T\subset S$
. Observe that the Coxeter graph
![]() $\Sigma $
is connected if
$\Sigma $
is connected if
![]() $(W,S)$
is irreducible.
$(W,S)$
is irreducible.
In the case of a geometric Coxeter group
![]() $G=(W,S)\subset \textrm{Isom}\mathbb X^{n}$
, we call its Coxeter graph
$G=(W,S)\subset \textrm{Isom}\mathbb X^{n}$
, we call its Coxeter graph
![]() $\Sigma $
spherical, affine, or hyperbolic, if
$\Sigma $
spherical, affine, or hyperbolic, if
![]() $\mathbb X^{n}=\mathbb S^{n}, \mathbb E^{n}$
, or
$\mathbb X^{n}=\mathbb S^{n}, \mathbb E^{n}$
, or
![]() $\mathbb H^{n}$
, respectively. In Table 2, we reproduce all the connected affine Coxeter graphs, using the classical notation, with the exception of the three groups
$\mathbb H^{n}$
, respectively. In Table 2, we reproduce all the connected affine Coxeter graphs, using the classical notation, with the exception of the three groups
![]() $\widetilde E_{6}, \widetilde E_{7}, \widetilde E_{8}$
(they will not appear in the following).
$\widetilde E_{6}, \widetilde E_{7}, \widetilde E_{8}$
(they will not appear in the following).
Table 2 Connected affine Coxeter graphs of order
![]() $n+1$
.
$n+1$
.

An abstract Coxeter group with a simple presentation can conveniently be described by its Coxeter symbol. For example, the linear Coxeter graph with edges of successive weights
![]() $k_{1},\ldots ,k_{N}\geq 3$
is abbreviated by the Coxeter symbol
$k_{1},\ldots ,k_{N}\geq 3$
is abbreviated by the Coxeter symbol
![]() $[k_{1},\ldots ,k_{N}]$
. The Y-shaped graph made of one edge with weight p and of two strings of k and l edges emanating from a central vertex of valency
$[k_{1},\ldots ,k_{N}]$
. The Y-shaped graph made of one edge with weight p and of two strings of k and l edges emanating from a central vertex of valency
![]() $3$
is denoted by
$3$
is denoted by
![]() $[p,3^{k,l}]$
(see [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]).
$[p,3^{k,l}]$
(see [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]).
Let us specify the context and consider a Coxeter polyhedron
![]() $P = \cap _{i=1}^{N} H_{i}^{-} \subset \mathbb H^{n}$
. Denote by
$P = \cap _{i=1}^{N} H_{i}^{-} \subset \mathbb H^{n}$
. Denote by
![]() $\Gamma = G_{P} \subset \textrm{Isom}\mathbb H^{n}$
its associated Coxeter group and by
$\Gamma = G_{P} \subset \textrm{Isom}\mathbb H^{n}$
its associated Coxeter group and by
![]() $\Sigma $
its Coxeter graph. Since P is of finite volume, the graph
$\Sigma $
its Coxeter graph. Since P is of finite volume, the graph
![]() $\Sigma $
is connected. Furthermore, if P is not compact, then P has at least one ideal vertex.
$\Sigma $
is connected. Furthermore, if P is not compact, then P has at least one ideal vertex.
Let
![]() $v \in \mathbb H^{n}$
be an ordinary vertex of P. Then, its link
$v \in \mathbb H^{n}$
be an ordinary vertex of P. Then, its link
![]() $L_{v}$
is the intersection of P with a small sphere of center v that does not intersect any facet of P not incident to v. It corresponds to a spherical Coxeter polyhedron of
$L_{v}$
is the intersection of P with a small sphere of center v that does not intersect any facet of P not incident to v. It corresponds to a spherical Coxeter polyhedron of
![]() $ \mathbb S^{n-1}$
and therefore to a spherical Coxeter subgraph
$ \mathbb S^{n-1}$
and therefore to a spherical Coxeter subgraph
![]() $\sigma $
of order n in
$\sigma $
of order n in
![]() $\Sigma $
.
$\Sigma $
.
Let
![]() $v_{\infty } \in \partial \mathbb H^{n}$
be an ideal vertex of P. Then, its link, denoted by
$v_{\infty } \in \partial \mathbb H^{n}$
be an ideal vertex of P. Then, its link, denoted by
![]() $L_{\infty }$
, is given by the intersection of P with a sufficiently small horosphere centered at
$L_{\infty }$
, is given by the intersection of P with a sufficiently small horosphere centered at
![]() $v_{\infty }$
as above. The link
$v_{\infty }$
as above. The link
![]() $L_{\infty }$
corresponds to a Euclidean Coxeter polyhedron in
$L_{\infty }$
corresponds to a Euclidean Coxeter polyhedron in
![]() $\mathbb E^{n-1}$
and is related to an affine Coxeter subgraph
$\mathbb E^{n-1}$
and is related to an affine Coxeter subgraph
![]() $\sigma _{\infty }$
of order
$\sigma _{\infty }$
of order
![]() $\geq n$
in
$\geq n$
in
![]() $\Sigma $
.
$\Sigma $
.
More precisely, if
![]() $v_{\infty }$
is a simple ideal vertex, that is,
$v_{\infty }$
is a simple ideal vertex, that is,
![]() $v_{\infty }$
is the intersection of exactly n among the N bounding hyperplanes of P, the Coxeter graph
$v_{\infty }$
is the intersection of exactly n among the N bounding hyperplanes of P, the Coxeter graph
![]() $\sigma _{\infty }$
is connected and of order n. Otherwise,
$\sigma _{\infty }$
is connected and of order n. Otherwise,
![]() $\sigma _{\infty }$
has
$\sigma _{\infty }$
has
![]() $n_{c}(\sigma _{\infty }) \geq 2$
affine components, and we have the following formula:
$n_{c}(\sigma _{\infty }) \geq 2$
affine components, and we have the following formula:
Recall that a polyhedron is simple if all of its vertices are simple.
As in the spherical and Euclidean cases, hyperbolic Coxeter simplices in
![]() $\mathbb H^{n}$
are all known, and they exist for
$\mathbb H^{n}$
are all known, and they exist for
![]() $n\le 9$
(see [Reference Bourbaki1] or [Reference Vinberg20]). A list of their Coxeter graphs, Coxeter symbols, and volumes can be found in [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]. Among the related Coxeter n-simplex groups, the group
$n\le 9$
(see [Reference Bourbaki1] or [Reference Vinberg20]). A list of their Coxeter graphs, Coxeter symbols, and volumes can be found in [Reference Johnson, Kellerhals, Ratcliffe and Tschantz12]. Among the related Coxeter n-simplex groups, the group
![]() $\Gamma _{n}$
, as given in Table 1, is of minimal covolume.
$\Gamma _{n}$
, as given in Table 1, is of minimal covolume.
The following structural result for simple hyperbolic Coxeter polyhedra due to Felikson and Tumarkin [Reference Felikson and Tumarkin5, Theorem B] will be a corner stone for the proof of our Theorem.
Theorem 2.1 Let
![]() $n \leq 9$
, and let
$n \leq 9$
, and let
![]() $P\subset \mathbb H^{n}$
be a non-compact simple Coxeter polyhedron. If all facets of P are mutually intersecting, then P is either a simplex or isometric to the polyhedron
$P\subset \mathbb H^{n}$
be a non-compact simple Coxeter polyhedron. If all facets of P are mutually intersecting, then P is either a simplex or isometric to the polyhedron
![]() $P_{0}$
whose Coxeter graph is depicted in Figure 1.
$P_{0}$
whose Coxeter graph is depicted in Figure 1.

Figure 1 The Coxeter polyhedron
![]() $P_{0}\subset \mathbb H^{4}$
.
$P_{0}\subset \mathbb H^{4}$
.
2.2 Growth rates and their monotonicity
Let
![]() $(W,S)$
be a Coxeter system and denote by
$(W,S)$
be a Coxeter system and denote by
![]() $a_{k}\in \mathbb Z$
the number of elements
$a_{k}\in \mathbb Z$
the number of elements
![]() $w\in W$
with S-length k. The growth series
$w\in W$
with S-length k. The growth series
![]() $f_{S}(t)$
of
$f_{S}(t)$
of
![]() $(W,S)$
is defined by
$(W,S)$
is defined by
 $$ \begin{align*} f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k}.\end{align*} $$
$$ \begin{align*} f_{S}(t)=1+\sum\limits_{k\ge1}a_{k}t^{k}.\end{align*} $$
In the following, we list some properties of
![]() $f_{S}(t)$
. For references, we refer to [Reference Humphreys11].
$f_{S}(t)$
. For references, we refer to [Reference Humphreys11].
There is a formula due to Steinberg expressing the growth series
![]() $f_{S}(t)$
of a Coxeter system
$f_{S}(t)$
of a Coxeter system
![]() $(W,S)$
in terms of its finite special subgroups
$(W,S)$
in terms of its finite special subgroups
![]() $W_{T}$
for
$W_{T}$
for
![]() $T\subseteq S\,,$
$T\subseteq S\,,$
 $$ \begin{align} \frac{1}{f_{S}(t^ {-1})}=\sum\limits_{{W_{T}<W\atop\scriptscriptstyle{{\vert W_{T}\vert<\infty}}}}\, \frac{(-1)^{\vert T\vert}}{f_{T}(t)}, \end{align} $$
$$ \begin{align} \frac{1}{f_{S}(t^ {-1})}=\sum\limits_{{W_{T}<W\atop\scriptscriptstyle{{\vert W_{T}\vert<\infty}}}}\, \frac{(-1)^{\vert T\vert}}{f_{T}(t)}, \end{align} $$
where
![]() $W_{\varnothing }=\{1\}$
. By a result of Solomon, the growth polynomial of each term
$W_{\varnothing }=\{1\}$
. By a result of Solomon, the growth polynomial of each term
![]() $f_{T}(t)$
in (2) can be expressed by means of its exponents
$f_{T}(t)$
in (2) can be expressed by means of its exponents
![]() $\{m_{1},m_{2},\ldots ,m_{p}\}$
according to the formula
$\{m_{1},m_{2},\ldots ,m_{p}\}$
according to the formula
 $$ \begin{align} f_{T}(t)=\prod\limits_{i=1}^ {p}\,[m_{i}+1], \end{align} $$
$$ \begin{align} f_{T}(t)=\prod\limits_{i=1}^ {p}\,[m_{i}+1], \end{align} $$
where
![]() $\,[k]=1+t+\cdots + t^{k-1}$
and, more generally,
$\,[k]=1+t+\cdots + t^{k-1}$
and, more generally,
![]() $\,[k_{1},\ldots ,k_{r}]:=[k_{1}]\cdots [k_{r}]\,$
. A complete list of the irreducible spherical Coxeter groups together with their exponents can be found in [Reference Kellerhals and Perren14]. For example, the exponents of the Coxeter group
$\,[k_{1},\ldots ,k_{r}]:=[k_{1}]\cdots [k_{r}]\,$
. A complete list of the irreducible spherical Coxeter groups together with their exponents can be found in [Reference Kellerhals and Perren14]. For example, the exponents of the Coxeter group
![]() $\text {A}_{n}$
with Coxeter graph
$\text {A}_{n}$
with Coxeter graph
 are
are
![]() $\{1,2,\ldots ,n\}$
so that
$\{1,2,\ldots ,n\}$
so that
Furthermore, the growth series of a reducible Coxeter system
![]() $(W,S)$
with factor groups
$(W,S)$
with factor groups
![]() $(W_{1},S_{1})$
and
$(W_{1},S_{1})$
and
![]() $(W_{2},S_{2})$
such that
$(W_{2},S_{2})$
such that
![]() $S=(S_{1}\times \{1_{W_{2}}\})\cup (\{1_{W_{1}}\}\times S_{2})$
satisfies the product formula
$S=(S_{1}\times \{1_{W_{2}}\})\cup (\{1_{W_{1}}\}\times S_{2})$
satisfies the product formula
In its disk of convergence, the growth series
![]() $f_{S}(t)$
is a rational function, which can be expressed as the quotient of coprime monic polynomials
$f_{S}(t)$
is a rational function, which can be expressed as the quotient of coprime monic polynomials
![]() $p(t), q(t)\in \mathbb Z[t]$
of the same degree. The growth rate
$p(t), q(t)\in \mathbb Z[t]$
of the same degree. The growth rate
![]() $\tau _{W}=\tau _{(W,S)}$
is defined by the inverse of the radius of convergence of
$\tau _{W}=\tau _{(W,S)}$
is defined by the inverse of the radius of convergence of
![]() $f_{S}(t)$
and can be expressed by
$f_{S}(t)$
and can be expressed by
 $$ \begin{align*} \tau_{W}=\limsup_{k\rightarrow\infty} {a_{k}}^{1/k}. \end{align*} $$
$$ \begin{align*} \tau_{W}=\limsup_{k\rightarrow\infty} {a_{k}}^{1/k}. \end{align*} $$
It is the inverse of the smallest positive real pole of
![]() $f_{S}(t)$
and hence an algebraic integer.
$f_{S}(t)$
and hence an algebraic integer.
Important for the proof of our Theorem is the following result of Terragni [Reference Terragni17] about the growth monotonicity.
Theorem 2.2 Let
![]() $(W,S)$
and
$(W,S)$
and
![]() $(W^{\prime },S^{\prime })$
be two Coxeter systems such that there is an injective map
$(W^{\prime },S^{\prime })$
be two Coxeter systems such that there is an injective map
![]() $ \iota :S\rightarrow S^{\prime } $
with
$ \iota :S\rightarrow S^{\prime } $
with
 $ m_{st} \le m^{\prime }_{\iota (s)\iota (t)}$
for all
$ m_{st} \le m^{\prime }_{\iota (s)\iota (t)}$
for all
![]() $ s,t\in S$
. Then,
$ s,t\in S$
. Then,
![]() $\tau _{(W,S)}\le \tau _{(W^{\prime },S^{\prime })}.$
$\tau _{(W,S)}\le \tau _{(W^{\prime },S^{\prime })}.$
For
![]() $n\geq 2$
, consider a Coxeter group
$n\geq 2$
, consider a Coxeter group
![]() $\Gamma \subset \textrm{Isom}\mathbb H^{n}$
of finite covolume. By results of Milnor and de la Harpe, we know that
$\Gamma \subset \textrm{Isom}\mathbb H^{n}$
of finite covolume. By results of Milnor and de la Harpe, we know that
![]() $\tau _{\Gamma }>1$
. More precisely, and as shown by Terragni [Reference Terragni17],
$\tau _{\Gamma }>1$
. More precisely, and as shown by Terragni [Reference Terragni17],
![]() $ \tau _{\Gamma } \geq \tau _{\Gamma _{9}} \approx 1.1380 $
, where
$ \tau _{\Gamma } \geq \tau _{\Gamma _{9}} \approx 1.1380 $
, where
![]() $\Gamma _{9}$
is the Coxeter simplex group given in Table 1.
$\Gamma _{9}$
is the Coxeter simplex group given in Table 1.
Next, we introduce another tool in the proof of our result, the (simple) extension of a Coxeter graph.
Definition 2.1 Let
![]() $\Sigma $
be an abstract Coxeter graph. A (simple) extension of
$\Sigma $
be an abstract Coxeter graph. A (simple) extension of
![]() $\Sigma $
is a Coxeter graph
$\Sigma $
is a Coxeter graph
![]() $\Sigma ^{\prime }$
obtained by adding one node linked with a (simple) edge to the Coxeter graph
$\Sigma ^{\prime }$
obtained by adding one node linked with a (simple) edge to the Coxeter graph
![]() $\Sigma $
.
$\Sigma $
.
As a direct consequence of Theorem 2.2, if W is a Coxeter group with Coxeter graph
![]() $\Sigma $
, any extension
$\Sigma $
, any extension
![]() $\Sigma ^{\prime }$
of
$\Sigma ^{\prime }$
of
![]() $\Sigma $
encodes a Coxeter group
$\Sigma $
encodes a Coxeter group
![]() $W^{\prime }$
such that
$W^{\prime }$
such that
![]() $\tau _{W}\leq \tau _{W^{\prime }}$
.
$\tau _{W}\leq \tau _{W^{\prime }}$
.
Example 2.3 Consider an irreducible affine Coxeter graph of order
![]() $3$
as given in Table 2. Up to symmetry, the graph
$3$
as given in Table 2. Up to symmetry, the graph
![]() $\widetilde {A}_{2}$
has a unique extension given by the Coxeter graph at the top left in Figure 2. This graph describes the Coxeter tetrahedron
$\widetilde {A}_{2}$
has a unique extension given by the Coxeter graph at the top left in Figure 2. This graph describes the Coxeter tetrahedron
![]() $[3,3^{[3]}]$
of finite volume. The Coxeter graphs
$[3,3^{[3]}]$
of finite volume. The Coxeter graphs
![]() $\widetilde C_{2}$
and
$\widetilde C_{2}$
and
![]() $\widetilde G_{2}$
give rise to the remaining five extensions depicted in Figure 2. By a result of Kellerhals [Reference Kellerhals13], these six Coxeter graphs describe Coxeter tetrahedral groups
$\widetilde G_{2}$
give rise to the remaining five extensions depicted in Figure 2. By a result of Kellerhals [Reference Kellerhals13], these six Coxeter graphs describe Coxeter tetrahedral groups
![]() $\Lambda $
of finite covolume in
$\Lambda $
of finite covolume in
![]() $\textrm{Isom}\mathbb H^{3}$
whose growth rates satisfy
$\textrm{Isom}\mathbb H^{3}$
whose growth rates satisfy
![]() $\tau _{\Lambda }\geq \tau _{\Gamma _{3}}$
.
$\tau _{\Lambda }\geq \tau _{\Gamma _{3}}$
.

Figure 2 Extensions of
![]() $\widetilde A_{2}$
,
$\widetilde A_{2}$
,
![]() $\widetilde C_{2}$
, and
$\widetilde C_{2}$
, and
![]() $\widetilde G_{2}$
.
$\widetilde G_{2}$
.
Example 2.4 In a similar way, any extension of an irreducible affine Coxeter graph of order
![]() $4$
yields a Coxeter simplex group of finite covolume in
$4$
yields a Coxeter simplex group of finite covolume in
![]() $\textrm{Isom}\mathbb H^{4}$
. They are given in Figure 3. Notice that
$\textrm{Isom}\mathbb H^{4}$
. They are given in Figure 3. Notice that
![]() $\Gamma _{4}=[4,3^{2,1}]$
is part of them.
$\Gamma _{4}=[4,3^{2,1}]$
is part of them.

Figure 3 Extensions of
![]() $\widetilde A_{3}$
,
$\widetilde A_{3}$
,
![]() $\widetilde B_{3}$
, and
$\widetilde B_{3}$
, and
![]() $\widetilde C_{3}$
.
$\widetilde C_{3}$
.
Remark 2.5 When considering irreducible affine Coxeter graphs of order greater than or equal to
![]() $5$
, the resulting extensions do not always relate to hyperbolic Coxeter n-simplex groups of finite covolume. For example, among the extensions of
$5$
, the resulting extensions do not always relate to hyperbolic Coxeter n-simplex groups of finite covolume. For example, among the extensions of
![]() $\widetilde {F_{4}}$
, the graph depicted in Figure 4 describes an infinite volume simplex in
$\widetilde {F_{4}}$
, the graph depicted in Figure 4 describes an infinite volume simplex in
![]() $\mathbb H^{5}$
.
$\mathbb H^{5}$
.

Figure 4 An infinite volume
![]() $5$
-simplex.
$5$
-simplex.
3 Proof of the Theorem
Let
![]() $2 \leq n\leq 9$
, and consider the Coxeter simplex group
$2 \leq n\leq 9$
, and consider the Coxeter simplex group
![]() $\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$
whose Coxeter graph is depicted in Table 1. In this section, we provide the proof of our main result stated as follows.
$\Gamma _{n} \subset \textrm{Isom}\mathbb H^{n}$
whose Coxeter graph is depicted in Table 1. In this section, we provide the proof of our main result stated as follows.
Theorem For any
![]() $2 \leq n\leq 9$
, the group
$2 \leq n\leq 9$
, the group
![]() $\Gamma _{n} $
has minimal growth rate among all non-cocompact hyperbolic Coxeter groups of finite covolume in
$\Gamma _{n} $
has minimal growth rate among all non-cocompact hyperbolic Coxeter groups of finite covolume in
![]() $\textrm{Isom}\mathbb H^{n}$
, and as such the group is unique.
$\textrm{Isom}\mathbb H^{n}$
, and as such the group is unique.
For
![]() $n=2$
and for
$n=2$
and for
![]() $n=3$
, the result has been established by Floyd [Reference Floyd6] and Kellerhals [Reference Kellerhals13]. Therefore, it suffices to prove the Theorem for
$n=3$
, the result has been established by Floyd [Reference Floyd6] and Kellerhals [Reference Kellerhals13]. Therefore, it suffices to prove the Theorem for
![]() $4\le n \le 9$
.
$4\le n \le 9$
.
Observe that the growth rates of all Coxeter simplex groups in
![]() $\textrm{Isom}\mathbb H^{n}$
are known. Their list can be found in [Reference Terragni17]. In particular, one deduces the following strict inequalities:
$\textrm{Isom}\mathbb H^{n}$
are known. Their list can be found in [Reference Terragni17]. In particular, one deduces the following strict inequalities:
For a fixed dimension n, one also checks that
![]() $\Gamma _{n}$
has minimal growth rate among (all the finitely many) non-cocompact Coxeter simplex groups
$\Gamma _{n}$
has minimal growth rate among (all the finitely many) non-cocompact Coxeter simplex groups
![]() $\Lambda \subset \textrm{Isom}\mathbb H^{n}$
.
$\Lambda \subset \textrm{Isom}\mathbb H^{n}$
.
As a consequence, we focus on hyperbolic Coxeter groups
![]() $\Gamma \subset \textrm{Isom}\mathbb H^{n}$
generated by at least
$\Gamma \subset \textrm{Isom}\mathbb H^{n}$
generated by at least
![]() $N \geq n+2$
reflections in the facets of a non-compact finite volume Coxeter polyhedron
$N \geq n+2$
reflections in the facets of a non-compact finite volume Coxeter polyhedron
![]() $P\subset \mathbb H^{n}$
. We have to show that
$P\subset \mathbb H^{n}$
. We have to show that
![]() $\tau _{\Gamma _{n}}<\tau _{\Gamma }$
, which yields unicity of the group
$\tau _{\Gamma _{n}}<\tau _{\Gamma }$
, which yields unicity of the group
![]() $\Gamma _{n}$
with this property.
$\Gamma _{n}$
with this property.
Suppose that the Coxeter polyhedron P is simple. By Theorem 2.1, P is either isometric to the polyhedron
![]() $P_{0}\subset \textrm{Isom}\mathbb H^{4}$
depicted in Figure 1, or P has a pair of disjoint facets. For the growth rate
$P_{0}\subset \textrm{Isom}\mathbb H^{4}$
depicted in Figure 1, or P has a pair of disjoint facets. For the growth rate
![]() $\tau $
of the Coxeter group associated to
$\tau $
of the Coxeter group associated to
![]() $P_{0}$
, one easily checks with help of the software CoxIter [Reference Guglielmetti7, Reference Guglielmetti8] that
$P_{0}$
, one easily checks with help of the software CoxIter [Reference Guglielmetti7, Reference Guglielmetti8] that
![]() $\tau _{\Gamma _{4}} <\tau \approx 2.8383 $
. Hence, we can assume that P is not isometric to
$\tau _{\Gamma _{4}} <\tau \approx 2.8383 $
. Hence, we can assume that P is not isometric to
![]() $P_{0}$
. If P has a pair of disjoint facets, then the Coxeter graph
$P_{0}$
. If P has a pair of disjoint facets, then the Coxeter graph
![]() $\Sigma $
of P and its associated group
$\Sigma $
of P and its associated group
![]() $\Gamma $
contains a subgraph
$\Gamma $
contains a subgraph
![]() .
.
The property that the Coxeter graph
![]() $\Sigma $
contains such a subgraph of type
$\Sigma $
contains such a subgraph of type
![]() $\widetilde A_{1} = [\infty ]$
allows us to conclude the proof, whether the polyhedron P is simple or not. In the following, we first look at this property and analyze it more closely.
$\widetilde A_{1} = [\infty ]$
allows us to conclude the proof, whether the polyhedron P is simple or not. In the following, we first look at this property and analyze it more closely.
3.1 In the presence of
 $\widetilde A_{1}$
$\widetilde A_{1}$
We start by considering particular Coxeter graphs of order
![]() $4$
containing
$4$
containing
![]() $\widetilde A_{1}$
. Their related growth rates will be useful when comparing with the one of
$\widetilde A_{1}$
. Their related growth rates will be useful when comparing with the one of
![]() $\Gamma $
. This approach is similar to the one developed in [Reference Bredon and Kellerhals2].
$\Gamma $
. This approach is similar to the one developed in [Reference Bredon and Kellerhals2].
Let
![]() $W_{0} = [\infty ,3,3]$
be the abstract Coxeter group depicted in Figure 5. By means of the software CoxIter, one checks that
$W_{0} = [\infty ,3,3]$
be the abstract Coxeter group depicted in Figure 5. By means of the software CoxIter, one checks that
Figure 5 The Coxeter group
![]() $W_{0}=[\infty ,3,3]$
.
$W_{0}=[\infty ,3,3]$
.
Furthermore, consider the two abstract Coxeter groups
![]() $W_{1}=[3,\infty ,3]$
and
$W_{1}=[3,\infty ,3]$
and
![]() $W_{2}=[\infty , 3^{1,1}]$
given in Figure 6.
$W_{2}=[\infty , 3^{1,1}]$
given in Figure 6.

Figure 6 The Coxeter groups
![]() $W_{1}=[3,\infty ,3]$
and
$W_{1}=[3,\infty ,3]$
and
![]() $W_{2}=[\infty , 3^{1,1}]$
.
$W_{2}=[\infty , 3^{1,1}]$
.
For their growth rates, we prove the following auxiliary result.
Lemma 3.1
![]() $\tau _{W_{0}} < \tau _{W_{1}}$
and
$\tau _{W_{0}} < \tau _{W_{1}}$
and
![]() $ \tau _{W_{0}}< \tau _{W_{2}}$
.
$ \tau _{W_{0}}< \tau _{W_{2}}$
.
Proof For
![]() $0\leq i\leq 2$
, denote by
$0\leq i\leq 2$
, denote by
![]() $f_{i}:=f_{W_{i}}$
the growth series of
$f_{i}:=f_{W_{i}}$
the growth series of
![]() $W_{i}$
and by
$W_{i}$
and by
![]() $R_{i}$
its radius of convergence. Recall that
$R_{i}$
its radius of convergence. Recall that
![]() $R_{i}$
is the smallest positive pole of
$R_{i}$
is the smallest positive pole of
![]() $f_{i}$
, and that
$f_{i}$
, and that
 $\tau _{W_{i}}=\frac 1{R_{i}}$
.
$\tau _{W_{i}}=\frac 1{R_{i}}$
.
We establish the growth functions
![]() $f_{i}$
according to Steinberg’s formula (2). They are given as follows:
$f_{i}$
according to Steinberg’s formula (2). They are given as follows:
 $$ \begin{align*} \begin{array}{lll} \frac{1}{f_{0}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,3]}-\frac1{[2,3,4]} , \\ \\ \frac{1}{f_{1}(t^{-1})}= &1-\frac{4}{[2]}+\frac3{[2,2]} +\frac2{[2,3]}- \frac2{[2,2,3]} , \\ \\ \frac{1}{f_{2}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,2]}-\frac1{[2,3,4]}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} \frac{1}{f_{0}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,3]}-\frac1{[2,3,4]} , \\ \\ \frac{1}{f_{1}(t^{-1})}= &1-\frac{4}{[2]}+\frac3{[2,2]} +\frac2{[2,3]}- \frac2{[2,2,3]} , \\ \\ \frac{1}{f_{2}(t^{-1})}=& 1-\frac{4}{[2]}+\frac3{[2,2]}+\frac2{[2,3]}- \frac1{[2,2,2]}-\frac1{[2,3,4]}. \end{array} \end{align*} $$
Hence, for any
![]() $t>0$
, one has the positive difference functions given by
$t>0$
, one has the positive difference functions given by
 $$ \begin{align*} \begin{array}{lll} \frac1{f_{0}(t^{-1})}-\frac{1}{f_{1}(t^{-1})}&=\frac1{[2,2,3]} - \frac1{[2,3,4]} =\frac{t^{2}+t^{3}}{[2,2,3,4]}> 0 , \\ \\ \frac1{f_{0}(t^{-1})}-\frac{1}{f_{2}(t^{-1})}&=\frac1{[2,2,2]} - \frac1{[2,2,3]} =\frac{t^{2}}{[2,2,2,3]} > 0. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{lll} \frac1{f_{0}(t^{-1})}-\frac{1}{f_{1}(t^{-1})}&=\frac1{[2,2,3]} - \frac1{[2,3,4]} =\frac{t^{2}+t^{3}}{[2,2,3,4]}> 0 , \\ \\ \frac1{f_{0}(t^{-1})}-\frac{1}{f_{2}(t^{-1})}&=\frac1{[2,2,2]} - \frac1{[2,2,3]} =\frac{t^{2}}{[2,2,2,3]} > 0. \end{array} \end{align*} $$
Therefore, for
![]() $i=1,2$
, and for
$i=1,2$
, and for
![]() $u=t^{-1}\in (0,1)$
, the smallest positive root
$u=t^{-1}\in (0,1)$
, the smallest positive root
![]() $R_{0}$
of
$R_{0}$
of
 $\frac 1{f_{0}(u)}$
is strictly bigger than the one of
$\frac 1{f_{0}(u)}$
is strictly bigger than the one of
 $\frac 1{f_{i}(u)}$
. This finishes the proof.
$\frac 1{f_{i}(u)}$
. This finishes the proof.
As a first consequence, combining (5), (7), and Lemma 3.1, one obtains that
for all
![]() $4\leq n \leq 9$
and
$4\leq n \leq 9$
and
![]() $0\le i \le 2$
.
$0\le i \le 2$
.
Next, suppose that the Coxeter graph
![]() $\Sigma $
of
$\Sigma $
of
![]() $\Gamma $
contains a subgraph
$\Gamma $
contains a subgraph
![]() $\widetilde A_{1}$
. Since
$\widetilde A_{1}$
. Since
![]() $\Sigma $
is connected of order
$\Sigma $
is connected of order
![]() $N \geq n+2 \geq 6$
, the subgraph
$N \geq n+2 \geq 6$
, the subgraph
![]() $\widetilde A_{1}$
is contained in a connected subgraph
$\widetilde A_{1}$
is contained in a connected subgraph
![]() $\sigma $
of order
$\sigma $
of order
![]() $4$
in
$4$
in
![]() $\Sigma $
, which is related to a special subgroup W of
$\Sigma $
, which is related to a special subgroup W of
![]() $\Gamma $
. By Theorem 2.2, one has that
$\Gamma $
. By Theorem 2.2, one has that
![]() $\tau _{W_{i}}\leq \tau _{W}$
for some
$\tau _{W_{i}}\leq \tau _{W}$
for some
![]() $0\le i \le 2$
. By combining (8) with these findings, and by Theorem 2.2 and Lemma 3.1, one deduces that
$0\le i \le 2$
. By combining (8) with these findings, and by Theorem 2.2 and Lemma 3.1, one deduces that
This finishes the proof of the Theorem in the presence of a subgraph
![]() $\widetilde A_{1}$
in
$\widetilde A_{1}$
in
![]() $\Sigma $
.
$\Sigma $
.
3.2 In the absence of
 $\widetilde A_{1}$
$\widetilde A_{1}$
Suppose that the Coxeter graph
![]() $\Sigma $
with
$\Sigma $
with
![]() $N\geq n+2$
nodes does not contain a subgraph of type
$N\geq n+2$
nodes does not contain a subgraph of type
![]() $\widetilde A_{1}$
. In particular, by Theorem 2.1, the corresponding Coxeter polyhedron
$\widetilde A_{1}$
. In particular, by Theorem 2.1, the corresponding Coxeter polyhedron
![]() $P \subset \textrm{Isom}\mathbb H^{n}$
is not simple, and it follows that
$P \subset \textrm{Isom}\mathbb H^{n}$
is not simple, and it follows that
![]() $5\le n\le 9$
.
$5\le n\le 9$
.
Consider a non-simple ideal vertex
![]() $v_{\infty }\in P$
. Its link
$v_{\infty }\in P$
. Its link
![]() $L_{\infty } \subset \mathbb E^{n-1}$
is described by a reducible affine subgraph
$L_{\infty } \subset \mathbb E^{n-1}$
is described by a reducible affine subgraph
![]() $\sigma _{\infty }$
with
$\sigma _{\infty }$
with
![]() $n_{c}=n_{c}(\infty )\geq 2$
components which satisfies
$n_{c}=n_{c}(\infty )\geq 2$
components which satisfies
![]() ${ n-1=\text {order}(\sigma _{\infty })-n_{c}}$
by (1). In Table 3, we list all possible realizations for
${ n-1=\text {order}(\sigma _{\infty })-n_{c}}$
by (1). In Table 3, we list all possible realizations for
![]() $\sigma _{\infty }$
by using the following notations.
$\sigma _{\infty }$
by using the following notations.
Let
![]() $\widetilde \sigma _{k}$
be a connected affine Coxeter graph of order
$\widetilde \sigma _{k}$
be a connected affine Coxeter graph of order
![]() $k\geq 3$
as listed in Table 2, and denote by
$k\geq 3$
as listed in Table 2, and denote by
 $\bigsqcup \limits _{k} \widetilde \sigma _{k}$
the Coxeter graph consisting of the components of type
$\bigsqcup \limits _{k} \widetilde \sigma _{k}$
the Coxeter graph consisting of the components of type
![]() $\widetilde \sigma _{k}$
.
$\widetilde \sigma _{k}$
.
Observe that for any graph
 $\bigsqcup \limits _{k} \widetilde \sigma _{k}$
in Table 3, one has
$\bigsqcup \limits _{k} \widetilde \sigma _{k}$
in Table 3, one has
 $3\leq \min \limits _{k} k \leq 5$
, and that the case
$3\leq \min \limits _{k} k \leq 5$
, and that the case
 $\min \limits _{k} k=5$
appears only when
$\min \limits _{k} k=5$
appears only when
![]() $n=9$
.
$n=9$
.
Among the different components of
![]() $\sigma _{\infty }$
, we consider the ones of smallest order
$\sigma _{\infty }$
, we consider the ones of smallest order
![]() $\geq 3$
together with their extensions.
$\geq 3$
together with their extensions.
Table 3 Reducible affine Coxeter graphs
![]() $\sigma _{\infty }$
with
$\sigma _{\infty }$
with
![]() $n_{c}\geq 2$
components
$n_{c}\geq 2$
components
![]() $\widetilde \sigma _{k}$
of order
$\widetilde \sigma _{k}$
of order
![]() $k\geq 3$
such that
$k\geq 3$
such that
![]() $n=\text {order}(\sigma _{\infty })-n_{c}+1$
.
$n=\text {order}(\sigma _{\infty })-n_{c}+1$
.

![]() $\bullet \quad $
Assume that the graph
$\bullet \quad $
Assume that the graph
![]() $\sigma _{\infty }$
of the vertex link
$\sigma _{\infty }$
of the vertex link
![]() $L_{\infty }$
contains an affine component
$L_{\infty }$
contains an affine component
![]() $\widetilde \sigma $
of order
$\widetilde \sigma $
of order
![]() $3$
. By Example 2.3, we know that any extension of
$3$
. By Example 2.3, we know that any extension of
![]() $\widetilde \sigma $
encodes a Coxeter tetrahedral group
$\widetilde \sigma $
encodes a Coxeter tetrahedral group
![]() $\Lambda \subset \textrm{Isom}\mathbb H^{3}$
of finite covolume. The graph
$\Lambda \subset \textrm{Isom}\mathbb H^{3}$
of finite covolume. The graph
![]() $\Sigma $
itself contains a subgraph
$\Sigma $
itself contains a subgraph
![]() $\sigma $
of order
$\sigma $
of order
![]() $4$
which in turn comprises
$4$
which in turn comprises
![]() $\widetilde \sigma $
. The Coxeter graph
$\widetilde \sigma $
. The Coxeter graph
![]() $\sigma $
corresponds to a special subgroup W of
$\sigma $
corresponds to a special subgroup W of
![]() $\Gamma $
, and by Theorem 2.2, we deduce that
$\Gamma $
, and by Theorem 2.2, we deduce that
![]() $\tau _{\Lambda }\leq \tau _{W}$
.
$\tau _{\Lambda }\leq \tau _{W}$
.
Since
![]() $\tau _{\Gamma _{3}}\le \tau _{\Lambda }$
, and in view of (5) and (6), Theorem 2.2 yields the desired inequality
$\tau _{\Gamma _{3}}\le \tau _{\Lambda }$
, and in view of (5) and (6), Theorem 2.2 yields the desired inequality
which finishes the proof in this case, and for
![]() $n=5$
and
$n=5$
and
![]() $n=6$
; see Table 3.
$n=6$
; see Table 3.
![]() $\bullet \quad $
Assume that the graph
$\bullet \quad $
Assume that the graph
![]() $\sigma _{\infty }$
contains an affine component
$\sigma _{\infty }$
contains an affine component
![]() $\widetilde \sigma $
of order
$\widetilde \sigma $
of order
![]() $4$
. We apply the same reasoning as above. By Example 2.4, any extension of
$4$
. We apply the same reasoning as above. By Example 2.4, any extension of
![]() $\widetilde \sigma $
corresponds to a Coxeter 4-simplex group
$\widetilde \sigma $
corresponds to a Coxeter 4-simplex group
![]() $\Lambda $
of finite covolume, and
$\Lambda $
of finite covolume, and
![]() $\tau _{\Gamma _{4}} \leq \tau _{\Lambda }$
. Again,
$\tau _{\Gamma _{4}} \leq \tau _{\Lambda }$
. Again,
![]() $\Sigma $
contains a subgraph
$\Sigma $
contains a subgraph
![]() $\sigma $
comprising
$\sigma $
comprising
![]() $\widetilde \sigma $
. Hence, there exists a special subgroup W of
$\widetilde \sigma $
. Hence, there exists a special subgroup W of
![]() $\Gamma $
described by
$\Gamma $
described by
![]() $\sigma $
so that
$\sigma $
so that
By (10) and (11), the proof is finished in this case, and for
![]() $n=7$
and
$n=7$
and
![]() $n=8$
; see Table 3.
$n=8$
; see Table 3.
![]() $\bullet \quad $
Assume that
$\bullet \quad $
Assume that
![]() $\sigma _{\infty }$
contains an affine component
$\sigma _{\infty }$
contains an affine component
![]() $\widetilde \sigma $
of order
$\widetilde \sigma $
of order
![]() $5$
. By Table 3, one has
$5$
. By Table 3, one has
![]() $7\leq n\leq 9$
. It is not difficult to list all possible extensions of
$7\leq n\leq 9$
. It is not difficult to list all possible extensions of
![]() $\widetilde \sigma $
. There are exactly 15 such extensions. It turns out that there are 11 extensions that encode Coxeter
$\widetilde \sigma $
. There are exactly 15 such extensions. It turns out that there are 11 extensions that encode Coxeter
![]() $5$
-simplex groups of finite covolume, whereas the remaining 4 extensions describe
$5$
-simplex groups of finite covolume, whereas the remaining 4 extensions describe
![]() $5$
-simplex groups
$5$
-simplex groups
![]() $\Delta _{i}, i=1,\ldots ,4,$
of infinite covolume. These last four simplices arise by extending
$\Delta _{i}, i=1,\ldots ,4,$
of infinite covolume. These last four simplices arise by extending
![]() $\widetilde B_{4}$
,
$\widetilde B_{4}$
,
![]() $\widetilde C_{4}$
, and
$\widetilde C_{4}$
, and
![]() $\widetilde F_{4}$
. They are given in Figure 7, together with their associated growth rates computed with CoxIter.
$\widetilde F_{4}$
. They are given in Figure 7, together with their associated growth rates computed with CoxIter.

Figure 7 The Coxeter groups
![]() $\Delta _{i}, i=1,\ldots ,4$
.
$\Delta _{i}, i=1,\ldots ,4$
.
In view of (5), it turns out that
As above, the component
![]() $\widetilde \sigma $
lies in a subgraph
$\widetilde \sigma $
lies in a subgraph
![]() $\sigma $
of order
$\sigma $
of order
![]() $6$
in
$6$
in
![]() $\Sigma $
, and the latter corresponds to a special subgroup W of
$\Sigma $
, and the latter corresponds to a special subgroup W of
![]() $\Gamma $
so that
$\Gamma $
so that
where
![]() $\Lambda $
is a Coxeter
$\Lambda $
is a Coxeter
![]() $5$
-simplex group of finite covolume. Since
$5$
-simplex group of finite covolume. Since
![]() $ \tau _{ \Gamma _{5}} \leq \tau _{\Lambda }$
, and by (5) and (12), one deduces that
$ \tau _{ \Gamma _{5}} \leq \tau _{\Lambda }$
, and by (5) and (12), one deduces that
This finishes the proof of this case.
Finally, all the above considerations allow us to conclude the proof of the Theorem.
Acknowledgment
The author would like to express her gratitude to her supervisor Ruth Kellerhals for all the expert advice and support throughout this project.