Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Gangsong, Leng
and
GuoBiao, Zhou
2002.
Inverse Forms of Hadamard Inequality.
SIAM Journal on Matrix Analysis and Applications,
Vol. 23,
Issue. 4,
p.
990.
Maritz, Pieter
2005.
Sir Thomas Muir, 1844–1934.
Linear Algebra and its Applications,
Vol. 411,
Issue. ,
p.
3.
Akhavi, Ali
Marckert, Jean-François
and
Rouault, Alain
2009.
On the reduction of a random basis.
ESAIM: Probability and Statistics,
Vol. 13,
Issue. ,
p.
437.
Pivovarov, Peter
2010.
On determinants and the volume of random polytopes in isotropic convex bodies.
Geometriae Dedicata,
Vol. 149,
Issue. 1,
p.
45.
Guo, Cali
Li, Hanyang
and
Chen, Shuo
2016.
Study of spectrum sensing exploiting polarization: From optimal LRT to practical detectors.
Digital Signal Processing,
Vol. 49,
Issue. ,
p.
1.
Zheng, Yanpeng
Jiang, Xiaoyu
Chen, Xiaoting
and
Alsaadi, Fawaz
2020.
More extensions of a determinant inequality of Hartfiel.
Applied Mathematics and Computation,
Vol. 369,
Issue. ,
p.
124827.
Xiu, Maxine
Field, Jeff
Bartels, Randy
and
Pezeshki, Ali
2023.
Fisher information and the Cramér–Rao lower bound in single-pixel localization microscopy with spatiotemporally modulated illumination.
Journal of the Optical Society of America A,
Vol. 40,
Issue. 1,
p.
185.


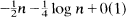 and variance
and variance 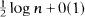 . In particular, for each ε > 0, the probability that
. In particular, for each ε > 0, the probability that 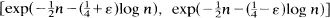 tends to 1 as n tends to ∞.
tends to 1 as n tends to ∞.