Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T06:08:07.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Hook-content Formulae for Symplectic and Orthogonal Tableaux

Published online by Cambridge University Press:  20 November 2018

Peter S. Campbell  and
Anna Stokke
Peter S. Campbell
Affiliation:
e-mail: peter s [email protected]
Anna Stokke
Affiliation:
Department of Mathematics and Statistics, University of Winnipeg, Winnipeg, MB R3B 2E9e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

By considering the specialisation 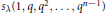${{s}_{\lambda }}(1,\,q,\,{{q}^{2}},\ldots ,\,{{q}^{n-1}})$ of the Schur function, Stanley was able to describe a formula for the number of semistandard Young tableaux of shape $\lambda $ in terms of the contents and hook lengths of the boxes in the Young diagram. Using specialisations of symplectic and orthogonal Schur functions, we derive corresponding formulae, first given by El Samra and King, for the number of semistandard symplectic and orthogonal $\lambda $-tableaux.

Keywords

05E0505E10symplectic tableauxorthogonal tableauxSchur function
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 3 , 01 September 2012 , pp. 462 - 473
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Fulton, W. and Harris, J., Representation theory. A first course. Graduate Texts in Mathematics, 129, Springer-Verlag, New York, 1991.Google Scholar
[2] El Samra, N. and King, R. C., Dimensions of irreducible representations of the classical Lie groups. J. Phys. A 12(1979), no. 12, 2317–2328. http://dx.doi.org/10.1088/0305-4470/12/12/010 Google Scholar
[3] King, R. C., Weight multiplicities for the classical Lie groups. In: Group theoretical methods in physics (Fourth Internat. Colloq., Nijmegen, 1975), Lecture Notes In Physics, 50, Springer, Berlin, 1976, 490–499.Google Scholar
[4] King, R. C. and El-Sharkaway, N. G. I., Standard Young tableaux and weight multiplicities of the classical Lie groups. J. Phys. A 16(1983), no. 14, 3153–3177. http://dx.doi.org/10.1088/0305-4470/16/14/012 Google Scholar
[5] King, R. C. and Welsh, T. A., Construction of orthogonal group modules using tableaux. Linear and Multilinear Algebra 33(1993), no. 3–4, 251–283. http://dx.doi.org/10.1080/03081089308818198 Google Scholar
[6] Koike, K., Principal specializations of the classical groups and q-analogs of the dimension formulas. Adv. Math. 125(1997), no. 2, 236–274. http://dx.doi.org/10.1006/aima.1997.1606 Google Scholar
[7] Proctor, R., Young tableaux, Gel’fand patterns, and branching rules for classical groups. J. Algebra 164(1994), no. 2, 299–360. http://dx.doi.org/10.1006/jabr.1994.1064 Google Scholar
[8] Stanley, R. P., Theory and applications of plane partitions. I, II. Studies in Appl. Math. 50(1971), 167–187; ibid. 259–279.Google Scholar
[9] Stanley, R. P., Enumerative combinatorics. Vol. 2, Cambridge Studies in Advanced Mathematics, 62, Cambridge University Press, Cambridge, 1999.Google Scholar
[10] Sundaram, S., Tableaux in the representation theory of the classical Lie groups. In: Invariant theory and tableaux (Minneapolis, MN, 1988), IMA Vol. Math. Appl., 19, Springer-Verlag, New York, 1990, 191–225.Google Scholar
[11] Sundaram, S., Orthogonal tableaux and an insertion algorithm for SO(2n + 1). J. Combin. Theory Ser. A 53(1990), no. 2, 239–256. http://dx.doi.org/10.1016/0097-3165(90)90059-6 Google Scholar
[12] Weyl, H., The classical groups. Their invariants and representations. Princeton University Press, Princeton, 1939.Google Scholar