Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-21T17:49:57.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Homomorphisms of Lie Algebras of Algebraic Groups and Analytic Groups

Published online by Cambridge University Press:  20 November 2018

Nazih Nahlus
Nazih Nahlus*
Affiliation:
American University of Beirut Beirut, Lebanon
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 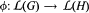be a Lie algebra homomorphism from the Lie algebra of G to the Lie algebra of H in the following cases: (i) G and H are irreducible algebraic groups over an algebraically closed field of characteristic 0, or (ii) G and H are linear complex analytic groups. In this paper, we present some equivalent conditions for ϕ to be a differential in the above two cases. That is, ϕ is the differential of a morphism of algebraic groups or analytic groups as appropriate.

In the algebraic case, for example, it is shown that ϕ is a differential if and only if ϕ preserves nilpotency, semisimplicity, and integrality of elements. In the analytic case, ϕ is a differential if and only if ϕ maps every integral semisimple element of 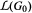into an integral semisimple element of 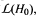, where G0 and H0 are the universal algebraic subgroups of G and H. Via rational elements, we also present some equivalent conditions for ϕ to be a differential up to coverings of G in the algebraic case, and for ϕ to be a differential up to finite coverings of G in the analytic case.

Keywords

17B4522E60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 38 , Issue 3 , 01 September 1995 , pp. 352 - 359
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Hochschild, G., The Structure of Lie Groups, Holden, Day, San Francisco, 1965.Google Scholar
2. Hochschild, G., Basic Theory of Algebraic Groups and Lie Algebras, Graduate Texts in Math. 75, Springer- Verlag, New York, 1981.Google Scholar
3. Hochschild, G. and Mostow, G. D., Representations and representative functions of Lie groups, Ann. of Math. 66(1957), 495–542.Google Scholar
4. Hochschild, G. and Mostow, G. D., Representations and representative functions of Lie groups, II, Ann. of Math. 68(1958), 295–313.Google Scholar
5. Hochschild, G. and Mostow, G. D., Representations and representative functions of Lie groups, III, Ann. of Math. 70(1959), 85—100.Google Scholar
6. Hochschild, G. and Mostow, G. D., On the algebra of representative functions of an analytic group, Amer. J. Math. 83(1961), 111—136.Google Scholar
7. Humphreys, J. E., Algebraic groups and modular Lie algebras, Mem. Amer. Math. Soc. 71(1967).Google Scholar
8. Humphreys, J. E., Introduction to Lie Algebras and Representation Theory, Graduate Texts in Math. 9, Springer-Verlag, New York, 1972.Google Scholar
9. Humphreys, J. E., Linear Algebraic Groups, Graduate Texts in Math. 21, Springer-Verlag, New York, 1975.Google Scholar
10. Nahlus, N., Representative functions on complex analytic groups, Amer. J. Math. 116(1994), 621–636.Google Scholar
11. Seligman, G. B., Algebraic Lie algebras, Bull. Amer. Math. Soc. 74(1968), 1051–1065.Google Scholar
12. Varadarajan, V. S., Lie Groups, Lie Algebras, and Their Representations, Prentice-Hall, Englewood Cliffs, New Jersey, 1974.Google Scholar
13. Waterhouse, W., Introduction to Affine Groups Schemes, Springer-Verlag, New York, 1979.Google Scholar