Hostname: page-component-f554764f5-8cg97 Total loading time: 0 Render date: 2025-04-10T11:27:16.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphic 2-Forms and Vanishing Theorems for Gromov–Witten Invariants

Published online by Cambridge University Press:  20 November 2018

Junho Lee
Junho Lee*
Affiliation:
Department of Mathematics, University of Central Florida, Orlando, FL 32816, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On a compact Kähler manifold 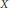$X$ with a holomorphic 2-form $\alpha$, there is an almost complex structure associated with α. We show how this implies vanishing theorems for the Gromov–Witten invariants of 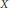$X$. This extends the approach used by Parker and the author for Kähler surfaces to higher dimensions.

Keywords

53D45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 1 , 01 March 2009 , pp. 87 - 94
Copyright
Copyright © Canadian Mathematical Society 2009

References

[B] Behrend, K., The product formula for Gromov–Witten invariants. J. Algebraic Geom. 8(1999), no. 3, 529–541.Google Scholar
[BDL] Bryan, J., Donagi, R., and Leung, N. C., G-bundles on abelian surfaces, hyperkähler manifolds, and stringy Hodge numbers. Turkish J. Math. 25(2001), no. 1, 195–236.Google Scholar
[BHPV] Barth, W., Hulek, K., Peters, C., and de Ven, A. Van, Compact complex surfaces, Second ed., Springer-Verlag, Berlin, 2004.Google Scholar
[BL] Bryan, J. and Leung, N. C., Counting curves on irrational surfaces. In: Surveys in differential geometry: differential geometry inspired by string theory, Surv. Diff. Geom., 5, Int. Press, Boston, MA, 1999, pp. 313–339.Google Scholar
[CN] Camacho, C. and Neto, A. L., Geometric theory of foliations. Birkhäuser Boston, Inc., Boston, MA, 1985.Google Scholar
[CP] Campana, F. and Peternell, T., Complex threefolds with non-trivial holomorphic 2-forms. J. Algebraic Geom. 9(2000), no. 2, 223–264.Google Scholar
[H] Höring, A., Uniruled varieties with split tangent bundle. Math. Z. 256(2007), no. 3, 465–479.Google Scholar
[Ho] Holmann, H., On the stability of holomorphic foliations, Analytic functions, Kozubnik 1979, Lecture Notes in Math. 798, Springer, Berlin, 1980. pp. 192–202.Google Scholar
[HZ] Hori, K., Katz, S., Klemm, A., Pandharipande, R., Thomas, R., Vafa, C., Vakil, R., and Zaslow, E., Mirror symmetry, Clay Mathematics Monographs 1. American Mathematical Society, Providence, RI, Clay Mathematics Institute, Cambridge, MA, 2003.Google Scholar
[L] Lee, J., Family Gromov–Witten Invariants for Kähler Surfaces. Duke Math. J. 123(2004), no. 1, 209–233.Google Scholar
[LP] Lee, J. and Parker, T. H., A structure theorem for the Gromov–Witten invariants of Kähler surfaces. J. Differential Geom. 77(2007), no. 3, 483–513.Google Scholar
[Le] Lehmann, D., Résidues des sous-variétés invariantes d’un feuilletage singulier. Ann. Inst. Fourier 41(1991), no. 1, 211–258.Google Scholar
[LT] Li, J. and Tian, G., Virtual moduli cycles and Gromov–Witten invariants of general symplectic manifolds. Topics in symplectic 4-manifolds, First Int. Press Lect. Ser. I, International Press, Cambridge, MA, 1998, pp. 47–83.Google Scholar