No CrossRef data available.
Article contents
Hölder Continuous Solutions of Degenerate Differential Equations with Finite Delay
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Using known operator-valued Fourier multiplier results on vector-valued Hölder continuous function spaces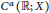 
${{C}^{\alpha }}(\mathbb{R};\,X)$, we completely characterize the 
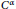${{C}^{\alpha }}$-well-posedness of the first order degenerate differential equations with finite delay 
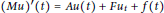$(Mu{)}'(t)\,=\,Au(t)\,+\,F{{u}_{t}}\,+\,f(t)$ for 
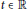$t\,\in \,\mathbb{R}$ by the boundedness of the 
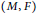$(M,\,F)$-resolvent of A under suitable assumption on the delay operator 
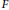$F$, where 
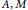$A,M$ are closed linear operators on a Banach space 
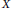$X$ satisfying 
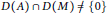$D(A)\,\cap \,D(M)\,\ne \,\{0\}$, the delay operator 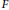$F$ is a bounded linear operator from 
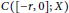$C([-r,0];X)$ to 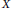$X$, and 
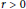$r\,>\,0$ is fixed.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2018
References
[1]
Arendt, W., Batty, C., and Bu., S.
Fourier multipliers for Holder continuous functions and maximal regularity.
Studia Math.
160(2004), no. 1, 23–51.http://dx.doi.Org/10.4064/sm160-1-2
Google Scholar
[2]
Arendt, W., Batty, C., Hieber, M., and Neubrander, F., Vector-valued Laplace transforms and Cauchy Problems.
Monographs in Mathematics, 96, Birkhäuser, Basel, 2001.http://dx.doi.org/10.1007/978-3-0348-5075-9
Google Scholar
[3]
Bourgain, J., A Hausdorff-Young inequality for B-convex Banach Spaces.
Pacific J. Math.
101(1982), no. 2, 255–262.http://dx.doi.org/10.2140/pjm.1982.101.255
Google Scholar
[4]
Bu, S., Well-posedness ofdegenerate differential equations in Holder continuous function Spaces.
Front. Math. China
10(2015), no. 2, 239–248.http://dx.doi.Org/10.1007/s11464-014-0368-4
Google Scholar
[5]
Bu, S., Lp-maximal regularity oj degenerate delay equations with periodic conditions.
Banach J.
Math. Anal.
8(2014), no. 2, 49–59.http://dx.doi.Org/10.15352/bjma/1396640050
Google Scholar
[6]
Carroll, R. W. and Showalter, R. E., Singular and degenerate Cauchy problems.
Mathematics in
Science and Engineering, 127, Academic Press, New York-London, 1976.Google Scholar
[7]
Favini, A. and Yagi, A., Degenerate differential equations in Banach Spaces.
Monographs and
Textbooks in Pure and Applied Mathematics, 215, Dekker, New York, 1999.Google Scholar
[8]
Lizama, C. and Ponce, R., Periodic Solutions oj degenerate differential equations in vector-valued
function Spaces.
Studia Math.
202(2011), no. 1, 49–63.http://dx.doi.Org/10.4064/sm202-1-3
Google Scholar
[9]
Lizama, C., Maximal regularity for degenerate differential equations with infinite delay in periodic vector-valued function Spaces.
Proc. Edinb. Math. Soc. (2)
56(2013), no. 3, 853–871.http://dx.doi.Org/10.1017/S0013091513000606
Google Scholar
[10]
Marinoschi, G., Functional approach to nonlinear modeis of waterflow in soils.
Mathematical Modelling: Theory and Application, 21, Springer, Dordrecht, 2006.Google Scholar
[11]
Pisier, G., Sur les espaces de Banach qui ne contiennent pas uniformément de 
.
C. R. Acad. Sei. Paris Sér. A-B
277(1973), A991–A994.Google Scholar
.
C. R. Acad. Sei. Paris Sér. A-B
277(1973), A991–A994.Google Scholar[12]
Ponce, R., Holder continuous Solutions for Sobolev type differential equations.
Math. Nachr.
287(2014), no. 1, 70–78.http://dx.doi.org/10.1002/mana.201200168
Google Scholar
You have
Access