Hostname: page-component-745bb68f8f-b95js Total loading time: 0 Render date: 2025-01-11T22:33:39.376Z Has data issue: false hasContentIssue false
  • English
  • Français

The Hermite–Joubert Problem and a Conjecture of Brassil and Reichstein

Part of: Diophantine equations Arithmetic algebraic geometry

Published online by Cambridge University Press:  04 January 2019

Khoa Dang Nguyen
Khoa Dang Nguyen*
Affiliation:
Department of Mathematics and Statistics, University of Calgary, 2500 University Drive NW, Calgary, Alberta T2N 1N4 Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that Hermite’s theorem fails for every integer $n$ of the form 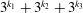$3^{k_{1}}+3^{k_{2}}+3^{k_{3}}$ with integers 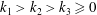$k_{1}>k_{2}>k_{3}\geqslant 0$. This confirms a conjecture of Brassil and Reichstein. We also obtain new results for the relative Hermite–Joubert problem over a finitely generated field of characteristic 0.

Keywords

Hermite–Joubert problemBrassil–Reichstein conjecturediophantine equation

MSC classification

Primary: 11D72: Equations in many variables
Secondary: 11G05: Elliptic curves over global fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 1 , March 2019 , pp. 169 - 177
Copyright
© Canadian Mathematical Society 2018 

References

Bennett, M. A., Effective measures of irrationality for certain algebraic numbers . J. Austral. Math. Soc. Ser. A 62(1997), no.3, 329–344. https://doi.org/10.1017/S144678870000104X.Google Scholar
Bombieri, E. and Gubler, W., Heights in Diophantine geometry . New Mathematical Monographs, 4. Cambridge University Press, Cambridge, 2006. https://doi.org/10.1017/CBO9780511542879.Google Scholar
Brassil, M. and Reichstein, Z., The Hilbert-Joubert problem over p-closed fields . In: Algebraic groups, structure and actions, Proc. Sympos. Pure Math., 94, American Mathematical Society, RI, 2017.Google Scholar
Buhler, J. and Reichstein, Z., On the essential dimension of a finite group . Compositio. Math. 106(1997), 159–179. https://doi.org/10.1023/A:1000144403695.Google Scholar
Coray, D. F., Cubic hypersurfaces and a result of Hermite . Duke Math. J. 54(1987), 657–670. https://doi.org/10.1215/S0012-7094-87-05428-7.Google Scholar
Faltings, G., Diophantine approximation on abelian varieties . Ann. of Math. (2) 133(1991), no. 3, 549–576. https://doi.org/10.2307/2944319.Google Scholar
Faltings, G., The general case of S. Lang’s conjecture . In: Barsotti Symposium in Algebraic Geometry (Abano Terme, 1991), Perspect. Math., 15, Academic Press, San Diego, CA, 1994, pp. 175–182.10.1016/B978-0-12-197270-7.50012-7Google Scholar
Hermite, C., Sur l’invariant du 18 e ordre des formes du cinquième degré et sur le rôle qu’il joue dans la résolution de l’équation du cinquième degré, extrait de deux lettres de M. Hermite á léditeur . J. Reine Angew. Math. 59(1861), 304–305. https://doi.org/10.1515/crll.1861.59.304.Google Scholar
Joubert, P., Sur l’equation du sixième degré . C. R. Acad. Sci. Paris 64(1867), 1025–1029.Google Scholar
Kraft, H., A result of Hermite and equations of degree 5 and 6 . J. Algebra 297(2006), 234–253. https://doi.org/10.1016/j.jalgebra.2005.04.015.Google Scholar
Lang, S., Fundamentals of diophantine geometry. Springer-Verlag, New York, 1983. https://doi.org/10.1007/978-1-4757-1810-2.Google Scholar
McQuillan, M., Division points on semi-abelian varieties . Invent. Math. 120(1995), 143–159. https://doi.org/10.1007/BF01241125.Google Scholar
Reichstein, Z., On a theorem of Hermite and Joubert . Canad. J. Math. 51(1999), 69–95. https://doi.org/10.4153/CJM-1999-005-x.Google Scholar
Reichstein, Z. and Youssin, B., Conditions satisfied by characteristic polynomials in fields and division algebras . J. Pure Appl. Algebra 166(2002), 165–189. https://doi.org/10.1016/S0022-4049(01)00009-3.Google Scholar
Selmer, E. S., The diophantine equation ax 3 + by 3 + cz 3 = 0 . Acta Math. 85(1951), 203–362. https://doi.org/10.1007/BF02395746.Google Scholar
Silverman, J. H., The difference between the Weil height and the canonical height on elliptic curves . Math. Comp. 55(1990), 723–743. https://doi.org/10.2307/2008444.Google Scholar
Silverman, J. H., The Arithmetic of elliptic curves. Second ed., Graduate Texts in Mathematics, 106, Springer, Dordrecht, 2009.Google Scholar
Vojta, P., Integral points on subvarieties of semiabelian varieties. I . Invent. Math. 126(1996), no. 1, 133–181. https://doi.org/10.1007/s002220050092.Google Scholar