Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-23T17:59:23.861Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke Operators on Jacobi-like Forms

Published online by Cambridge University Press:  20 November 2018

Min Ho Lee  and
Hyo Chul Myung
Min Ho Lee
Affiliation:
Department of Mathematics University of Northern Iowa Cedar Falls, IA 50614 USA, e-mail: [email protected]
Hyo Chul Myung
Affiliation:
Korea Institute for Advanced Study and KAIST 207-43 Chunryangri-dong Dongdaemoon-ku Seoul 130-012 Korea, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Jacobi-like forms for a discrete subgroup 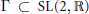$\Gamma \,\subset \,\text{SL}\left( 2,\,\mathbb{R} \right)$ are formal power series with coefficients in the space of functions on the Poincaré upper half plane satisfying a certain functional equation, and they correspond to sequences of certain modular forms. We introduce Hecke operators acting on the space of Jacobi-like forms and obtain an explicit formula for such an action in terms of modular forms. We also prove that those Hecke operator actions on Jacobi-like forms are compatible with the usual Hecke operator actions on modular forms.

Keywords

11F2511F12
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 282 - 291
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Cohen, H., Sums involving the values at negative integers of L functions of quadratic characters. Math. Ann. 217 (1975), 271–285.Google Scholar
[2] Cohen, P., Manin, Y., and Zagier, D., Automorphic pseudodifferential operators. In: Algebraic aspects of nonlinear systems, Birkhäuser, Boston, 1997, 17–47.Google Scholar
[3] Dong, C. and Mason, G., Transformation laws for theta functions. Preprint (math.QA/9903107).Google Scholar
[4] Eichler, M. and Zagier, D., The theory of Jacobi forms. Progress in Math. 55, Birkhäuser, Boston, 1985.Google Scholar
[5] Miyake, T., Modular forms. Springer-Verlag, Heidelberg, 1989.Google Scholar
[6] Rankin, R., The construction of automorphic forms from the derivatives of a given form. J. IndianMath. Soc. 20 (1956), 103–116.Google Scholar
[7] Zagier, D., Modular forms and differential operators. Proc. Indian Acad. Sci. Math. Sci. 104 (1994), 57–75.Google Scholar